6.4.Интегральные оценки качества

Интегральные оценки качества являются интегралами времени от некоторых функций переходного процесса свободной составляющей выходного сигнала или ошибки Эти оценки необходимы для получения общей численной оценки быстродействия, перерегулирования, колебательности и т.д. в переходном режиме работы АС и используются в качестве критериев оптимальности выбора параметров автоматической системы.

Рассматривая некоторую интегральную оценку I как функцию параметров автоматической системы , можно решить задачу оптимизации параметров из условия достижения наилучшего качества системы, например,

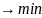) . (6.18)

Интегральные оценки могут быть линейными и квадратичными.

6.4.1.Линейные интегральные оценки

Пусть - составляющая свободного движения координаты в переходном режиме, 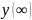- значение выходной координаты в установившемся режиме, тогда простейшей интегральной оценкой качества переходного процесса может служить величина

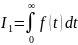, (6.19)

где

Если система устойчива, то 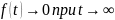и интеграл (6.19) конечен.

Графическая интерпретация этой интегральной оценки представлена на рис. 6.1. Интеграл (6.19) представляет собой сумму площадей, ограниченных кривой переходного процесса и линией , взятых с соответствующим знаком.

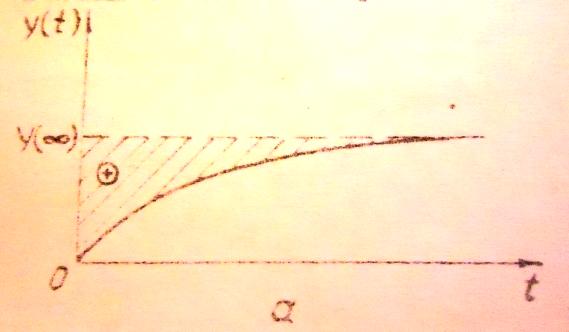
Рис. 6.1

Если на вход автоматической системы подать единичную ступенчатую функцию, то качество переходного процесса можно оценить по интегралу от разности

Очевидно, что чем меньше площадь, ограниченная кривой переходного процесса, тем более предпочтителен переходный процесс.

Величину интегральной оценки I₁ легко определить, так как она связана с изображением функции по Лапласу

(6.20)

Линейная интегральная оценка находит широкое применение только для монотонных переходных процессов (см. рис. 6.1, а), так как в случае колебательного переходного процесса (см. рис. 6.1, б) площади, ограниченные кривой переходного процесса, при расчете интеграла суммируются с разными знаками и малая величина оценки I₁ еще не свидетельствует о хорошем качестве регулирования. Поэтому, когда вид переходного процесса заранее неизвестен, либо имеет колебательный характер, используются интегральные квадратичные оценки.

6.4.2.Интегральные квадратичные оценки

Простейшая интегральная оценка представляет собой интеграл от функции

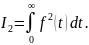(6.21)

Очевидно, что величина будет тем меньше, чем меньше сумма всех площадей переходного процесса, так как знак площади не влияет на величину интеграла (6.21) и чем лучше переходной процесс, тем меньше величина оценки .

Из формулы (6.21) видно, что при использовании данной интегральной оценки качество переходного процесса оценивается только по величине отклонения текущего значения выходной координаты от ее установившегося значения. Однако на практике часто возникает необходимость учитывать и скорость изменения выходной координаты. В этом случае в качестве критерия оптимальности для набора параметров системы используется интегральная квадратичная оценка

, (6.22)

где Т – константа.

Эта интегральная квадратичная оценка может быть представлена в виде

, (6.23)

где .

При необходимости можно создавать интегральные квадратичные оценки более сложной конструкции, например,

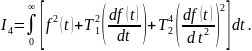(6.24)

Выбор того или иного вида оценок в качестве критерия оптимальности зависит от требований, предъявляемых к качеству системы автоматического регулирования, сложности операций поиска оптимальных параметров системы и различных ограничений конструктивного характера.

Рассмотрим влияние типа интегральной квадратичной оценки на вид переходного процесса в синтезируемой АС.

Пусть параметры , связанные некоторым образом с коэффициентами числителя и знаменателя передаточной функции АС, выбираются из условия (6.18). Тогда, если отсутствуют ограничения на область значений искомых параметров, они определяются из решения системы уравнений

(6.25)

Если имеются ограничения на возможные значения параметров , то уравнения (6.25) решаются методами нелинейного программирования.

Пир использовании в качестве критерия оптимальности интегральной квадратичной оценки I₂ ее минимум I₂=0 при входном воздействии x(t)=1(t) достигается тогда, когда

(6.26)

Следовательно, выбор параметров АС в соответствии с уравнениями (6.25) должен обеспечить максимально возможную скорость отработки входного сигнала. Однако реальные АС не могут обеспечить точное воспроизведение функции (6.26) и вследствие высокой скорости нарастания переднего фронта переходного процесса будет наблюдаться значительное перерегулирование и колебательность. Поэтому использовать квадратичную оценку I₂ целесообразно только в тех случаях, когда требуется высокое быстродействие АС, а перерегулирование и колебательность не играют существенной роли.

В тех случаях, когда перерегулирование или колебательность нежелательны, в качестве критерия оптимальности используется интегральная оценка I₃.

Выражение (6.22) можно представить в виде

(6.27)

откуда следует, что минимум I₃ достигается при

при 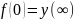. (6.28)

Решение этого дифференциального уравнения имеет вид

(t>0),

откуда

при t>0. (6.29)

Отсюда следует, что идеальным переходным процессом, при котором , является экспонента (6.27). Скорость нарастания экспоненты полностью определяется параметром Т. Следовательно, при выборе параметров АС для обеспечения плавного перехода выходной координаты y(t) к своему установившемуся значению в качестве критерия оптимальности целесообразно использовать интегральную квадратичную оценку I₃.

При использовании интегральной оценки I₄ идеальный переходный процесс определяется решением дифференциального уравнения

(6.30)

Решение этого уравнения представляет собой более сложную функцию, чем экспонента и позволяет при соответствующем подборе параметров Т₁ и Т₂ точнее задать желаемый вид переходного процесса. Однако увеличение сложности интегральных оценок влечет за собой увеличение потребных расчетов при нахождении оптимальных значений параметров. Поэтому при выборе вида критерия оптимальности практически руководствуются конкретными потребностями. Одному и тому же значению интегральной оценки могут соответствовать разные формы переходного процесса.

10