Лекция 6. Методы оценки качества регулирования

6.1.Общие положения

При исследовании линейных автоматических систем решается задача обеспечения требуемых значений показателей качества регулирования: быстродействие, колебательность, перерегулирование и т.д., характеризующих точность и плавность протекания процессов в системе. Как известно, автоматическая система может находиться в переходном или установившемся режимах. В связи с этим различают две группы показателей качества: первая группа – показатели качества переходного процесса; вторая группа – показатели, характеризующие установившуюся составляющую процесса регулирования, по которой определяется точность системы или ошибки системы в установившемся режиме.

Показатели качества, определяемые непосредственно по кривой переходного процесса, называются прямыми оценками качества.

Кривая переходного процесса может быть получена теоретически или экспериментально. Но чаще всего ее нахождение связано с большими трудностями, так как расчет переходного процесса в системах высокого порядка сложен, а эксперимент не всегда осуществим. Поэтому для оценки качества переходного процесса используются косвенные оценки качества, полученные другим путем, не требующим нахождения кривой переходного процесса, например, с помощью интегральных оценок качества.

Ошибки АС в установившемся режиме обусловлены двумя причинами. Первая причина заключается в том, что система неточно отрабатывает задающее воздействие из-за заложенных в ней конструктивных (структурных) принципов. Вторая причина связана с наличием случайных возмущающих воздействий на входе системы.

При анализе качества работы АС в установившемся режиме различают статический и динамический стационарные режимы.

Статический режим – это режим, при котором все внешние воздействия и параметры самой системы не меняются во времени.

Динамический стационарный режим – это режим, при котором внешние воздействия изменяются по некоторому установившемуся закону, а параметры самой системы остаются неизменными. В динамическом стационарном режиме автоматическая система совершает установившиеся вынужденные движения.

В зависимости от вида воздействия различают статическую и динамическую ошибки автоматической системы. Эти ошибки легко определить из формулы:

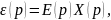_(6.1)

где - изображение по Лапласу ошибки системы;

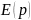- передаточная функция ошибки;

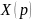- изображение по Лапласу входного сигнала.

Если вместо использовать E_f(p), то формула (6.1) окажется справедливой и для ошибки системы, вызванной возмущающим воздействием.

В статическом режиме входное воздействие

, поэтому

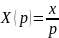
Предположим, что существует предел

, (6.2)

где K_p(p) – передаточная функция разомкнутой системы.

Тогда статическую ошибку можно определить по формуле

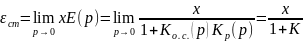. (6.3)

Системы, у которых предел (6.3) отличен от нуля, называются статическими. Они имеют ошибки в установившихся режимах при постоянных входных воздействиях, объясняемые особенностями принципов их действия. Особенности принципов действия АС определяются их структурой и находят свое отражение в передаточных функциях ошибок. Из формул (6.2) и (6.3) видно, что при 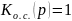величина К есть коэффициент усиления разомкнутой системы, а величина равна отклонению выходного сигнала от задающего воздействия в установившемся режиме. Чем больше коэффициент усиления разомкнутой системы, тем меньше статическая ошибка. Однако величина коэффициента усиления ограничена требованиями к устойчивости и качеству переходных процессов, поэтому статическую ошибку в статической системе нельзя сделать бесконечно малой.

Величину

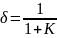(6.4)

обычно называют статизмом автоматической системы.

Если же автоматическая система по принципу своего действия в установившемся режиме не имеет статической ошибки ( ), то она называется астатической.

Динамическая ошибка системы существенно зависит от вида задающего воздействия и в общем случае может быть найдена по формуле

(6.5)

Однако на практике для расчета динамических ошибок удобно использовать более простой метод коэффициентов ошибок.