2.5 Статичні характеристики типових з’єднань елементів
Алгоритмічна структура будь-якої автоматичної системи управління являє собою комбінацію трьох типових з’єднань елементів: послідовної, паралельної і обернено-паралельної дії. Кожне з’єднання може бути за простими правилами замінене одним елементом, статичні і динамічні властивості якого еквівалентні властивостям з’єднання.
При
послідовному з’єднанні (рис. 2.6, а)
вихідна величина кожного попереднього
елемента є вхідною для наступного (і
тільки для нього одного). Якщо елементи
лінійні і в статиці характеризуються
передавальними коефіцієнтами
,
то згідно з визначенням передавального
коефіцієнта можна записати систему
рівнянь
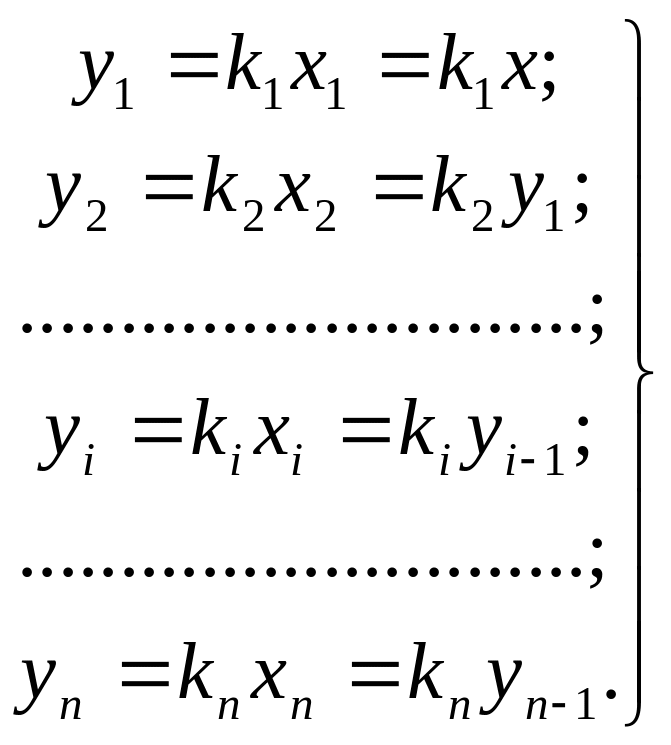(2.65)
Викидаючи
з (2.65) проміжні змінні
,
одержимо рівняння
, (2.66)
з якого випливає, що передавальний коефіцієнт еквівалентного елемента
а – послідовне; б – паралельне; в – зустрічно-паралельне (із зворотним в’язком) Рисунок 2.6 – Типові з’єднання елементів |
. (2.67)
Таким чином, загальний передавальний коефіцієнт послідовно з’єднаних елементів рівний добутку передавальних коефіцієнтів цих елементів. Розмірність загального передавального коефіцієнта рівна добутку розмірностей коефіцієнтів.
Так як при послідовному з’єднанні вихід кожного попереднього елемента є входом наступного, то передавальні коефіцієнти всіх елементів повинні визначатися лінеаризацією статичних характеристик в точках, які відповідають одному і тому ж режиму.
Паралельним з’єднанням називають таке з’єднання, при якому на вхід всіх елементів поступає одна і та ж дія, а їх вихідні величини (з відповідними знаками) підсумовуються (рис. 2.6, б). Згідно з цим визначенням
(2.68)
(2.69)
Підставляючи в (2.69) рівняння статики окремих елементів
(2.70)
одержимо
(2.71)
Звідси випливає, що еквівалентний передавальний коефіцієнт паралельно з’єднаних елементів рівний сумі передавальних коефіцієнтів елементів
. (2.72)
Відзначимо,
що підсумування сигналів
в одній точці можливе лише в тому випадку,
коли вони мають однакову розмірність.
Тому коефіцієнти всіх паралельно
включених елементів і коефіцієнтів
завжди мають одну і ту ж розмірність.
Обернено-паралельним з’єднанням двох елементів (з’єднанням з оберненим зв’язком) називають таке з’єднання, при якому вихідний сигнал першого елемента поступає на вхід другого, а вихідний сигнал другого елемента з вхідним знаком підсумовується з загальним вхідним сигналом (рис. 2.6, в). Перший елемент, в якому напрям подачі сигналу співпадає з напрямом передачі загального сигналу, називають елементом прямого ланцюга. Другий елемент, в якому напрям передачі сигналу протилежний напряму передачі загального сигналу, називають елементом зворотного зв’язку.
Залежно
від знаку сигналу зворотного зв’язку
розрізняють позитивні і негативні
зворотні зв’язки. Якщо сигнал зворотного
зв’язку
підсумовується (на схемі знак “+”) з
загальним вхідним сигналом х, то зворотний
зв’язок є позитивним. Якщо сигнал
зворотного зв’язку віднімається від
загального сигналу (на схемі знак “–“),
то зворотний зв’язок є негативним.
Розглянемо
статичні властивості з’єднання зі
зворотним зв’язком. Нехай елементи
прямого і зворотного зв’язків лінійні
і характеризуються коефіцієнтами
і
.
Тоді згідно з визначенням поняття
“зворотний зв’язок” можна записати
рівняння прямого ланцюга
, (2.73)
зворотного зв’язку
(2.74)
і вузла підсумування
(2.75)
Підставляючи вираз (2.74) в (2.75), а потім вираз (2.75) в (2.73), одержимо рівняння статики всього з’єднання із зворотним зв’язком
. (2.76)
Звідси еквівалентний передавальний коефіцієнт
, (2.77)
де знак “+” відповідає негативному зворотному зв’язку, а знак “–“ – позитивному.
З
виразу (2.77) випливає, що негативний
зворотний зв’язок зменшує еквівалентний
коефіцієнт, а позитивний - збільшує.
Якщо при позитивному зворотному зв’язку
добуток коефіцієнтів
рівний одиниці, то коефіцієнт
зростає до нескінченності.
З’єднання з негативним зворотним зв’язком володіє позитивною (доброю) властивістю: при достатньо великому добутку величина еквівалентного передавального коефіцієнта практично не залежить від коефіцієнта .
Справді,
при
. (2.78)
Ця властивість широко використовується при конструюванні високо стабільних приладів з елементів зі змінними коефіцієнтами.
Оцінимо вплив нестабільності коефіцієнта на спричинені ним зміни вихідної величини в двох випадках: коли елемент прямого ланцюга діє без зворотного зв’язку і коли він охоплений негативним зворотним зв’язком.
Нехай
без зворотного зв’язку деякому
фіксованому значенню
відповідає значення
,
а в з’єднанні із зворотнім зв’язком
таке ж значення
вихідна величина приймає при значенні
вхідної величини, рівному
.
Приріст вихідної величини, який виникає
через зміни коефіцієнта
на величину
,
.
(2.79)
В з’єднанні зі зворотним зв’язком така ж зміна коефіцієнта створить приріст вихідної величини
.
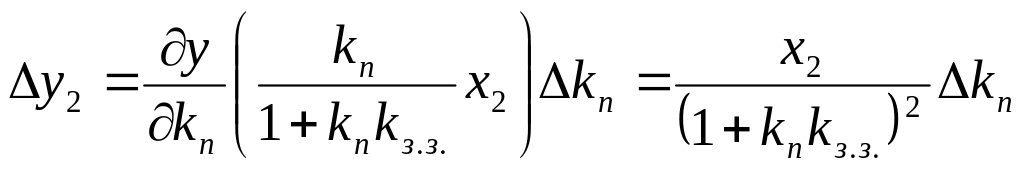(2.80)
Враховуючи
умову вибору значення
,
можна приріст
виразити
через приріст
. (2.81)
Вираз
(2.81) показує, що негативний зворотний
зв’язок зменшує відхилення вихідної
величини, яке виникає через нестабільність
коефіцієнта прямого ланцюга, в
разів.
Приведені викладки ілюструють стабілізуючі дії негативного зворотного зв’язку при параметричному збуренні – при зміні параметра охоплюючої ланки. В главі 6 буде показано, що негативний зворотний зв’язок стабілізує вихідну величину і при координатних збуреннях. Саме дякуючи цьому, негативний зворотний зв’язок лежить в основі всіх замкнутих систем керування.
Розглянемо тепер методи одержання еквівалентних статичних характеристик з’єднань, які складаються з нелінійних елементів. В цьому випадку не можна використовувати формули (2.67), (2.72) і (2.77), еквівалентні характеристики доводиться визначати графічно.
На рис. 2.7 показано, як можна послідовним переносом точок побудувати еквівалентну статичну характеристику послідовного з’єднання трьох елементів з нелінійними характеристиками (рис. 2.7, а).
Рисунок 2.7 – Побудова статичної характеристики послідовного з’єднання елементів |
На рис. 2.8, б показано побудову еквівалентної характеристики паралельного з’єднання трьох нелінійних елементів (рис. 2.8, а). Вихідні сигнали першого і третього елементів підсумовуються, а вихідний сигнал другого – віднімається.
Рисунок 2.8 – Побудова статичної характеристики паралельно з’єднаних елементів |
Тепер
розглянемо зустрічно-паралельне
з’єднання (рис. 2.9, а). В першому квадранті
на рис. 2.9, б побудована характеристика
елемента прямого ланцюга
,
а в другому квадранті – характеристика
елемента зворотного зв’язку
.
Прослідкуємо, як будується еквівалентна
характеристика при негативному зворотному
зв’язку. Задамося деяким фіксованим
значенням y*
вихідної величини і визначимо, чому
повинен дорівнювати вихідний сигнал х
з’єднання. За характеристикою зворотного
зв’язку знаходимо значення y*зз,
яке відповідає значенню y*.
Значення y*зз
сигналу зворотного зв’язку віднімається
від вхідного сигналу, тому значення
вхідного сигналу повинно бути рівне
.
Повторюючи цю процедуру для кількох значень вихідної величини, отримаємо характеристику з’єднання з негативним зворотним зв’язком (лінія 1).
За допомогою аналогічних міркувань і побудови можна отримати еквівалентну характеристику для додаткового зворотного зв’язку (лінія 2).
Рисунок 2.9 – Побудова статичної характеристики елемента, охопленого зворотним зв’язком |
