2.4 Частотні характеристики

Частотні характеристики описують передавальні властивості елементів і систем в режимі встановлених гармонічних коливань, викликаних зовнішніми гармонічними діями. Знаючи частотну характеристику елемента, можна визначити його реакцію на гармонічну дію будь-якої частоти, а також на суму гармонічних дій різної частоти. Частотні характеристики широко використовуються в теорії і практиці автоматичного керування, так як реальні умови, що діють на автоматичні системи, можуть бути представлені як сума гармонічних сигналів. Позитивною властивістю частотних характеристик є те, що вони можуть бути безпосередньо визначені експериментальним шляхом. Розглянемо фізичну сутність і різновид частотних характеристик. Нехай на вхід лінійного елемента (рис. 2.3, а) в момент часу подано гармонічну дію відповідної частоти 

. (2.47)

Через деякий час, необхідний для протікання перехідного процесу (для зникнення вільної складової), елемент ввійде в режим встановлених вимушених коливань, а вихідна величина буде змінюватись за гармонічним законом з тією ж частотою , але з іншою амплітудою і зі зрушенням по осі часу (рис. 2.3, б)

, (2.48)

де – фазове зрушення між вхідним і вихідним сигналами, град.

Повторюючи такий експеримент при фіксуючому для різних значень частоти (від 0 до ), можна встановити, що амплітуда і фазове зрушення  вихідного сигналу конкретного елемента залежать від частоти дії. Подаючи гармонічну дію на вхід різних елементів, можна переконатися, що величини і  залежать також від типу і параметрів елементу. Отже, залежності амплітуди і зрушення  від значень частоти  можуть служити характеристиками динамічних властивостей елементів.

Рисунок 2.3 – Визначення понять частотного методу

Так як амплітуда вихідного сигналу залежить ще від амплітуди вхідного сигналу , то доцільно при описанні передавальних властивостей елементів розглядати відношення амплітуд і .

Залежність відношення амплітуд вихідного і вхідного сигналів від частоти називають амплітудною частотною характеристикою (скорочено АЧХ). Вона позначається . Залежність фазового зрушення між вхідним і вихідним сигналами від частоти називають фазовою частотною характеристикою (ФЧХ) . Можливий вид цих характеристик показаний на рис. 2.4, а і б. Аналітичні вирази і називають відповідно амплітудною і фазовою частотними функціями.

а – амплітудна; б – фазова; в – амплітудно-фазова Рисунок 2.4 – Частотні характеристики

Амплітудна і частотна характеристики показують, як елемент пропускає сигнали різної частоти. Оцінку пропускання виробляють по відношенню амплітуд і . Фазова частотна характеристика показує, яке відставання і випередження вихідного сигналу по фазі створює елемент при різних частотах.

Амплітудна функція має розмірність, рівну відношенню розмірності вихідної величини до розмірності вхідної. В деяких випадках використовують безрозмірну функцію .

Амплітудну і фазову частотні характеристики можна об’єднати в одну загальну – амплітудно-фазову частотну характеристику (АФЧХ). Амплітудно-фазова частотна характеристика являє собою функцію комплексного змінного , модуль якої рівний , а аргумент рівний . Кожному фіксованому значенню частоти відповідає комплексне число , яке на комплексній площині можна зобразити вектором, що має довжину і кут повороту (рис. 2.4, в). Негативні значення , що відповідають відставанню вихідного сигналу від вхідного, прийнято відраховувати за годинниковою стрілкою від позитивного напряму дійсної осі.

При зміні частоти від нуля до нескінченності вектор буде повертатися навколо початку координат, одночасно буде збільшуватися або зменшуватися довжина вектора. Крива, яку при цьому опише кінець вектора, і є амплітудно-фазовою характеристикою. Кожній точці характеристики відповідає відповідне значення частоти. Проекції вектора на дійсну і уявну осі називають відповідно дійсною частотною характеристикою і уявною частотною характеристикою. Позначають їх так: . Зазначимо, що дійсна частотна характеристика завжди парна функція частоти, а уявна характеристика – завжди непарна функція.

Амплітудно-фазова функція , як і будь-яка комплексна величина, може бути представлена в показниковій

(2.49)

або в алгебраїчній формі

. (2.50)

Зв’язок між різними частотними функціями наступний:

, (2.51)

. (2.52)

Аналітичний вираз для амплітудно-фазової характеристики конкретного елемента можна одержати з його передавальної функції підстановкою

. (2.53)

Оскільки амплітудно-фазова функція , як і передавальна функція, являє собою звичайний дріб, то її модуль може бути знайдений за відомим правилом: як відношення модуля чисельника до модуля знаменника:

, (2.54)

а аргумент функції – як різниця аргументів чисельника і знаменника

. (2.55)

Амплітудно-фазова характеристика встановлює зв’язок між вхідним і вихідним сигналами не тільки для випадку, коли вони є гармонічними функціями, але і тоді, коли мають довільний вигляд. Вона рівна відношенню зображення за Фур’є вихідної величини до зображення вхідної величини

. (2.56)

В цьому випадку змінна  змінюється від - до +, так як будь-який реальний сигнал може бути розкладений на суму тільки попарно спряжених векторів, що обертаються.

Користуючись співвідношенням (2.56) та зворотним перетворенням Фур’є, можна встановити зв’язок між частотними і часовими характеристиками. Врахуємо, що при вихідна величина і зображення за Фур’є дельта-функції рівне 1. Тоді імпульсну функцію можна записати так:

. (2.57)

Відповідно амплітудно-фазова функція є зображенням за Фур’є імпульсної перехідної функції

. (2.58)

Так як при функція , то нижня межа інтегрування прийнята рівною нулю.

Якщо (2.58) використати для імпульсної перехідної функції, записаної в безвимірному часі , то амплітудно-фазова характеристика стане функцією безвимірної частоти

, (2.59)

де – масштабний множник, прийнятий за одиницю часу.

Співвідношення (2.59) означає, що якщо розтягувати (стискати) графік функції вздовж осі часу в разів, то графіки амплітудної і фазової характеристик будуть стискатися (розтягуватися) вздовж осі частот  в разів. Ця властивість використовується при побудові безвимірних частотних характеристик і при аналізі зв’язку перехідних процесів з частотними характеристиками систем.

При практичних розрахунках автоматичних систем вигідно використовувати частотні характеристики побудови в логарифмічній системі координат. Такі характеристики називають логарифмічними. Вони мають меншу кривизну і тому можуть бути приблизно замінені ламаними лініями, складеними з декількох прямолінійних відрізків. Причому ці відрізки в більшості випадків вдається побудувати без громіздких обчислень, за допомогою декількох простих правил. Крім того, в логарифмічній системі координат легко знаходити характеристики різних з’єднань елементів, так як множенню і діленню звичайних характеристик відповідають додавання і віднімання ординат логарифмічних характеристик.

За одиницю довжини по осі частот логарифмічних характеристик приймають декаду. Декада – інтервал частот, розташований між самовільним значенням і його десятикратним значенням . Відрізок логарифмічної осі частот, що відповідає одній декаді, рівний 1. Переважно, в розрахунках використовують логарифмічну амплітудно-частотну характеристику (ЛАЧХ)

, (2.60)

ординати якої вимірюють в логарифмічних одиницях – белах або децибелах (скорочено дБ).

Бел – одиниця вимірювання відношення потужностей двох сигналів. Якщо потужність одного сигналу більша (менша) потужності другого сигналу в 10 разів, то ці потужності відрізняються на ( ). Так як потужність гармонічного сигналу пропорційна квадрату його амплітуди, то при використанні цієї одиниці для вимірювання відношення амплітуд перед логарифмом з’являється множник 2. Наприклад, якщо на деякій частоті , то це означає, що потужності вхідного і вихідного сигналів відрізняються в 100² разів, на або на відповідно і .

При побудові фазової частотної характеристики логарифмічний масштаб використовують тільки для осі абсцис.

На рис. 2.5 показані логарифмічна амплітудна характеристика (товста лінія) і відповідна їй наближена характеристика у вигляді прямолінійних відрізків (тонка лінія). Частоти, що відповідають точкам стику відрізків, називають сполучними і позначають .

Правила і приклади побудови наближених логарифмічних характеристик конкретних елементів будуть дані в главі 4.

За видом частотних характеристик всі елементи і системи діляться на дві групи: мінімально-фазові і немінімально-фазові. Мінімально-фазовими є елементи (системи), в яких всі полюси і нулі передавальної функції мають негативні і рівні нулю дійсні частини. Такі елементи дають мінімальний фазовий зсув порівняно з будь-якими іншими елементами, які мають таку саму амплітудну характеристику , але дійсна частина хоча б одного полюса або нуля якої додатна.

Мінімально-фазові елементи володіють цінною для практичних розрахунків властивістю: їх частотна передавальна функція повністю визначається однією з трьох складових: , або . Це істотно полегшує завдання аналізу і синтезу мінімально-фазових систем.

Рисунок 2.5 – Логарифмічна амплітудна частотна характеристика

Приклад. Знайдемо аналітичний вираз для частотних характеристик елемента, передавальна функція якого має вигляд

. (2.61)

Амплітудно-фазова функція елемента

. (2.62)

Вираз для амплітудно-частотної характеристики знайдемо як відношення модулів

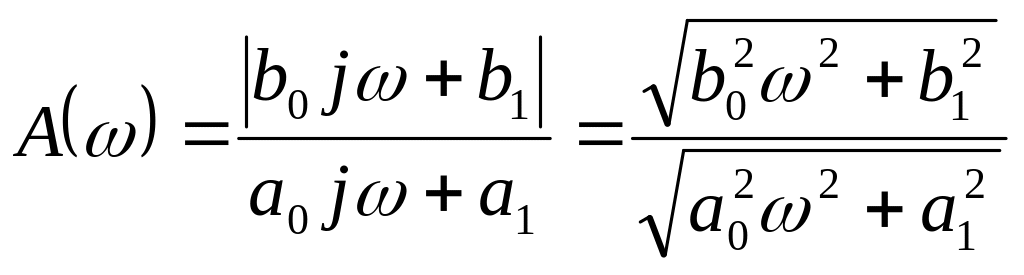, (2.63)

а для фазової – як різницю аргументів чисельника і знаменника

(2.64)