12.5 Синтез модального керування

Якщо багатовимірна АСР синтезована таким чином, що полюси замкнутої АСР мають бажане значення, то говорять про реалізацію модального керування.

Допустимо, що лінеаризована модель об’єкта задана системою рівнянь:

(12.19)

(12.20)

Будемо вважати, що розмірності векторів виходу і керування співпадають і дорівнюють розмірності простору станів, що всі власні числа матриці А дійсні і різні.

Будемо синтезувати керування у вигляді пропорційного зворотнього зв’язку відносно виходів

(12.21)

Відомо, що матрицю можна привести до діагонального вигляду, якщо відома модальна матриця .

, (12.22)

де - діагональна матриця власних чисел.

Співвідношенню (12.22) можна поставити у відповідність інше співвідношення

, (12.23)

Матрицю можна трактувати як ліву, а як праву модальні матриці, т.е. і визначаються як розв’язки векторних рівнянь

(12.24)

(12.25)

Між матрицями і існує таке співвідношення

(12.26)

крім того між матрицями і існує таке співвідношення: і тобто

Рівняння (12.22) і (12.23) можна записати у такому вигляді :

Помноживши перше рівняння останньої рівності на , а друге рівняння на і враховуючи (12.26), отримуємо

(12.27)

(12.28)

Підставляючи і що визначаються рівняннями (12.21) і (12.28) знаходимо

(12.28)

Матрицю виберемо в такому вигляді:

де - діагональна матриця

яку можна розглядати як матричний коефіцієнт підсиленн в колі зворотнього зв’язку. Обчислимо . Якщо тепер матрицю взяти рівною , то рівняння (12.28) набуде такого вигляду :

Оскільки , то . Звідси і

Приймаючи до уваги (12.26), отримуємо

(12.29)

Розв’язок матричного рівняння (12.29) дає

, (12.30)

де - вектор початкових умов;

- фундаментальна матриця замкненої системи.

Оскільки - діагональна матриця, то фундаментальна матриця буде також діагональною з елементами на головній діагоналі.

Враховуючи те, що і відповідно , можемо записати

(12.31)

Рівняння (12.30) або (12.31) показують, що змінюючи можна в бажаному напрямку змінювати власні числа (полючи передавальної функції ) замкнутої системи, при цьому між різними виходами системи немає взаємозв’язку, тобто зміна коефіцієнта підсилення впливає тільки на -й вихід.

Як недолік методу слід відмітити те, що використовується тільки пропорціональні регулятори, матриця спостережень повинна співпадати з матрицею і, як показує практика, це затрудняє на лаштування системи.

Структурна схема модальної АСР показана на рис 12.5.

Рисунок 12.5 Структурна схема модального керування

Якщо розмірність вектора керування менше розмірності вектора керування, то модальне керування можна застосувати до перших власним векторам матриці .

12.6 Поняття про синтез оптимальних регуляторів.

Постановка задачі синтезу. Важливий клас задач синтезу складають так звані лінійні задачі з квадратичним критерієм, розв’язком яких є регулятори зі зворотнім зв’язком. В літературі відповідна методика одержала назву АКОР. Сформулюємо цю задачі.

Нехай модель динаміки керованого об’єкта в просторі станів задається системою

(12.32)

, (12.33)

а рівняння спостереження має такий вигляд

(12.34)

де А,В,С,D – постійні матриці; n-мірний вектор стану керованого об’єкта; -m – мірний вектор керуючих впливів; - k-мірний вектор входу об’єкта (спостереження).

Рівняння (12.34) означає, що вимірюється (спостерігається) - виходів керованого об’єкта, які зв’язані з величинами і співвідношенням (12.34).

Необхідно забезпечити досягнення заданого цільового стану з найменшими можливими втратами. (Пізніше покажемо, що випадок ненульового усталеного значення зводиться до випадку, що розглядається. Шляхом підстановки )

Якість керування визначається квадратичним критерієм

, (12.35)

де і симетричні і додатньо визначені матриці; - час регулювання.

Із виразу (12.35) вилучимо змінну шляхом підстановки її значення із (12.34). Розкриваючи дужки в підінтегральному виразі, отримауємо

(12.36)

де

Матриці і у виразі (12.36) також симетричні, оскільки і .

Поставимо таку задачу. Необхідно знайти таке керування , як функцію фазових координат, яке мінімізувало би критерій якості керування (12.36), задовольняло би диференціальному рівнянню (12.32) і умовам і

Розв’язок задачі синтезу. Розв’язок поставленої задачі ґрунтується на максимізації функції Гамільтона.

, (12.37)

де - підінтегральний вираз критерія синтезу (12.36), - права частина математичної моделі об’єкта, яка записана в матрично векторній формі.

Вектор спряжених змінних обчислюється як розв’язок диференціального рівняння:

(12.38)

З врахуванням значень і рівняння (12.37) набуде такого вигляду

(12.39)

Права частина рівняння (12.38) це градієнт функції за змінною , для знаходження якого скористаємось такими правилами:

де і довільні не нульові вектори розмірністю і ; - матриці.

Останні правила дають можливість знайти

(12.40)

Оскільки на керування не накладено ніяких обмежень, то максимум функції визначається з умови

Враховуючи вираз (12.39) будемо мати

звідси

(12.41)

Якщо в (12.32) підставити одержане значення , то одержимо систему рівнянь

(12.42)

(12.43)

Із (12.41) випливає, що буде функцією змінних стану об’єкта, якщо вибрати в такій формі:

, (12.44)

де - симетрична ( поки що невідома) додатньо визначена матриця розміром .

Продифереціюємо праву і ліву частини рівняння (12.44)

В отримане рівняння замість підставимо його значення, яке визначається правою частиною рівняння (12.42). Крім того врахуємо значення , яке визначається співвідношенням (12.44). В результаті отримуємо

(12.45)

Тепер в праву частину рівняння (12.43) замість і підставимо їх значення, що визначаються рівняннями (12.41) і (12.44), що приводить до такого результату :

(12.46)

В рівняннях (12.45) і (12.46) рівні ліві частини рівнянь, а це означає, що рівними будуть і їх праві частини. Тобто

Після нескладних алгебраїчних перетворень отримаємо

Для того, щоб це рівняння було справедливим для будь-якого значення необхідно перетворення в нуль матричного множника при .

Таким чином, одержуємо рівняння

(12.46)

де

Рівняння (12.46) носить назву матричного рівняння Рік каті.

Отже, оптимальний закон керування зі зворотнім зв’язком за станом об’єкта, або просто оптимальний регулятор, задається виразом

, (12.47)

де матриця знаходиться як розв’язок матричного рівняння Рік каті (12.46)

Система з повним спостереженням. В такому випадку вектор тотожний вектору і відповідно , що спрощує рівняння (12.46)

(12.48)

Відповідно оптимальний регулятор задається виразом

(12.49)

Одномірний об’єкт керування. Його вихід позначимо буквою , а вихід через . Взаємозв’язок між величинами і описується диференціальним рівнянням

Відповідно передавальна функція об’єкта буде мати такий вигляд

(12.50)

де - параметри передавальної функції (постійні величини).

Для реальних об’єктів . Допустимо, що . Якщо це не так, то замінюючи нулями коефіцієнти , приходимо до передавальної функції (12.49).

Отже будемо розглядати передавальну функцію

(12.51)

Передаточній функції (12.50) поставимо у відповідність систему диференціальних рівнянь

(12.52)

Система рівнянь (12.52) еквівалентна передавальній функції (12.50) тому, що виконавши перетворення Лапласа над системою рівнянь (12.52) (при нульових початкових умовах ) і вилучивши із отриманої системи рівнянь всі змінні крім і , отримуємо передавальну функцію (12.51)

Коефіцієнти визначаються як розв’язок системи лінійних рівнянь

(12.53)

Систему рівнянь (12.52) подамо в матрично-векторному вигляді

(12.54)

(12.55)

де

Поставимо задачу синтезу за квадратичним критерієм

(12.56)

де еквівалентні коефіцієнти; - час керування, за умови, що математична модель об’єкта подана у вигляді (12.54), (12.55)

Підставляючи значення із (12.54) в функціонал (12.56), отримуємо

Після очевидних алгебраїчних перетворень будемо мати

Величину , що входить в підінтегральний вираз перетворимо наступним чином:

Отже

(12.57)

де

Отриманий критерій якості керування (12.57) співпадає з (12.36) в якому і .

У відповідності з цим рівняння Ріккаті (12.46) запишиться у такому вигляді

(12.58)

де ;

а алгоритм керування запишемо, використовуючи формулу (12.47)

. (12.59)

Приклад синтезу оптимальної системи керування.

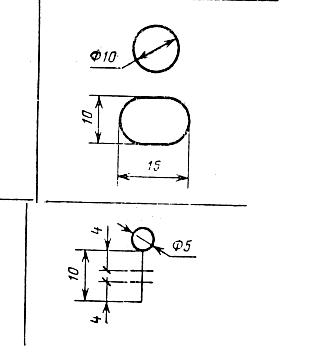
Синтезуємо оптимальний регулятор для об’єкта, який показаний на рис. 12.6.

Р исунок 12.6 Схема керованого об’єкта

Допустимо, що поперечне січення ємності і густина рідини сталі, а інерційністю виконавчого механізму і давача рівня нехтуємо.

Математичну модель об’єкта складемо, виходячи із рівняння матеріального балансу :

, (12.60)

де - статична характеристика виконавчого механізму; - керуючий вплив (вихід регулятора).

Лінеаризована математична модель буде такою

, (12.61)

де ; вихідна координата об’єкта; - збурення, що діє на об’єкт; - керуючий вплив; стала часу об’єкта ,

- передавальні коефіцієнти об’єкта за збуренням і керуючим впливом; індекс “0” вказує на те, що значення відповідних величин відповідає усталеному режиму роботи об’єкта.

Рівнянню (12.61) відповідає та алгоритмічна структура об’єкта, яка показана на рис. 12.7.

Рисунок 12.7 Алгоритмічна структура керованого об’єкта

Об’єкт характеризується двома входами і одним виходом і, відповідно, його динаміка за кожним входом відтворюється двома передавальними функціями.

Синтезуємо оптимальний регулятор, який підтримує постійною величину із умови, що критерій, якій характеризує якість процесу керування має такий вигляд:

(12.62)

де - час керування; і вагові коефіцієнти

Математична модель, яка характеризує динаміку процесу по каналу передачі керуючого впливу має такий вигляд

(12.63)

(12.64)

Допустимо, що

Сформульована задача є задачею синтезу оптимального регулятора для об’єкта з повним спостереженням. Тому алгоритм керування задається співвідношенням (12.49), в якому відповідні матриці слід замінити скалярними величинами і , тобто

(12.65)

Для визначення змінної скористаємось рівнянням Ріккаті (12.48), яке в нашому випадку буде мати такий вигляд:

(12.66)

Ми отримали нелінійне диференціальне рівняння, яке в цьому частковому випадку можна розв’язати аналітичним способом.

Рівняння (12.66) перетворимо наступним чином:

Квадратний тричлен розкладемо на прості множники , де . Тоді

Дріб розкладемо на прості доданки

Тоді

Інтегрування останнього рівняння дає

,

Постійну інтегрування визначимо з умови . Отже

Тепер можемо знайти функцію

(12.66)

Таким чином, оптимальний закон керування для гідравлічного об’єкта (див. рис.12.6) визначається співвідношенням (12.65), де функція визначається згідно рівняння (12.66)

Аналіз алгоритму керування (12.65) показує, що він задає пропорційний регулятор з коефіцієнтом , який є функцією часу .

Якщо прийняти, що , то, як це випливає із рівняння (12.66), за умови, що . В загальному випадку можна записати, що . Тобто, при оптимальний закон керування визначається співвідношенням , де більший із двох коренів квадратичного тричлена

Синтез оптимального ПІ регулятора.

Як ми бачили синтез оптимального регулятора за критерієм (12.35) для лінеаризованого об’єкта проводить до П-алгоритму керування (12.47) з матричним коефіцієнтом підсилення, який є функцією часу . В тому випадку, коли час регулювання коефіцієнт підсилення регулятора прямує до постійної величини і ми отримуємо звичайний П-алгоритм керування, правда, з матричним коефіцієнтом підсилення.

Відомо, що застосування П- регулятора в контурі керування, приводить до статичної похибки, яка в багатьох випадках є небажаною. Тоді як альтернативу П-регулятору застосовують ПІ-регулятор, який в усталеному режимі забезпечує нульову похибку керування.

Синтезуємо оптимальний ПІ регулятор для лінеаризованого об’єкта, математична модель якого – це система векторно-матричних рівнянь (12.32) і (12.34).

Нехай критерій якості процесу керування має такий вигляд

(12.67)

Критерій (12.67) відрізняється від відповідного критерію (12.35) наявністю додаткового множника , де симетрична додатньо визначена матриця розміром , в підінтегральній функції

Візьмемо -мірний вектор , який задовольняє рівняння

(12.68)

Тоді математична модель об’єкта (12.32) і (12.34) набуде такого вигляду :

(12.67)

(12.68)

(12.69)

Визначемо вектор , який носить назву розширеного вектора стану об’єкта . Тоді рівняння (12.67) –(12.69) подамо в такій формі:

Введемо позначення

,

де - блочні матриці, розміри яких відповідно , і . Тоді математичну модель об’єкта можна записати в розширеному просторі станів

(12.70)

(12.71)

Значення , яке визначається рівнянням (12.71) підставимо в (12.67), а другий доданок в підінтегральній функції подамо як квадратичну форму від вектора

де блочна матриця розміром

Отже,

(12.72)

де

В критерій якості керування (12.72) змінна замінена на у відповідності з рівнянням (12.68).

Таким чином, будемо розв’язувати таку задачу.

Керований об’єкт в розширеному просторі станів описується математичною моделлю (12.70), (12.71). Необхідно синтезувати таке оптимальне керування в функції фазових координат , щоб критерій якості керування (12.72) набув найменшого значення.

Порівнюючи між собою структуру задачі (12.32), (12.34) і (12.35) з (12.70) –(12.72) приходимо до висновку, що останнє є задачею синтезу системи з певним спостереженням.

Тому оптимальний алгоритм керування визначається рівнянням яке аналогічне (12.49)

, (12.73)

де блочна матриця розміром і визначається як розв’язок матричного рівняння Ріккаті.

(12.74)

Якщо врахувати, що , де , підматриці блочної матриці , і виконати множення блочних матриць, то

(12.74)

Із рівняння (12.32) визначимо . Для цього помножимо його на матрицію і, якщо існує матриця обернена до матриці , то

Підставляючи значення в (12.74), отримуємо

,

де ,

Інтегруючи останнє рівняння, приходимо до висновку, що

(12.75)

де - значення при .

Таким чином рівняння (12.75) визначає ПІ закон керування, в якому і - матричні коефіцієнти регулятора (матричні параметри регулятора). В тому випадку, коли матриці і прямують до сталих величин і отримуємо звичайний ПІ регулятор

, (12.76)

де і матричні коефіцієнти регулятора.

Додаток А

Таблиця А.1-Графічні позначення приладів, засобів автоматизації та ліній зв’язку згідно ГОСТ 21.404-85

Назва	Позначення
1	2
1. Прилад, що встановлюється поза щитом (по місцю): а) основне позначення б) допустиме позначення
2. Прилад, що встановлюється на щиті, пульті: а) основне позначення б) допустиме позначення
3. Виконавчий механізм. Загальне позначення
4. Виконавчий механізм, який при припиненні подачі енергії чи керуючого сигналу: а) відкриває регулюючий орган б) закриває регулюючий орган в) залишає регулюючий орган в незмінному положенні

Продовження табл.А.1

1	2
­5. Виконавчий механізм з додатковим ручним приводом. Примітка. Позначення може застосовуватись з будь-яким із додаткових знаків, що характе­ризують положення регулюючого органу при припиненні подачі енергії чи керуючого сигналу
6. Лінії зв’язку. Загальне позначення
7. Перетин ліній зв’язку без з’єднання однієї з іншою
8. Перетин ліній зв’язку із з’єднанням між собою

Додаток Б

Таблиця Б.1-Основні буквені позначення вимірювальних величин і функціональних ознак приладів згідно ГОСТ 21.404-85

Поз- наче- ння	Вимірювана величина		Функціональна ознака приладу
	Основне позначе-ння вимірю-вальної	Додаткове позначе-ння, уточ-нююче вимірювану величину	Відобра-ження інфор-мації	Форму-вання сигналу	Додат-кове Значе-ння
1	2	3	4	5	6
А	+	-	Сигналі-зація	-	-
В	+	-	-	-	-
С	+	-	-	Авто- матичне регулю- вання, керува- ння	-
D	Щіль- ність	Різниця, перепад	-	-	-
E	Електри- чна величина	-	+	-	-
F	Витрата	Співвідно- шення, доля, дріб	-	-	-
G	Розмір, положе- ння перемі- щення	-	+	-	-
Н	Ручний вплив	-	-	-	Верхня межа вимі- рюва- ної вели- чини
І	+	-	Покази	-	-

Продовження табл. Б.1

1	2	3	4	5	6
J	+	Автома- тичне пере- ключення, обігання	-	-	-
К	Час, тимчасо- ва програма	-	-	+	-
L	Рівень	-	-	-	Нижня грани- ця вимі- рюва-ної величи- ни
М	Вологість	-	-	-	-
N	+	-	-	-	-
О	+	-	-	-	-
Р	Тиск, вакуум	-	-	-	-
Q	Величи- на харак- теризуюча якість: склад, концерн- трація	Інтегру- вання, сумування по часу	-	+	-
R	Радіо- активність	-	Регі- страція	-	-
S	Швид- кість	-	-	Вклю- чення, відклю- чення, пере- ключе- ння, блоку- вання	-
Т	Темпера- тура	-	-	+	-

Продовження табл. Б.1

1	2	3	4	5	6
U	Кілька різно- рідних вимірю- ваних величин	-	-	-	-
V	В’язкість	-	+	-	-
W	Маса	-	-	-	-
X	Не рекомен- дована резервна буква	-	-	-	-
Y	+	-	-	+	-
Z	+	-	-	+	-

Примітка. Літерні позначення, помічені знаком «+», є резервними, а помічені знаком «—» - не використовуються.

Додаткові літерні позначення, застосовувані для вказівки додаткових функціональних ознак приладів, перетворювачів сигналів і обчислювальних пристроїв, приведені в рекомендованому додатку Б1.

Розміри умовних графічних позначень приладів і засобів автоматизації в схемах приведені і таблиці Б2.

Умовні графічні позначення на схемах виконують суцільною товстою основною лінією, а горизонтальну розділювальну лінію — усередині графічного позначення та лінії зв'язку — суцільною тонкою лінією за ГОСТ 2.303—68.

Таблиця Б.2- Шрифт літерних позначень за ГОСТ 2.304—81 рівним 2,5 мм

Назва	Позначення
Прилад: а)основне позначення б)допустиме позначення
Виконавчий механізм