12.2 Основні властивості об’єктів керування.

На етапі аналізу керованого об’єкта суттєвим є дослідженням його властивостей таких як керованість та спостережливість.

Об’єкт називають керованим, якщо можна знайти таке керування (компоненти якого можуть бути і необмеженими), яке із довільного початкового стану він може бути переведений в кінцевий довільний стан за кінцевий час.

Визначення керованості об’єкта в загальному випадку досить складна задача. Але для лінеаризованих об’єктів, які описуються матричними рівняннями (12.1) коли матриці А і В відомі, можна отримати формальне правило керованості об’єкта.

Для цього необхідно скласти матрицю

, (12.8)

де - розмірність простору станів, і визначити ранг матриці . Об’єкт буде повністю керованим, якщо ранг матриці співпадає з розміром вектора .

Об’єкт називають спостережливим , коли за виміряними значеннями вихідних координат можна визначити змінні стану об’єкта . Оскільки при відомому векторі керування стан об’єкта буде однозначно визначений як розв’язок рівнянь (12.1), коли відоме початкове значення , то об’єкт буде спостережливим, коли за виміряними значеннями можна обчислити складові вектора

Утворимо матрицю

(12.9)

і, якщо ранг цієї матриці дорівнює розмірності вектора стану , то об’єкт називають спостережливим.

12.3 Алгоритмічні структури багатовимірних систем керування.

Розглянемо просту багатовимірну систему керування зі зворотніми зв’язками (рис. 12.1)

В частотній області вихід об’єкта визначається керуючими і збурючими діями у відповідності з виразом:

(12.10)

На схемі (див. рис. 12.1.) показаний також багатовимірний регулятор . Матриця може бути довільною, але на практиці найчастіше матриця діагональна

При цьому елементи , як правило задають стандартні закони керування

АСК, яка показана на рис. 12.1, описується такою системою матричних рівнянь:

(12.11)

,

де - вектор розузгодження; - вектор задаючих дій.

Вилучивши із системи рівнянь (12.11) проміжні змінні і , отримуємо математичну модель замкненої багатовимірної АСК:

або

(12.12)

де - матрична передавальна функція розімкнутої АСК.

Передавальні функції

(12.13)

називають передавальними функціями замкненої АСК за керуванням і збудженням.

12.4 Синтез автоматичних систем керування.

Якість багатовимірних систем керування можна значно поліпшити, якщо застосовувати різні методи компенсації (розв’язування ) перехресних зв’язків. В таких системах зміна якої небудь регульованої величини не приведуть до зміни інших. Системи які мають такі властивості називають автономними. Оскільки в автономних системах досягнута незалежність регульованих величин одна від одної, то такі системи немов би розкладаються на ряд одно контурних незалежних систем керування.

Необхідною і достатньою умовою автономності системи є діагональність матричної передавальної функції.

Нехай необхідно керувати виходами процесу за допомогою керуючої дії . Для цього застосовують багатовимірний регулятор з передавальною функцією , яку здебільшого вибирають діагональною

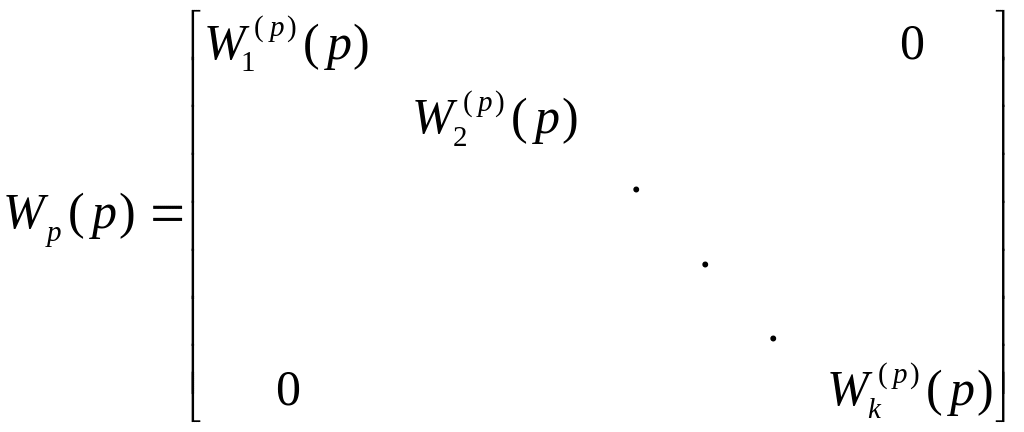
Для компенсації перехресних зв’язків в прямий контур керування після регулятора включаючи компенсатор з передавальною функцією ( рис. 12.2)

Рисунок 12.2 – Багатовимірна система керування з компенсацією перехресних зв’язків (автономна система керування)

Передавальну функцію системи визначимо із такої системи матричних рівнянь:

Якщо із отриманої системи рівнянь виключити всі допоміжні змінні , то отримуємо рівняння динаміки багатовимірної АСК

(12.14)

або (12.15)

Автономність системи буде досягнута, якщо матриця буде діагональною. Очевидно, що автономність в цьому контексті розглядається тільки для квадратних матриць. Якщо число керувань більше числа виходів системи ( > ), то можна вибрати дяку підмножину керувань, яка забезпечує автономність системи. У тому випадку, коли < можлива лише часткова автономність.

Проаналізуємо умови, за яких матриця буде діагональною. Оскільки І діагональна матриця, а сума і добуток діагональних матриць дає діагональну матрицю; крім того операція обернення діагональної матриці не змінює її діагональності, то для діагональності матриці потрібно, щоб матриця була діагональною.

Передавальну матрицю регулятора ми вибрали діагональною. Тому для діагональності необхідно, щоб виконувалась умова

(12.16)

де - діагональна матриця.

Матрицю утворимо із матриці шляхом обнуління її недіагональних елементів, тобто

(12.17)

Тепер рівняння (12.16) набуде такого вигляду:

(12.18)

В автоматичній системі керування, коли компенсатор синтезують у відповідності з (12.18) досягається повна автономність відносно задавленої дії. При цьому залишається вплив кожного збурення на всі виходи системи. Для компенсації цих збурень можна синтезувати комбіновану АСР, в якій використовуються додаткові зв’язки для усунення дії складових вектора на виходи системи .

Приклад 12.2 Синтезуати автономну систему керування для об’єкта, який показаний на рис. 12.3

Р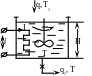 исунок 12.3 – Принципова схема керованого об’єкта

Виходами об’єкта є температура води Т і рівень в ємності Н. Керуючі впливи – витрата рідини , що поступає в ємність; струм І, який протікає через нагрівник.

Складаємо математичну модель об’єкта, використавши рівняння матеріального та теплового балансів.

Рівняння матеріального балансу приводить до диференціального рівняння

,

яке описує зміну рівня в ємності.

На основі рівняння теплового балансу, отримуємо

,

де - площа поперечного перерізу;

- густина рідини;

- теплоємність рідини;

- опір нагрівника;

- місцевий гідравлічний опір.

Будемо вважати, що температура , з якою рідина поступає в ємність постійна. Тоді лінеаризована модель об’єкта набуде такого вигляду:

де

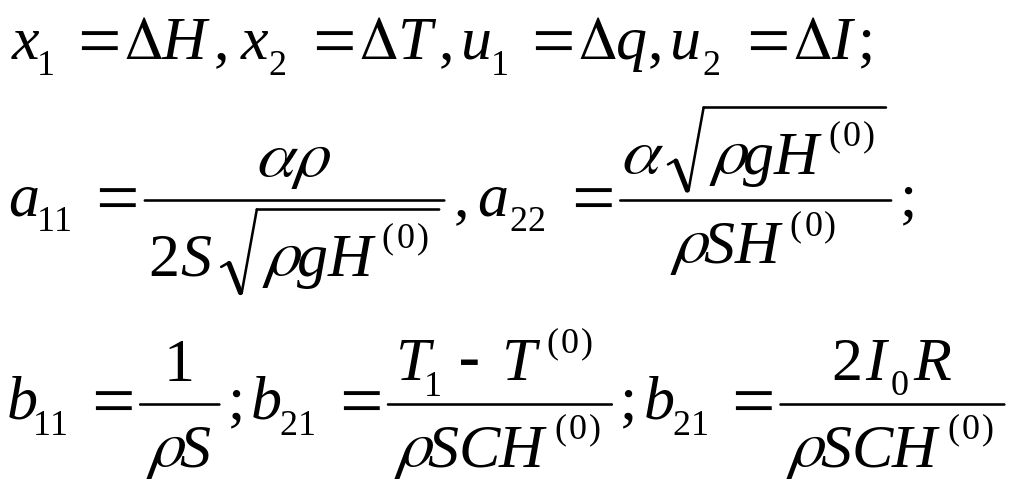
Передавальну функцію об’єкта обчислимо за формулою (12.4) Оскільки , то

;

У відповідності з останньою формулою отримуємо

Відповідно

і

Оскільки

де , то

Структурна (алгоритмічна) схема автономної АСР показана на рис. 12.4

Рисунок 12.4 – Структурна (алгоритмічна) автоматична АСР

У відповідності з формулою (12.14) передавальна функція автономної АСР буде такою:

або враховуючи значення матриць і , отримуємо

Тобто автономна АСР розкладається на дві одно контурні автоматичні системи керування з передавальними функціями

,

Реалізація системи автономного керування наштовхується на ряд труднощів основні з них це:

1. наявність частотного запізнення в контурі керування. Тоді динамічний компенсатор повинен включати елементи випередження які повині визначати майбутні значення виходів

2. Необхідність мати досить точну матеріальну модель об’єкта (передавальну матрицю). Як правило, замість точної моделі передавальної функції використовують її наближення. Якщо точна і наближена передавальні функції об’єкта значно відрізняються між собою, то якість регулювання буде поганою, а система може стати навіть не стійкою

3. Присутність в правих нулів передавальної функції. Ці нулі можуть стати правими полюсами і їх неточна компенсація приводить до того, що в передавальній функції замкненої системи з’являються нестійки полюси, в результаті чого система стає нестійкою.