12. Cтруктурний синтез багатовимірних систем керування (детерміновані системи)

12.1 Математична модель багатовимірної системи керування.

Однією із найбільш типових задач керування є синтез багатовимірної системи керування. Якщо розглядається лінеаризована математична модель технологічного процесу, то її можна подати у вигляді системи матричних рівнянь

(12.1)

де - n-мірний вектор стану; -m-вектор керуючих дій; -к-вектор вихідних величин; - матриця розміром n x n, яка складена із коефіцієнтів при змінних ; - матриця n x m, яка складена із коефіцієнтів при керуючих впливах ; n x d матриця складена із коефіцієнтів при збуреннях , - k x n матриця спостережень.

Рівняння (12.1) описують динаміку лінеаризованого об’єкта в просторі станів.

Другим еквівалентним способом опису динаміки об’єкта при малих відхиленнях є подання математичної моделі в частотній області. Для цього застосовується перетворення Лапласа до системи рівнянь (12.1). У випадку нульових початкових умов маємо

(12.2)

Із першого рівняння системи (12.2) знаходимо

Підставляючи значення в друге рівняння системи (12.2) знаходимо

(12.3)

Якщо через і позначити матричні передавальні функції, які зв’язують керування і збурення з виходом , то отримаємо

, (12.4)

де

,

,

Оскільки одині методи синтезу автоматичних систем керування простіше реалізуються в часовій області, а інші в частотній, то дослідник повинен вміти швидко переходити від одного подання до іншого.

Перехід від подання (12.1) до подання (12.4) єдине і здійснюється воно з використанням перетворення Лапласа. Зворотній перехід від часового подання значно складний. Це пояснюється наступними причинами :

1. Зворотній перехід не єдиний, так як в загальному випадку подання в просторі станів вміщує більше інформації ніж просто матрична передавальна функція;

2. Із всіх можливих систем в просторі станів, які відповідають заданій передавальній функції чи вибирають мінімальну реалізацію, тобто систему з мінімальним розміром в просторі станів, хоча, і в цьому випадку незначність переходу залишається.

Допустимо, що матриця має полюси . Розкладемо матричну передавальну функцію на прості :

, (12.5)

де - матричні лишки в полюсах функцій ( - k x m мірна матриця ), які задаються співвідношенням

, (12.6)

Якщо - ранг матриці , то розмірність простору станів мінімальної реалізації є:

(12.7)

Матрицю будемо шукати у вигляді квазідіагональної матриці

, де - діагональні субматриці, - одинична матриця розмірності .

Співставляючи рівняння (12.5) з виразом передавальної функції

і враховуючи, те, що діагональна матриця породжує діагональну матрицю , можна показати, що

, (12.8)

де - вектор розмірності к; - вектор розмірності m.

Рівняння (12.8) дає змогу визначити матриці і

;

Якщо необхідно визначити матрицю , то матрицю подають у вигляді :

(12.9)

Матричні лишки задаються виразами:

(12.10)

Тоді матриця утворюється із векторів :

Приклад 12.1. Матрична модель об’єкта подана у частотній області

,

де

,

.

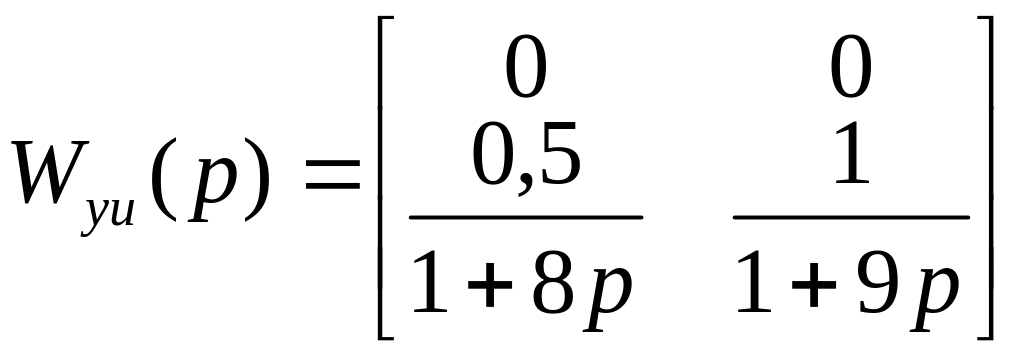Записати математичну модель об’єкта в просторі станів

У відповідності з (12.5) розкладаємо матрицю на елементарні дроби. Для цього обчислимо .

Відповідно

Отже

Ранг матриці дорівнює , а матриці . Мінімальна розмірність простору станів

Матриці і подамо у вигляді співвідношеня (12.8)

,

Тепер можемо записати матриці і

Аналогічно цьому знаходимо подання для матриці Г. Знаходимо, що

,

,

,

Отже,

Г

Таким чином, математична модель об’єкта в просторі станів буде такою

з визначеними нами матрицями А,В і Г