10.4 Дискретна передавальна функція цифрових коректуючих ланок

КМЕОМ, які входять до складу контуру керування можуть бути використані для програмної реалізації коректуючих алгоритмів в ЦСАК. Програмну реалізацію такого алгоритму можна представити у вигляді дискретної передавальної функції (ДПФ)

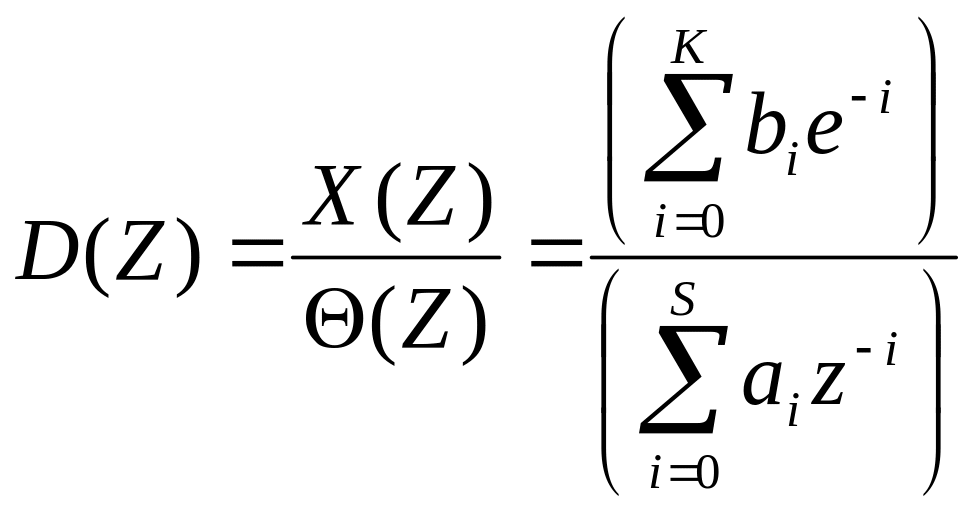(10.10)

де

функції (1) відповідає різницеве рівняння:

(10.11)

Для розв’язання різницевих рівнянь придатними є три методи програмування: прямий, послідовний, паралельний. Кількість операцій при прямому програмуванні становить:

де l і k - відповідно степені лівої та правої частини рівняння (10.11).

Метод прямого програмування використовують тоді, коли ДПФ цифрового обчислювального пристрою має деякі сталі коефіцієнти, що дорівнюють нулю. При цьому запізнення, що вноситься цим методом зводиться до мінімуму.

При послідовному програмуванні кількість операцій дорівнює:

тобто є меншою ніж у прямого програмування.

Загальна кількість операцій при паралельному програмуванні:

В ряді випадків для використання переваг кожного із методів програмування обчислювального пристрою будують з одночасним використанням двох або трьох методів.

Розглянемо можливі варіанти ДПФ коректуючих ланок у ЦСАК:

• ПІД (пропорційно-інтегродиференціальний) алгоритм керування коректуючих ланок.

Якщо у рівняння (10.10) покласти k=2, =1, то ДПФ алгоритму керування матиме вигляд

(10.12)

Різницеве рівняння, що відповідає (10.12) можна записати так:

(10.13)

У (4) відповідає наступній ПІД коректуючий алгоритм керування:

(10.14)

Т_і, Т_g – сталі часу відповідно інтегрування і диференціювання.

Для малих значень періоду дискретизації Т, та реалізації алгоритму інтегрування методом простої різниці інтегральне рівняння (10.13) можна записати у вигляді різницевого рівняння:

n=1

(10.15)

n=n-1

(10.16)

На підставі рівняння (10.15) знаходимо рекурентну формулу для ПІД коректуючого алгоритму керування.

(10.17)

Як бачимо для малих значень Т різницеве рівняння (10.13) ДПФ (10.12) збігається з коректуючим алгоритмом (10.17). Значення коефіцієнтів b₁, b₂, вибирають із умови реалізації потрібних значень Т_g, Т_i та Т.

- ПІ (пропорційно-інтегральний) (ізодромний) коректуючий алгоритм керування.

Якщо в (1)поставити s=1, k=1, a₁=1, то ДПФ коректуючого алгоритму, керування буде мати наступний вигляд:

(10.18)

Різницеве рівняння, що описує (10.18) є рівняння виду:

(10.19)

Рівняння (10) відповідає такому неперервному коректуючому алгоритму:

(10.20)

Для малих значень Т та при реалізації алгоритму інтегрування методом прямокутників, рівняння (10.20) можна записати у вигляді різницевого рівняння.

(10.21)

n=n-1

(10.22)

Щоб сформулювати рекурентне різницеве рівняння від (10.21) віднімемо (10.22)

(10.23)

На підставі (10.23) знаходимо рекурентну формулу пропорційного інтегрального коректуючого алгоритму

(10.24)

де к₀ – коефіцієнт пропорційності.

Як бачимо для малих значень Т рівняння (10.19) ПФ (10.18) збігається з (10.24). Значення коефіцієнтів і вибирається із умови реалізації потрібного значення Т_і, Т.

- І (інтегральний) коректуючий алгоритм керування.

Якщо в (10.10) покласти s=1, k=1, b₀=1, то ДПФ для коректуючого алгоритму керування буде мати наступний вигляд:

(10.25)

Різницеве рівняння, що описує цю функцію має вигляд

(10.26)

Рівняння (10.26) відповідає такому неперервному коректуючому алгоритму

(10.27)

Для малих значень Т та при реалізації алгоритму інтегрування методом прямокутників рівняння (10.27) можна записати у вигляді різницевого рівняння

n=1

(10.28)

n=n-1

(10.29)

Щоб сформулювати рекурентне різницеве рівняння від (10.28) віднімемо (10.29), тоді:

(10.30)

На підставі рівняння (10.30) знаходимо рекурентну формулу І коректуючого алгоритму

(10.31)

- П (пропорційний алгоритм керування).

Якщо в рівняння (10.10) підставити a_і=0, b_i=0, то ДПФ коректуючого алгоритму керування буде мати наступний вигляд:

D(Z)=b_o (10.32)

Різницеве рівняння, що описує цю функцію має вигляд

(10.33)

b_o=1 відповідає одиничному коефіцієнту передачі КМЕОМ.

При b_o1 сигнал підсилюється, при b_o<1 – послаблюється.

- ПД (пропорційно-диференціальний) коректуючий алгоритм керування.

Якщо в рівняння (10.10) покласти s=0, k=1, то ДПФ коректуючого алгоритму керування буде мати вигляд:

D(Z)=b_o+b₁Z^-1 (10.34)

А різницеве рівняння, яке описує цю функцію:

(10.35)

Різницевому рівнянні буде відповідати такий неперервний алгоритм:

(10.36)

Для малих значень періоду дискретизації Т, та при реалізації алгоритму диференціювання методом простої різниці диференційного рівняння (10.36) для такту [n] можна записати у вигляді різницевого рівняння:

(10.37)

Для малих значень Т, різницевого рівняння (10.35) ДПФ (10.34) збігається із коректуючим алгоритмом (10.37). Значення коефіцієнтів та вибирають із умови реалізації потрібних значень постійної диференціювання Т_g та кроку дискретизації Т.

- IД (інтегрально-диференціальний) коректуючий алгоритм керування.

Якщо в рівняння (1) покласти s=1, k=1, то ДПФ коректуючого алгоритму керування буде мати вигляд:

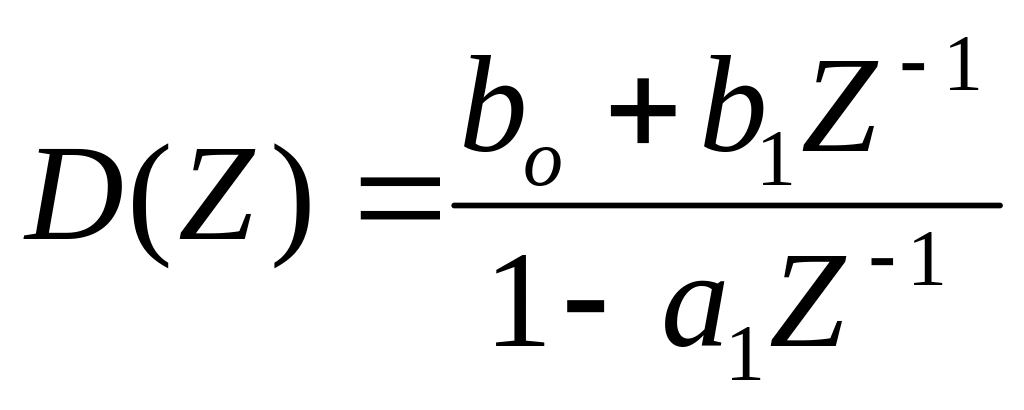(10.38)

Різницеве рівняння, яке описує цю функцію має вигляд:

(10.39)

Рівняння (10.39) відповідає неперервному коректуючому алгоритму:

(10.40)

Для малих значень періоду дискретизації Т, та при реалізації алгоритму диференціювання методом простої різниці диференційного рівняння (10.40) для такту [n] можна записати у вигляді різницевого рівняння:

або

(10.41)

Для малих значень періоду дискретизації Т, різницевого рівняння (10.39) ДПФ (10.38) збігається із коректуючим алгоритмом (10.42).

Якщо в (31) підставити , то отримаємо:

(10.42)

На підставі рівняння (33) знаходимо ДПФ окректуючого алгоритму:

(10.43)

Передавальна функція ланки диференціювання у цьому випадку має такий вигляд:

(10.44)

Розглянуті ДПФ коректуючих ланок дають змогу використавши методику аналізу неперервних систем автоматичного керування для ЦСАК знайти