10.3 Дискретна передавальна функція неперервної частини цсак
ЦСАК з КМЕОМ є дискретними системами, що характеризуються наявністю дискретизації керуючих сигналів за часом і рівнем. Дискретизація ЦСАК за рівнем робить їх нелінійними, а за часом – імпульсними.
Дискретизація сигналів за рівнем виконується АЦП (аналоговим цифровим перетворювачем). Дискретизація сигналів за часом у ЦСАК обмежується швидкістю КМЕОМ, яка виконує даний алгоритм керування.
При розгляді дискретної передавальної функції неперервної частини ЦСАК дискретизацією за рівнем можна знехтувати, так як в КГ (каналі керування) здебільшого використовуються багаторозрядні АЦП і ЦАП (цифро-аналогові перетворювачі).
С
труктурні
схеми ЦСАК та КМЕОМ можуть бути різними.
На рисунок 10.5 приведена спрощена
структурна схема ЦСАК.
Рисунок 10.5 – Структурна схема ЦСАК
На рисунок а приведено структурну схему ЦСАК в якій як завдання (t), так і керована величина (t) приведено в зображенням по Лапласу є неперервними величинами і в ЦСАК використовуються тоді коли датчики мають аналогові виходи. В такій ЦСАК неперервний сигнал похибки ((t)), перетворений по Лапласу ((p)), приходить до вхідного АЦХ з коефіцієнтом k, де – коефіцієнт підсилення. Опитування АЦП здійснюється в дискретні моменти часу (X(n)), по команді із КМЕОМ.
В ЦСАК структурна схема, якої на рисунок б, як завдання (n), так і керована величина (n) надходять до КМЕОМ до КМЕОМ від цифрових датчиків і є решітчастими функціями. Після цифрової обробки відповідно до коректуючого алгоритму сигнал похибки , у вигляді решітчастої функції через імпульсний елемент (ІЕ) надходить до ЦАП з коефіцієнтом передачі АЦП. Вихідний перетворювач одночасно з екстраполяторомнульового порядку (фіксуючим елементом) сигнал на виході якого на протязі періоду дискретизації Т залишається сталим. При визначенні дискретної передавальної функції неперервної частини ЦСАК повинні бути враховані коефіцієнти АЦП і ЦАП. Якщо одиниці молодших розрядів цих коефіцієнтів мають однакове значення, то добуток (1/АЦП)АЦП=1.
Це приводить до спрощення розрахунків, коли ми цей добуток приймаємо рівним 1. екстраполятор нульового порядку разом із неперервною частиною ЦСАК, тобто WH(p), формує передавальну функцію, яка визначається виразом.
(10.1)
А передавальна функція всієї розподіленої ЦСАК разом із КМЕОМ має вигляд:
(10.2)
–
дискретна
передавальна функція програмної
реалізації алгоритму керування ЦСАК
(дискретна передавальна функція КМЕОМ).
Дискретну передавальну функцію неперервної частини ЦСАК можна виразити через зведену неперервну функцію (рівняння (1)), а саме:
(10.3)
Якщо передавальна функція є добутком кількох більш простих передавальних функцій, тобто:
,
то
дискретна передавальна функція
не може бути визначена як добуток Z
перетворень, тому:
(10.4)
При
послідовному з’єднанні неперервних
ланок з передавальними функціями
результуюча дискретна передавальна
функція буде визначатися виразом:
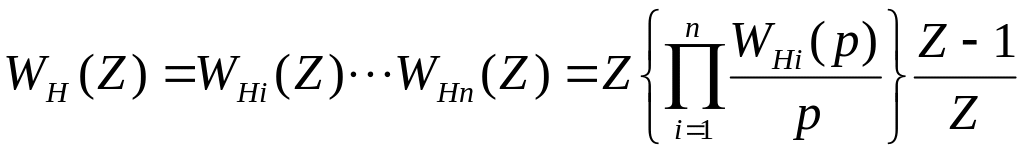(10.5)
Якщо між цими ланками є імпульсний елемент, то неперервна частина буде дорівнювати:
(10.6)
Дискретну передавальну функцію зведеної неперервної ЦСАК можна знайти за допомогою таблиці z–перетворень, або після розкладання цієї частини на прості дроби.
Нехай
ЦСАК має дискретну передавальну
і екстраполятор нульового порядку на
вході.
Передавальна функція її неперервної частини має має вигляд:
, (10.7)
де К – добротність за швидкістю неперервної частини ЦСАК;
То – постійна часу аперіодичної ланки першого порядку.
Нам необхідно визначати дискретну передавальну функцію неперервної частини системи.
Скориставшись таблицею z–перетворень передавальних функцій отримаємо.
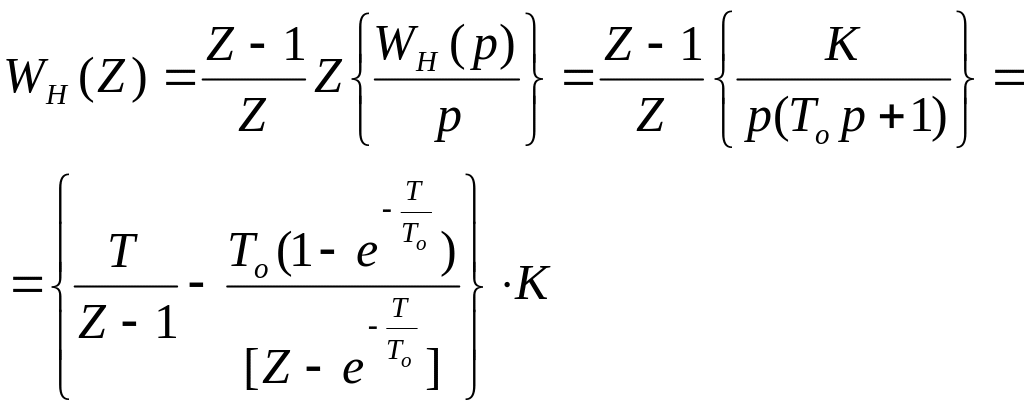(10.8)
Цю саму функцію можна визначити, якщо передавальну функцію розкласти на прості дроби, а потім для кожного окремого дробу знайти z–перетворення.
(10.9)