8 Нечітке моделювання багатовимірних нелінійних процесів

Нечітка логіка, як сучасний метод опрацювання сигналів, застосовується не тільки для керування, а також і для моделювання нелінійних процесів. Базуючись на базі даних знань, нечітка логіка дозволяє описувати основні зв’язки між змінними входу і виходу.

Перевагою нечіткої логіки в порівнянні з застосуванням нейронних мереж є низька кількість масивів даних, що є необхідним для відтворення нелінійного режиму процесу.

Але додатково до ступенів свободи потрібно знати:

• число нечітких множин;

• розподіл нечітких множин;

• функції приналежності;

• оператори.

Структура нечіткої моделі може бути змінена, так щоб відтворити режим вводу – виводу нелінійного процесу.

Розглянемо це на прикладі посудини під тиском із водопаровою сумішшю, яка характеризується комбінацією великої кількості параметрів, що мають вплив на стан процесу (тиск, рівень води, температура, вміст пари, масова витрата, тепловий потік). Термодинаміка і термодинамічні процеси у посудині під тиском із водопаровою сумішшю характеризуються нелінійністю, джерелами якої є:

• нелінійна структура моделі;

• коефіцієнти часової залежності у рівняннях моделі;

• нелінійний режим у результаті зміни стану процесу.

Глобальною задачею є визначення граничного рівня h_с у межах визначених зон посудини під тиском протягом градієнтів негативного тиску (dp/dt < 0), який відбувається в результаті відпливів.

Гібридний спостерігач був запропонований, щоб вирішити цю проблему регулювання технологічним процесом. Гібридний спостерігач комбінує класичний лінійний спостерігач із нечітко-заснованою адаптацією матриць моделі спостерігача (рівняння 8.1).

Класичний спостерігач базується на лінеаризованому спостерігачу, моделі рівняння (8.1), що описує залежність між перепадом тиску dp/dt і граничним рівнем h_c у ряді n зон посудини під тиском:

,

де і (8.1)

Елементи а₁₁…а_nn матриці системи А_b і елементи b₁₁…b_nn матриці входу В_b залежать від зміни параметрів процесу: тиску, перепаду тиску і так далі. Нечітко – заснований алгоритм для адаптації елементів матриць А_b і В_b допускає компенсацію нелінійності й удосконалення оцінки якості.

Структурний аналіз орієнтований на створення нечітких алгоритмів для обчислення елементів b₁₁…b_nn матриці входу В_b.

Елементи матриці входу В_d залежать від технологічних параметрів тиску (фактичний тиск p(t), початковий тиск P₀ на початку розгерметизації) і критичного рівня (початковий критичний рівень h_co на початку розгерметизації),

(8.2)

З мінні процесу:

u – вхідні змінні, q – змінні стану,

x – вихідні змінні, v – збурення,

z – метрологічні збурення.

Змінні спостерігача:

– змінні стану, – вихідні змінні,

e_x – похибки, K – матриця спостереження.

Рисунок 8.1 – Структура гібридного спостерігача

Нечіткі алгоритми застосовуються для відтворення залежності між вхідними змінними фактичного тиску p(t), початкового P_o, початкового критичного рівня h_co і вихідної змінної матричного елемента b (рисунок 8.2), який є необхідним для обчислення, заснованого на моделі спостерігача (8.1), критичного рівня.

Рисунок 8.2 – Нечітке моделювання вхідного матричного елемента b.

Для відтворення моделі вхід-вихід були представлені три варіанти структур нечітких моделей:

• комплексна структура моделі;

• паралельна структура моделі;

• каскадна структура моделі.

У першій структурі, визначеної як комплексна, використовувалась одна багатомірна нечітка модель. Друга структура, паралельна, характеризована застосуванням одновимірних нечітких моделей, розміщених паралельно. Третя структура, каскадна, містить два каскади двовимірних нечітких моделей.

Протягом створення нечіткої моделі треба вирішати декілька задач: фазіфікація, визначення бази знань і дефазіфікація (рисунок 8.3). За допомогою операції фазіфікації визначають число невизначених множин і форми приналежності. У процесі фазифікації використовують трикутну функціональну залежність.

Рисунок 8.3 – Компоненти нечіткої моделі.

Нечітка модель може бути створена на база моделі Mamdani - типу та на базі моделі Sugeno - типу. У моделі Mamdani - типу моделюють чіткий вихідний сигнал, який був отриманий після процесу дефізіфікації. У цьому випадку число наборів, форми залежності функції і методи дефазіфікації повинні бути визначені.

У моделі Sugeno з’являється проблема визначення лінійної вихідної функції. Для тривимірного об’єкта вихідна функція може бути описана наступним рівнянням:

f_i{p(t), P₀, h_co} = k_1i p(t) + k_2i P₀ + k_3i h_co, (8.3)

де k_ij змінні впливу сигналів;

i – номер вихідної функції Sugeno;

j – номер вихідного сигналу.

Усі змінні повинні бути визначені у моделі, що регулює процес.

Перевірка адекватності визначених нечітких моделей базується на критерії:

, (8.4)

де b_R – матриця елементів контрольної точки;

b_FM – матриця елементів нечіткої моделі.

Нечітка модель, заснована на багатовимірювальному нечіткому алгоритмі із вхідними змінними фактичного тиску p(t), початкового тиску P_o, початкового критичного рівня h_co і вихідної змінної матричного елемента b(t) зображена на рисунку 8.4.

Рисунок 8.4 – Визначення матричного елемента b(t) за допомогою нечіткої моделі.

Ці три вхідні сигнали були фазіфіковані на різну кількість нечітких множин (рисунок 8.5).

Лінгвістична змінна початкового тиску P₀ була подана двома нечіткими множинами “низько” і “високо”.

Лінгвістична змінна початкового критичного рівня h_co була описана з використанням трьох множин “низько”, “нормально” і “високо”.

Д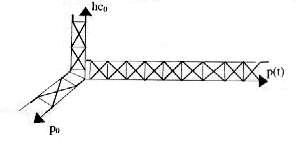 ля фазіфікації використовувалися тиски p(t) 14 нечітких множин і асиметрична фазіфікація (рисунок 8.5).

Рисунок 8.5 – Фазіфікація вхідних сигналів.

У моделі Mamdani – типу достатня якість була досягнута використанням 29 звужених трикутних вихідних нечітких множин (рисунок 8.6)

Рисунок 8.6 – Вихідні нечіткі множини.

Р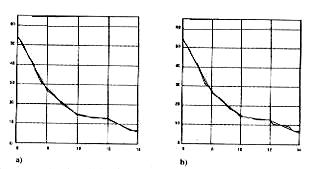 исунок 8.7 – Відповідна комплексна нечітка модель: а) для h = 1; b) для h = 0,5.

Розширена постійна функціональна залежність є важливим параметром для точного нечіткого моделювання. На рис. 8.7 а, і 8.7 b, показані криві відповідної комплексної нечіткої моделі для двох різних видів потрійної нечіткої множини. Був отриманий кращий результат для розширеного h = 1. Краща якість моделювання для моделі Mamdani була отримана асиметричною фазіфікацією лінгвістичної змінної фактичного т иску (рисунок 8.8).

Рисунок 8.8 – Асиметрична фазіфікація тиску.

Р исунок 8.9 – Mamdani (а) і Sugeno (b) моделюють поверхню для Р₀ = 14 бар.

Створені на фазі-основі поверхні показані на рисунку 8.9 (а) для моделі Mamdani - типу і для моделі Sugeno - типу на рисунку 8.9 (b).

Точність наближення е_sq для моделі Mamdani - типу змінюється в межах 1,16-3,05, для моделі Sugeno - типу 25,07-91,58.

Отже, моделі Mamdani - типу характеризується кращою точність оцінки помилок змінних е_sq. Ця точність була досягнута високим числом нечітких множин для вихідної змінної. Для проектування Sugeno – типу моделі було використано дев’ять трьохвимірних функцій.

Конструкція обох моделей була характеризована високою кількістю правил.

Визначення матричного елемента b(t) було реалізовано паралельними структурами 1D - контролерів.

Паралельна структура (рисунок 8.10) вміщує в себе:

• фазі-контролери з нечітким алгоритмом;

• спеціальні нечіткі моделі, що обчислюють значення членства для початкового тиску Р₀ (нечіткі множини “низько” і “високо”) і для початкового критичного рівня h_co (нечіткі множини “низько”, “нормально” і “високо”).

• д одатковий алгоритм, щоб визначати кінцеве значення для матричного елемента b(t).

Рисунок 8.10 – Визначення матричного елемента b(t) за допомогою паралельної структури ID – регулятора з нечітким алгоритмом.

Рисунок 8.11 представляє поверхні простих нечітких моделей, призначених для початкового значення тиску Р₀ = 14 бар і різних значень початкового критичного рівня h_co = 105 см, h _со = 155 см і h_со = 195 см.

Рисунок 8.11 – Поверхня трьох простих нечітких моделей, призначених для Р₀ = 14 бар і різних початкових критичних умов рівнів h_co = 105 см, h_со = 155 см і h_со = 195 см.

Показана на рисунку 8.9 (комплексна модель) ілюструє розбивку поверхні на три окремі поверхні, що визначені для спеціальних значень початкових критичних рівнів.

Рисунок 8.12 показує наявність поверхні для простої нечіткої моделі (Р₀ = 14 бар, h_co = 105 см) з симетричною і несиметричною фазіфікацією лінгвістичних змінних тиску p(t).

Рисунок 8.12 – Поверхня для простої моделі із симетричною (а) і асиметричною (b) фазіфікацією.

Точність наближення е_sq для описаних простих моделей перерахована в таблиці 8.1. Щоб одержати гарну точність і гладку поверхню, потрібно використовувати асиметричну фазіфікацію і велику кількість (у максимумі 14) наборів для лінгвістичної змінної p(t).

Таблиця 8.1 – Порівняння помилки е_sq для прикладів нечітких моделей і для контрольних точок.

Прості Mamdani–типу моделі
BD14H105	BD14H155	BD14H195	BD22H105	BD22H155	BD22H195
3.31	1.54	2.93	3.81	2.53	4.14
7 симетричних множин і симетрична фазіфікація Операції І (мінімум), значення (мінімум)
33.88	21.25	19.31	30.10	21.55	27.19
7 симетричних множин і симетрична фазіфікація Операції І (мінімум), значення (мінімум)
20.76	10.87	9.87	18.58	12.13	15.98
7 симетричних множин і симетрична фазіфікація Операції І (мінімум), значення (мінімум)
3.12	1.35	2.26	4.04	2.65	3.85
7 симетричних множин і симетрична фазіфікація Операції І (мінімум), значення (мінімум)
2.61	1.08	1.94	3.57	2.43	2.88

Прості Mamdani–типу моделі
BD14H105	BD14H155	BD14H195	BD22H105	BD22H155	BD22H195
23.99	13.03	13.26	23.08	11.93	35.86

У результаті порівняння точності між моделлю Mamdani і Sugeno (див. таблицю 8.1), моделі Mamdani було віддано перевагу.

Перевагою паралельної структури простих моделей є низьке число правил у кожній простій моделі.

Детеміновані матричні елементи b(t) можуть бути реалізовані каскадною структурою нечітких моделей, що розроблені для низького і високого значення початкового тиску (рисунок 8.13):

• нечітка модель із змінною входу фактичного тиску p(t) і зміною вихідного сигналу b*(t);

• нечітка модель із вхідними змінними b*(t), початковим критичним рівнем h_со і вхідним змінним матричним елементом b(t);

• алгоритм для визначення вихідного сигналу кожного каскаду, заснованого на початковому тиску Р₀.

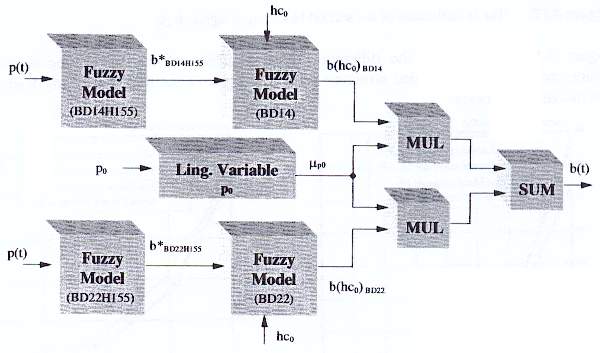
Рисунок 8.13 – Визначення матричного елемента b(t) за допомогою каскадної структури нечітких моделей.

Перші блоки каскадів подібні простим моделям контрольних точок BD14H155 i BD22H155. Процес фазіфікації першим блоком вхідного сигналу p(t) подібний до складних нечітких моделей (рисунок 8.8).

Дугий блок кожного каскаду є двохмірною моделлю, і слугує для приймання вихідного сигналу першого блока. Напрямок руху залежить від наступного (другого) входу змінної h_co. Одержувана гладка поверхня в межах наступного блока ділиться на ділянки необхідні для вхідних нечітких множин. Фазіфікація наступного (другого) блока вхідного сигналу b*(t) є більше ускладненою, така нечітка множина демонструється на рисунку 8.14.

Рисунок 8.14 – Фазіфікація наступного (другого)блока вхідного сигналу b(t).

Точність наближення е_sq для розробленої моделі, перерахована в таблиці 8.2.

Таблиця 8.2 – Порівняння помилки е_sq для визначення нечітких моделей і контрольних точок.

Паралельна каскадна Mamdani–типу модель
BD14H105	BD14H155	BD14H195	BD22H105	BD22H155	BD22H195
3.31	1.54	2.93	3.81	2.53	4.14

Для всіх трьох структур нечіткого моделювання була доведена спроможність інтерполяції у випадку невідомих значень вхідних змінних, що не є контрольними точками. Усі досліджувані структури ведуть до гарних результатів для невідомих параметрів.

Базуючись на значеннях помилки з цих шести контрольних точок середня помилка для трьох структур була розрахована і подана в таблиці 8.3. Можна зробити висновок, що середньою помилкою буде майже та ж саме значення для всіх структур. Каскадна структура веде до більш високих значень помилок.

Структура каскадної моделі більше ускладнена ніж інші.

Прості блоки паралельної структури можуть бути розроблені дуже просто і можуть бути дубльовані для контрольних точок на підключенні з модифікацією і адаптацією до спеціальних умов.

Таблиця 8.3 – Порівняння середньої е_sq для нечітких модельних структур.

Показники	Структура нечіткої моделі
	Комплексна	Паралельна	Каскадна
Число вхідних нечітких множин	19	10 для кожної простої моделі + 5	9+2/14+2 перший блок 35 – другий блок
Число вхідних змінних	29	8…12	30 – перший блок 40 – другий блок
Число правил	69	8…12	9/14 – перший блок 93 – другий блок
Середня помилка апроксимації	2,21	2,42	3,04

Для розглянутого об’єкту є краща паралельна структура, яка дозволяє спрощену оптимізацію і досить просте розширення.

Отже можемо зроби такі висновки:

1. Нечіткі множини можуть бути використані з успіхом для моделювання нелінійних характеристик;

2. Для описаного прикладу процесу за допомогою методу Sugeno досягається добра точність моделювання;

3. Симетричний або несиметричний метод фазіфікації має великий влив на точність моделювання;

4. Комплексні нечіткі моделі забезпечують достатньо точне моделювання, але це потребує багато правил і вихідних нечітких множин;

5. Кращі результати моделювання отримано використанням декількох однорозмірних нечітких моделей у паралельному циклі;

6. Паралельна каскадна схема є компромісом між точністю моделювання і складністю нечіткої моделі.