6.7. Регулятори безперервної дії

Автоматичний регулятор поєднує в собі вимірювальний, регулюючий і виконуючий пристрої. При самому агрегатному принципі побудови сучасного регулятора ці три його основних блоки конструктивно виконуються роздільно. Оскільки закон регулювання формується регулюючим пристроєм, воно вважається основним блоком. Тому часто під терміном «регулятор» розуміють «регулюючий пристрій». В цьому випадку при розрахунку систем автоматичного регулювання необхідно окрім об'єкту і «регулятора» (регулюючого пристрою) враховувати як самостійні елементи вимірювального і виконавчого пристроїв.

Відомо дві форми запису закону регулювання. Відповідно до моделей регуляторів, представлених в попередніх розділах, поточне значення х_т регульованого параметра повинне подаватися на вхід регулятора із зворотним знаком. При цьому на виході регулятора формується регулююче дію

у =f(ε), де ε =х_з-х_т . (6.63)

Проте в реальних конструкціях регуляторів часто вихідна величина об'єкту подається на вхід регулятора з тим же знаком. Тоді регулююче дію повинне підкорятися співвідношенню

у =–f(ε’), де ε =х_т-х_з (6.64)

тобто при використовуванні ε’ =х_т-х_з необхідно так сформувати регулюючу дію у, щоб воно компенсувало розузгодження.

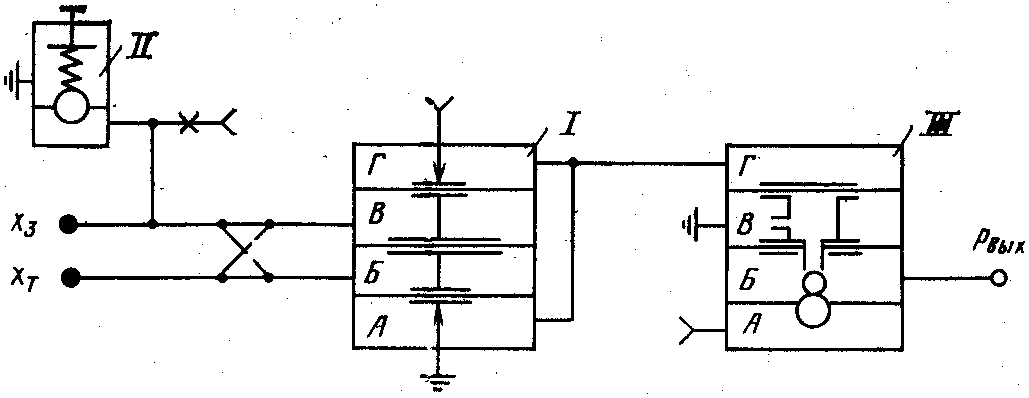
Рисунок 6.37 – Позиційне регулююче пристрій ПР1.5

Зберігши заводську форму запису і позначивши вихідну величину регулюючого пристрою х_вих, матимемо у вигляді, що регулююча дія у по співвідношенню (6.64) повинна забезпечуватися відповідним включенням виконавчого і вимірювального пристроїв.

Позиційне (Пз) регулююче пристрій ПР1.5 (рис. 6.37) складається з елементу порівняння І, задаючого пристрою ІІ і підсилювача потужності ІІІ. При виході регульованого параметра за встановлене значення пристрій видає дискретні пневматичні сигнали «О» або «1» відповідно до рівнянь

х _вих =1 при х_т –х_з >0; при настройці

х_вих =0 при х_т –х_з <0; на максимум; (6.65)

х _вих =1 при х_т –х_з >0; при настройці

х_вих =0 при х_т –х_з <0; на мінімум. (6.66)

Регулюючий пристрій настроюється на максимум або мінімум перемиканням вхідних каналів. Розглянемо роботу пристрою, наприклад, при його настройці на мінімум (включення вхідних каналів по суцільних лініях на рис. 6.37). Сигнал, пропорційний поточному значенню х_т регульованого параметра, поступає в камеру В, а завдання х₃ – в камеру Б елементу порівняння І. Поки поточне значення більше заданого, збірка мембран знаходиться у верхньому положенні, сопло живлення закрито, а вихідна лінія сполучена через камеру А і нижнє сопло з атмосферою. Сигнал на виході рівний 0. Як тільки поточне значення стане менше завдання, збірка мембран перейде в нижнє положення, відкриваючи сопло живлення і закриваючи вихід в атмосферу. На виході елементу порівняння буде сигнал х_вих=1. Цей сигнал поступає на вхід повторювача підсилювача потужності ІІІ.

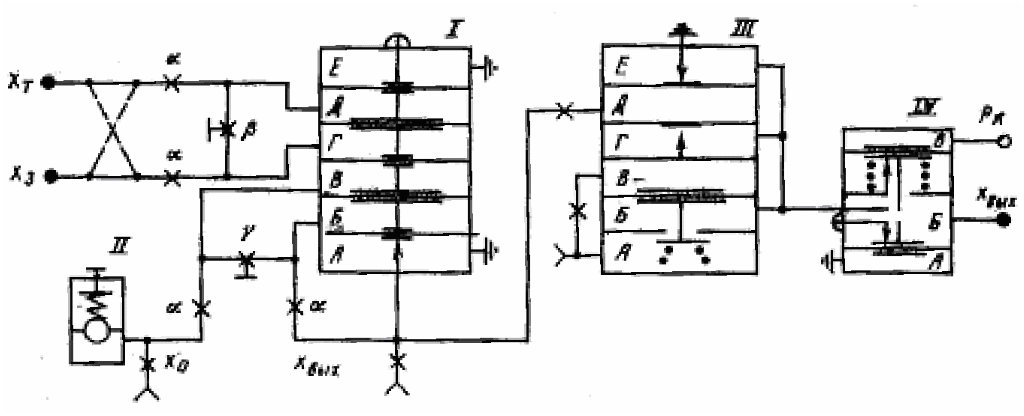Рисунок 6.38 – Пропорційне регулюючий пристрій з лінійними статичними характеристиками ПР2.8

Блок ІІІ знаходиться в рівновазі, коли тиск в камері Б рівно тиску в камері Г. При збільшенні тиску в камері Г збірка мембран відсовує подвійний кульковий клапан, пропускаючи повітря живлення з камери А в камеру Б і на вихід. Завдяки значному прохідному перетину кулькового клапана вихідний сигнал посилюється по потужності (витраті).

Пропорційне (П) регулюючий пристрій з лінійними статичними характеристиками ПР2.8 (рис. 6.38) складається з двохсоплового підсилювача (п'ятимембранного елементу порівняння) І, задаючого пристрою ІІ, підсилювача потужності ІІІ і вимикаючого реле IV. Сигнал x_т, пропорційний поточному значенню регульованого параметра, поступає в камеру Д підсилювача-суматора І, а сигнал х₃, пропорційний заданому значенню, – вкамеру Г. Зусилля, створювані цими сигналами, діють на мембрани елементу порівняння і врівноважуються силами, діями вихідного сигналу в лінії зворотного зв'язку х_вих і опорного сигналу х₀, що розвиваються. Ступінь дії зворотного зв'язку визначається настройкою регульованих опорів. Лінійність статичних характеристик досягається введенням двох суматорів в прямий канал і в лінію зворотного зв'язку. Позначимо постійні опори в обох суматорах α, а зміні – β і γ (див. рис. 6.38).

Розглянемо випадок, коли γ =О. Умова рівноваги елементу порівняння матиме вигляд

р_д –р_г +х₀ –х_вих =0 (6.67)

або

х_вих = р_д –р_г +х_0. (6.68)

Використовуючи рівняння (6.36) для суматора на опорах, можна записати

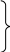
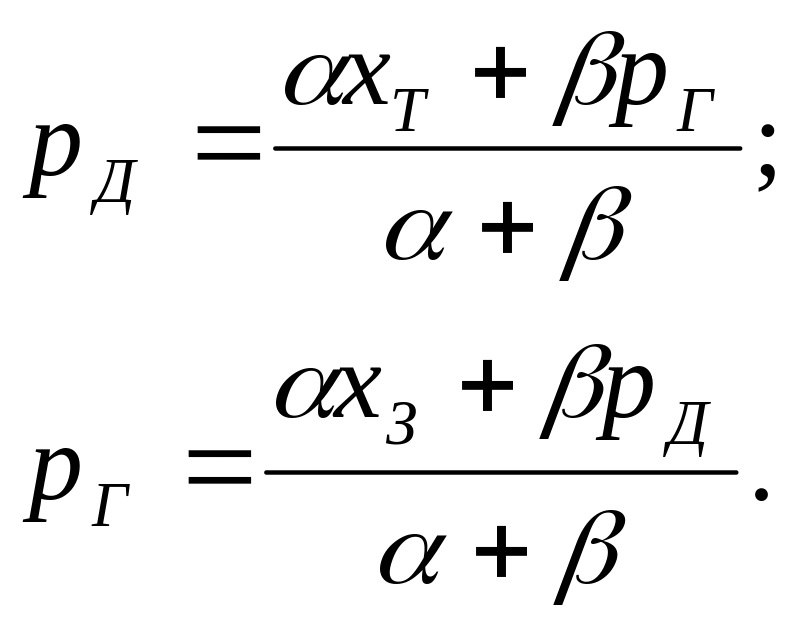(6.69)