6.2 Математичні моделі і способи реалізації автоматичних регуляторів

Залежність зміни вихідної величини регулятора у від розузгодження  заданого х₃ і поточного х_т значень регулюючого параметра х є законом регулювання. Основними показниками якості загальнопромислових автоматичних регуляторів слід вважати динамічну точність і надійність реалізації заданого закону регулювання. Очевидно, що сконструювати регулятор, що абсолютно точно реалізовує заданий закон регулювання, практично неможливо. Тому регулятори, які точно відтворюють рівняння, що приводяться далі, називаються ідеальними. Реальні конструкції регуляторів описуються рівнянням, які в меншому або більшому ступені відрізняються від ідеальних, що приводить до деякої зміни якості регулювання в порівнянні з розрахунками.

а — закон регулювання; б — графік перехідного процесу в системі з Пз-регулятором; в — структурна схема

Рисунок 6.6 – Характеристики Пз-регулятора:

Позиційними (Пз) називають регулятори, у яких вихідна величина приймає одне з своїх дискретних значень y_max або y_min залежно від знаку розузгодження :

(6.5)

Закон регулювання показаний на рис. 6.6, а. В реальних умовах характеристика регулятора істотно відрізняється від ідеального (пунктир на рис. 6.6, а), утворюючи, зокрема, зону нечутливості а. Поява зони а приводить до збільшення запізнювання  контура регулювання. Тому в цілях розширення області застосування позиційних регуляторів і поліпшення перехідних процесів величину а бажано мати по можливості мінімальною. Проте в практиці автоматичного регулювання зустрічаються задачі, де зона нечутливості позиційного регулятора повинна бути достатньо великою, наприклад при регулюванні рівня у великих ємностях. Виходячи з цього в позиційних регуляторах бажано мати пристрої, що дозволяють настроювати величину а в широких межах.

Типовий графік перехідного процесу в системі з позиційним регулятором при стрибкоподібній зміні збурення z показаний на рис. 6.6, б (крива 2). Тут же приведений вид перехідного процесу в статичному об'єкті регулювання без регулятора (крива 1). Очевидно, вживання позиційного регулятора можливе при допустимості автоколивального процесу в системі і при певних значеннях амплітуди сталих коливань.

Пропорційними (П) називають регулятори, у яких вихідна величина пропорційна величині розузгодження:

(6.6)

Коефіцієнт пропорційності К в цьому виразі називається коефіцієнтом підсилення регулятора і є його настроювальним параметром.

Передавальна функція П-регулятора

(6.7)

Закон регулювання при стрибкоподібному відхиленні поточного значення регулюючого параметра від заданого показаний на рис. 6.7, а. З виразу (6.6) виходить, що кожному значенню розузгодження  відповідає цілком певне значення вихідної величини регулятора, тобто П-регулятор, а отже, і система в цілому можуть знаходитися в стані рівноваги при різних значеннях регулюючого параметра. Таким чином, П-регулятор не усуває розузгодження, він лише приводить систему до нового стану рівноваги, відповідного нового значення регулюючого параметра.

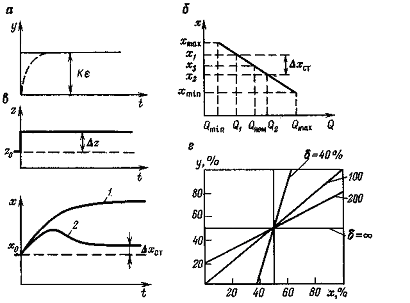
а — закон регулювання; б — статична характеристика системи з П-регулятором; в— графік перехідного процесу в системі з П-регулятором; г—статичні характеристики П-регулятора

Рисунок 6.7 – Характеристики П-регулятора:

Величина залишкового відхилення регулюючого параметра називається статичною нерівномірністю або статичною помилкою П-регулятора.

Явище статичної нерівномірності добре ілюструється статичною характеристикою системи з П-регулятором (рис. 6.7, б), що є залежністю значень регулюючого параметра х від навантаження об'єкту Q.

Припустимо, що система знаходиться в стані рівноваги при навантаженні Q₁ і значенні регулюючого параметра х₁. При зміні навантаження до величини Q₂ регулюючий параметр х зміниться, П-регулятор створить регулюючу дію відповідно до виразу (6.6) і приведе регулюючий параметр до значення х₂. Таким чином, статична нерівномірність

(6.8)

залежить від навантаження і коефіцієнта підсилення регулятора К. Чим більше коефіцієнт підсилення регулятора, тим більша величина регулюючої дії і тим менше залишкове відхилення регулюючого параметра. З цієї точки зору доцільно збільшувати коефіцієнт підсилення П-регулятора. Проте, оскільки зміна регулюючої дії відображається на регулюючому параметрі не миттєво, а після закінчення деякого часу, яке визначається властивостями об'єкта регулювання, слід обмежувати коефіцієнт підсилення регулятора К з метою запобігання надмірного регулювання. Тому величину коефіцієнта підсилення регулятора визначають розрахунковим шляхом для кожної конкретної системи.

Типовий графік перехідного процесу в системі з П-регулятором при стрибкоподібній зміні збурення z показаний на рис. 6.7, б (крива 2). Тут же приведений вид перехідного процесу в статичному об'єкті регулювання без регулятора (крива 1). Перевага П-регулятора полягає в швидкому відновленні рівноваги в системі, а наявність статичної нерівномірності є недоліком П-регулятора.

Настроювальним параметром П-регулятора є його коефіцієнт підсилення К.

Разом з тим на практиці як параметр настройки П-регулятора використовується величина, зворотна коефіцієнту підсилення К, виражена у відсотках:

(6.9)

Величина  називається межею пропорційності регулятора. Вона визначає інтервал зміни регулюючого параметра (вираженого у відсотках), що викликає зміни вихідної величини регулятора від одного крайнього значення до іншого (рис. 6.7, г). Настройка межі пропорційності на значення більше 100 % означає, що вихідна величина регулятора не досягає своїх крайніх значень при зміні регулюючого параметра у всьому діапазоні. Згідно рівнянню (6.6) при рівності поточного і заданого значень регулюючого параметра (=х_з–х_Т=0) вихідна величина регулятора рівна нулю, тобто регулюючий орган виконавчого пристрою повинен займати одне з своїх крайніх положень.

Рисунок 6.8 – Структурні схеми реалізації П-регуляторів

Щоб при х_Т = х₃ регулюючий орган міг займати проміжне положення в межах свого ходу, в реальних конструкціях регуляторів передбачається введення додаткової складової на виході регулятора у₀, причому так, щоб при х_Т = х₃ дотримувалося умова у=у₀

Тоді рівняння П-регулятора має вигляд

(6.10)

Крім того, в реальних регуляторах зважаючи на їх деяку інерційність закон регулювання дещо відрізняється від ідеального (рис. 6.7, а, пунктир).

Рівняння (6.10) може бути реалізовано структурою, що показана на рис. 6.8, а. Для підвищення динамічної точності П-регулятора його часто реалізують у вигляді підсилювача з більшим коефіцієнтом підсилення, охопленого від’ємним зворотнім зв'язком, як це показано на рис. 6.8, б. Тоді в відповідностю з цією структурою передавальна функція регулятора визначиться з виразу

(6.11)

При K_у

(6.12)

Інтегральними (І) називають регулятори, у яких вихідна величина пропорційна інтегралу від розузгодження:

(6.13)

де Т_І — постійна часу інтеграції, є настроювальним параметром І-регулятора.

Передавальна функція І-регулятора

(6.14)

Закон регулювання при стрибкоподібному відхиленні поточного значення регулюючого параметра від заданого показаний на рис. 6.9, а.

Вираз (6.13) в диференціальній формі має вигляд

(6.15)

Звідси видно, що відхилення регулюючого параметра  пропорційне не значенню вихідної величини, а її швидкості. Отже, в стані рівноваги при dy/dt=0, розузгодження  також рівне нулю. Таким чином, при всякому відхиленні регулюючого параметра від заданого вихідна величина І-регулятора змінюватиметься до тих пір, поки це відхилення не буде рівне нулю. Це можливо при будь-кому значеню збурення (навантаження). Статична характеристика системи з І-регулятором, приведена на рис. 6.9, б, показує, що система може знаходитися тільки в одному стані рівноваги — коли поточне значення регулюючого параметра рівне заданому. Іншими словами, І-регулятор здійснює регулювання без статичної помилки (х_ст=0).

а —закон регулювання; б — статична характеристика системи з І-регулятором; в — графік перехідного процесу в системі з І-регулятором; г — структурна схема

Рисунок 6.9 – Характеристики І-регулятора:

Типовий графік перехідного процесу в системі з І-регулятором при стрибкоподібній зміні збурення z показаний на рис. 6.9, в. Тут же приведений вид перехідного процесу в статичному об'єкті регулювання без регулятора (крива 1).

Перевагою І-регулятора в порівнянні з П-регулятором є відсутність статичної нерівномірності.

Недоліки І-регулятора обумовлені їх динамічними властивостями. Як би малим не було розузгодження , І-регулятор буде продовжуватиме переміщати регулюючий орган аж до крайнього положення. Напрям руху регулюючого органу змінюється лише у тому випадку, коли поточне значення регулюючого параметра, змінюючись, переходить через задане значення.

Рисунок 6.10 – Закон регулювання ПІ-регулятора

І-регулятори можуть стійко працювати тільки на об'єктах з великим самовирівнюванням і малим запізнюванням. Тому І-регулятори як самостійні пристрої застосовуються вкрай рідко. Вони можуть бути реалізовані відповідно до структури, показаної на рис. 6.9, г, тобто у вигляді інерційної ланки, охопленої позитивним зворотним зв'язком. Проте найбільш часто І-регулятори конструктивно об'єднуються з П-регулятором.

Пропорційно-інтегральними (ПІ) називаються регулятори, у яких вихідна величина пропорційна відхиленню регулюючого параметра і інтегралу від цього відхилення:

(6.16)

У такому регуляторі коефіцієнт підсилення К і постійна часу інтеграції Т_І є його настроювальними параметрами.

Передавальна функція ПІ-регулятора має вигляд

(6.17)

Закон регулювання при стрибкоподібному відхиленні поточного значення регулюючого параметра від заданого показаний на рис. 6.10. Вираз (6.16) в диференціальній формі має вигляд

(6.18)

тобто швидкість зміни регулюючої дії пропорційна розузгодженню і його швидкості. Отже, в стані рівноваги при dy/dt=0 і d/dt = 0 розузгодження  також рівне нулю.

З виразу (6.16) виходить, що в ПІ-регуляторі поєднуються кращі властивості П- і І-регуляторів. При стрибкоподібному відхиленні поточного значення від заданого ПІ-регулятор спочатку під дією пропорційної складової швидко приводить систему до нового стану рівноваги, відповідному цьому відхиленню, а потім під дією інтегральної складової ліквідовує це відхилення.

Рисунок 6.11 – Структурні схеми реалізації ПІ-регулятора

Таким чином, пропорційна складова забезпечує необхідні динамічні властивості системи, а інтегральна — статичні властивості, усуває статичну нерівномірність. Постійна часу інтеграції Т_і, що визначає зміну вихідної величини регулятора під дією інтегральної складової, називається також часом інтегрування або часом подвоєння, оскільки вона чисельно рівна часу, протягом якого зміна вихідної величини під дією пропорційної складової К подвоюється під дією інтегральної складової (рис. 6.10). Рівняння (6.16) може бути реалізоване структурою, показаною на рис. 6.11, а. Проте сучасні ПІ-регулятори зазвичай виконуються з використанням зворотних зв'язків (рис. 6.11, б). Тут зворотний зв'язок виконаний у вигляді реальної диференціюючої ланки з постійною часу, рівної постійній часу регулятора Т_і, і з коефіцієнтом підсилення, рівним зворотному коефіцієнту підсилення регулятора. Відповідно до цієї структури передавальна функція регулятора визначиться з виразу

(6.19)

При K_у

(6.20)

Реальна диференціююча ланка реалізується поєднанням жорсткого від’ємного і інерційного додатнього зворотніх зв'язків. Такий зворотний зв'язок в цілому називається пружним або ізодромним. Тому ПІ-регулятори часто називають ізодромними, а їх параметр налаштування Т_і — часом ізодрому: На рис. 6.10 пунктиром показаний закон регулювання реального ПІ-регулятора.

Рисунок 6.12 – Характеристики ПД-регулятора: а — закон регулювання; б — структурна схема

Пропорційно-диференціальними (ПД) називають регулятори, у яких вихідна величина пропорційна розузгодженню  і швидкості цього розузгодження

(6.21)

Коефіцієнт підсилення К і постійна часу диференціювання Т_д є параметрами настройки ПІ-регулятора.

Передавальна функція ПД-регулятора має вигляд

(6.22)

При стрибкоподібному відхиленні регулюючого параметра вихідна величина ПД-регулятора під дією диференціальної складової повинна миттєво зрости до нескінченно великої величини і також миттєво зменшитися до значення, що визначається пропорційною складовою (рис. 6.12). Проте, оскільки в реальних регуляторах неможливі миттєві процеси, практично закон регулювання має вигляд, показаний на рис. 6.12, а пунктиром.

Поєднання в ПД-регуляторі пропорційної дії і дії по похідній робить його менш інерційним в порівнянні з П-регулятором. Пояснюється це тим, що в момент виникнення розузгодження швидкість розузгодження виявляється швидше, ніж саме розузгодження.

Використовування в ПД-регуляторі дії по похідній (швидкості) відхилення означає введення в закон регулювання передуючої дії, тому ПД-регулятори називають пропорційними регуляторами з передуванням, а величину Т_Д — часом передування. Випередження вихідного сигналу в ПД-регуляторі в порівнянні з П-регулятором має істотно позитивне значення при регулюванні параметрів в об'єктах, що володіють великим запізнюванням. Недоліком ПД-регулятора є наявність, як і в П-регуляторі, статичної нерівномірності.

ПД-регулятор звичайно реалізують по схемі, показаній на рис. 6.12, б. Вона складається з двох блоків, сполучених послідовно — пропорційний з передавальною функцією

а — закон регулювання; б — структурна схема

Рисунок 6.13 – Характеристики ПІД-регулятора:

W_П(p) і диференціальний (блок передування) з передавальною функцією W_Д(p), причому останній представлений підсилюючою ланкою з великим коефіцієнтом підсилення Ку, охоплений інерційним від’ємним зворотним зв'язком.

Передавальна функція регулятора визначається з виразу

(6.23)

При Ку

(6.24)

Пропорційно-інтегрально-диференціальними (ПІД) називають, регулятори, у яких вихідна величина пропорційна розузгодженню , інтегралу і швидкості цього розузгодження:

(6.25)

Параметрами побудови регулятора є коефіцієнт підсилення К, час інтеграції Т_і і час передування Т_д.

Передавальна функція ПІД-регулятора має вигляд

(6.26)

Закон регулювання при стрибкоподібному відхиленні регулюючого параметра показаний на рис. 6.13, а. Пунктиром показаний закон регулювання реального ПІД-регулятора.

ПІД-регулятори володіють істотними перевагами в порівнянні зі всіма раніше розглянутими регуляторами відносно статичних і динамічних властивостей. Проте, будучи найскладнішими по конструкції, вони застосовуються лише при регулюванні найбільш істотних технологічних параметрів.

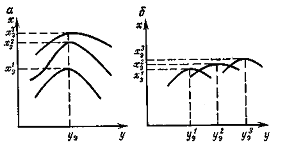
Рисунок 6.14 – Екстремальні статичні характеристики об'єктів

ПІД-регулятори можуть бути реалізовані по структурі, показаній на рис. 6.13, б.

Відповідно до цієї схеми передавальна функція ПІД-регулятора

(6.27)

З допомогоюю ПІД-регулятора можна здійснити, будь-який лінійний закон регулювання.

При Т_Д=0 і нескінченно великій величині Т_і одержимо П-регулятор. При Т_Д=0, встановивши достатньо малі значення К і Т_А, але так, щоб відношення К/Т_і було істотним, отримаємо І-регулятор.

При Т_Д=0 і кінцевих значеннях К і Т_і матимемо ПІ-регулятор, а при нескінченно великому значенні Т_і і кінцевих значеннях К і Т_Д—ПД-регулятор.

Екстремальними називають регулятори, які визначають і підтримують режим роботи об'єкту регулювання, відповідних екстремуму функції, що характеризує цей ре жим. Необхідною умовою екстремального регулювання є наявність екстремуму статичної характеристики об'єкту, яка залежно від зовнішніх умов може зміщуватися (рис. 6.14). Причому якщо екстремум х_е змінюється тільки по величині при незмінному значенні вхідної регулюючої дії у_е (рис. 6.14, а), то достатньо один раз визначити положення екстремуму, а потім використати звичайну систему автоматичного регулювання (стабілізації). В другому випадку (рис. 6.14,6) доцільно застосувати екстремальний регулятор, який разом з об'єктом утворює систему екстремального регулювання. Екстремальні системи відносяться до пошукових систем регулювання, в яких операція пошуку використовується для отримання додаткової інформації про об'єкт і визначення екстремуму. Процес пошуку здійснюється пробними регулюючими діями. Якщо пробна дія у на об'єкт викликає наближення регульованої величини х до екстремуму, то дія повторюється в тому ж напрямі. якщо пробна дія віддаляє регульовану величину від екстремуму, то напрям дії змінюється на зворотній.

Рисунок 6.15 – Показники якості системи екстремального регулювання

Рисунок 6.16 – Принципова схема регулятора температури прямої дії типу РТПД

Визначивши, що регульована величина досягла екстремуму, регулятор увійде до коливальний режим поблизу екстремального значення. При зсуві екстремальної характеристики операції пошуку екстремуму повторюються.

Характер коливань регулюючого параметра біля екстремуму в системі з екстремальним регулятором показаний на рис. 6.15. Якість регулювання такої системи визначається наступними показниками: зоною пошуку на виході х (рис. 6.15), періодом автоколивань Т, втратою на пошук Р, визначуваної як різниця між екстремальним х_е і середнім значеннями за період, часом виходу в екстремум (при стрибкоподібному його зсуві) .