5.2 Узагальнена умова Гурвіца

Розглянемо замкнену систему керування, описану наступними відношеннями:

(5.5)

де x означає стан вектора,

u - скаляр установки як входу так і виходу регулятора,

y - скалярна лінійна функція стану змінних.

Сигнал y безпосередньо не спостерігається в системі керування і може розглядатися як штучно впроваджений вихід. Крім того A₀, B₀ і H означають дійсні матриці: Нелінійна система (5.5) складається з “лінійної частини” і “нелінійної частини”. Передавальна функція лінійної частини “від u до y” рівна

Остання нерівність в системі (5.5) характеризує нелінійну частину, тобто функція u(t)=f[x(t)]

задовільняє сектор умов з додатніми константами L і K. Іншими словами, f належить сектору [L, K].

Визначення 1. Система (5.5) задовольняє узагальненій умові Гурвіца (або УУГ скорочено), якщо

(5.6)

де λ[A] означає будь-яке власне значення матриці А.

Відомо, що

• Будь-яка лінійна функція u(t)=ry(t) задовільняє сектор умов в (5.5), якщо і тільки якщо

• Навіть якщо (5.6) отримані, це не гарантує, що система (5.5) буде стійкою для кожної нелінійності f(x), що задовільняє сектор умов в (5.5).

• Незважаючи на те, що перевірка (5.6) є значно простішою ніж аналіз стійкості (5.5), виконання

УУГ даної в (5.6) є недостатньою для стійкості (5.5). Це є суть припущення Айзермана.

• Матриця A₀ може бути або може і не бути асимптотично стійкою. Якщо ні, то ми припускаємо, що система еквівалентна (5.5) яка описується системою рівнянь:

має асимптотично стійку частину, тобто матриця є матрицею Гурвіца.

5.3 Еквівалентна система

Позначимо Лапласове перетворення функції G(t) як

Використовуючи Лапласове перетворення, ми переписуємо замкнену систему (5.1)-(5.4), яка вміщує ПІД-НР в еквівалентну форму (ми опускаємо тут деякі алгебраїчні перетворення):

(5.7)

де

(5.8)

(5.9)

Відповідно до табл. 5.1 запишемо поліном наступним чином:

(5.10)

Перетворення системи, що вміщує ПІД-НР, як на

рис. 5.1, в модель (5.7)-(5.10), якщо задовільняється нерівність:

(5.11)

Припустимо, що система задовільняє УУГ, тобто

(5.12)

Звернім увагу, що виконання (5.12) має на увазі, що (5.11) правильна.

Отже основним результатом є наступне.

Теорема 1. Розглянемо систему, яка вміщує ПІД-нечіткий регулятор, для якого модель має форму відношень (5.1)-(5.4).

Припустимо, що задовільняються наступні умови:

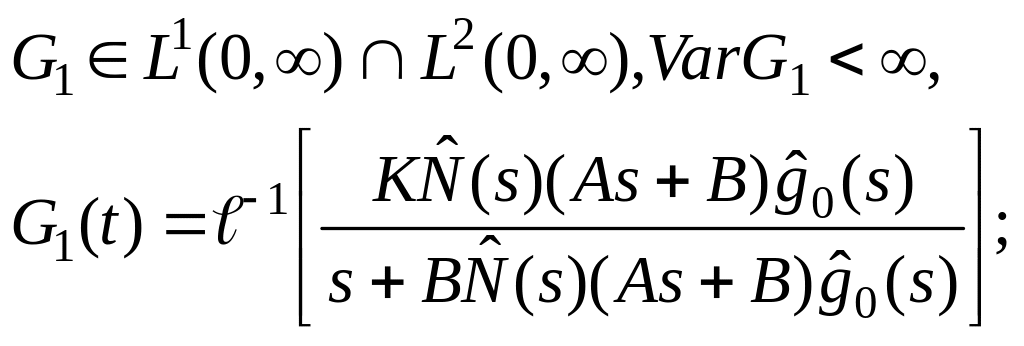1. у загальнена умова Гурвіца, дана в (4.12);

3) обмежено, і

де

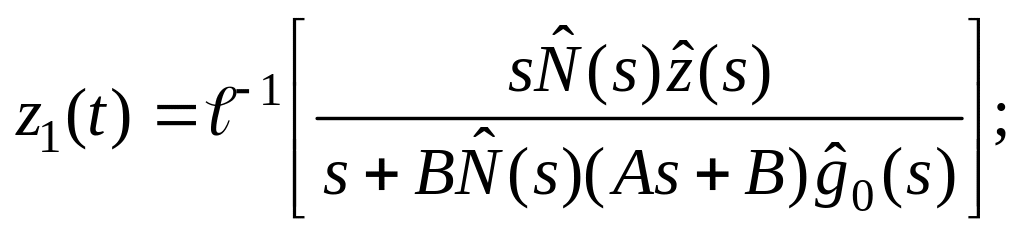
4) частотна умова

(Константи А, В: і поліном дані в табл. 5.1 для кожного типу регулятора: ПД-НР, ПІ-НР або ПІД-НР). Якщо вищевказані умови задовільняються, то помилка є така: є обмеженою

Доведення. Перше доведемо наступне.

Лема 1. Розглянемо систему, описану рівнянням

(5.13)

В цій системі функції y(t) і u(t) зв’язані між собою наступним чином:

(5.14)

Якщо умови, дані нижче

1)

2) є обмеженою, і

3) частотна умова

задовольняються, тоді існує константа С, що є незалежною від Т і z(t), така, що будь-який розв’язок системи (5.13)-(5.14) задовільняє в просторі (для ) наступну нерівність

.

Крім того, всі розв’язки у(t) є такі, що: є обмеженою, і

Доведення леми 1: Перше ми доведемо, що і константа С не залежить ні від Т ні від z(t).

Позначимо скалярний добуток і нормаль в просторі

L² (0,Т) наступним чином:

Для індекс Т в скалярному добутку або в нормалі може бути опущений. Після скалярного множення обох сторін інтегрального рівняння (5.13) на u, стосовно нерівності (5.14) ми отримаємо

(5.15)

де символ “*” означає інтеграл згортки. Вважаємо, що Оскільки то одержимо наступні нерівності

(5.16)

де . Перетворюючи нерівність (5.15) і беручи в розрахунок (5.16), ми дістанемо

,

де

Отже, отримаємо і не залежить від Т. Оскільки, то Зараз ми використаємо припущення, що імпульс відповідає і функції Крім того з рівняння (5.13) і з теореми (5.14), одержимо наступну нерівність

і отже

Розглядаючи (5.13) ми приходимо до наступної нерівності

Таким чином, , , z(t) є обмежена і і тому y(t) є також обмеженим і прямує до нуля коли .

Зараз повернемося до доведення Теореми 1. Еквівалентна система, тобто (5.7)-(5.8) відрізняється від системи, розглянутої в Лемі 1 тільки записом. Тобто в Теоремі 1 маємо у(t), z(t), G(t) і керування u(t), що знаходиться в просторі L²(0,T), сектор умови [0,K]. В системі (5.7)-(5.8) маємо e₁(t), z₁(t), і G₁(t), відповідно, і керування що знаходиться в L²(0,T) сектор умови [0,1]. Оскільки і або q₂=0, відповідно до табл. 5.1, тоді поліном має в будь-якому випадку два корені з від’ємними дійсними частинами. Функція e(t) є рішенням диференційного рівняння

Відповідно до теореми 1 ми маємо: і Очевидно, функція e(t) належить до L²(0,T), це є обмеженням, і накінець

Зауваження 1 Передавальна функція повинна не мати нуля s=0 і, крім того, не повинна бути асимптотично стійкою.

Зауваження 2 Можна застосовувати Теорему 1 для систем, які вміщують нечіткий логічний регулятор в якому вхід-вихід не нечітке відношення є функцією стану багатьох змінних. Це може бути проілюстровано нижче.

Приклад 1 Розглянемо проблему стійкості перевернутого маятника на візку, для якого лінеаризована модель вміщує чотири рівняння:

де х₁- кутове переміщення маятника,

х₃- переміщення візка,

і .

Припустимо, система стабілізована нечітким регулятором, для якого вихід u може бути звичайною функцією багатьох змінних, тобто u=f(х₁, x₂, x₃, x₄). Y є “штучний вихід” системи такий, що y(t)=Hx(t), де H=[16 0 0.05 0.3] і задовільняє сектор-тип нерівності

Завданням є обчислення величини к, для якої система стійка, тобто для Очевидно реальна система не є асимптотично стійкою. Однак це задовільняє УУГ якщо ми візьмемо іншу керуючу змінну, скажімо w(t) таку, що Після зміни власного значення, ця система робиться еквівалентною наступній

Лінійна частина має передавальну функцію “від w до y”. Умови (5.1)-(5.3) теореми 1 виконалися. Частотна умова (5.4) погоджується. Отже, дана система є стійкою для k>2.2631.

Таким чином теорема 1 дає достатні умови стійкості. Це може бути безпосередньо використано для аналізу стійкості найбільш простих, тобто “один вхід – один вихід” регуляторів, таких як П-НР, Д-НР або І-НР. Однак кращий результат може бути одержаний в такому випадку тоді, коли застосований класичний критерій Попова. Не є проблемою використання цього критерію у випадку П-НР або Д-НР регуляторів. Для І-НР треба зробити деяке перетворення початкової системи, як зроблено в цьому розділі (константа має бути більшою нуля).

Хоч в нашому прикладі установка була описана диференційними рівняннями, одержаний результат може бути використаний для найбільш загальних, тобто деяких нескінченновимірних систем .

Теорема 1 для дає деяку частотну залежність, але результат в цьому розділі є більш загальний. Потрібно, щоб передавальна функція установки не мала нуля при s=0, і крім того не повинна бути асимптотично стійкою.