4.12 Інтегральні оцінки перехідних процесів

Прямі показники якості перехідного процесу характеризують окремі його сторони. Виникає питання: чи не можна перехідний процес оцінити тільки одним узагальненням критеріїв без посереднього визначення його окремих показників? Виявляється, можна. Таким узагальненням критеріїв є інтегральна оцінка перехідного процесу.

Інтегральна оцінка являє собою певний визначений інтеграл від деякої функції перехідної основної помилки. Переважно інтегральні оцінки застосовують для слідкуючих систем, які є астатичними. В цих системах встановлена помилка при ступінчастому задаючому впливі рівна нулю, і перехідна складова помилки рівна помилці системи

.

В загальному вигляді формула для визначення інтегральної оцінки має вигляд

. (4.25)

Для простої інтегральної оцінки знаходиться інтеграл

. (4.26)

Ця оцінка може бути застосована тільки для перехідних процесів перерегулювання, коли помилка не змінює свого знаку (рис. 4.17, а). Інтеграл визначає заштриховану частину на рис. 4.17, а, яку інколи називають площиною регулювання.

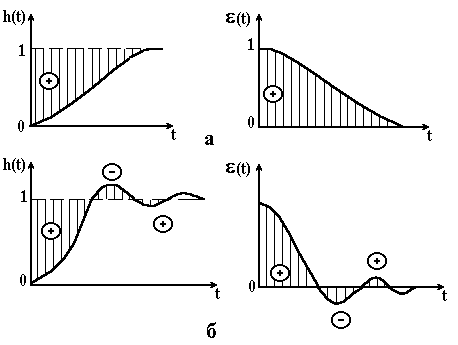
Рисунок 4.17 – Перехідна функція h(t) і помилка (t) при монотонному (а) і коливальному (б) перехідних процесах

При коливальному характері перехідного процесу оцінка не може бути застосована, так як помилка має різні знаки. В цьому випадку застосовують інтегральну оцінку (рис. 4.17, б)

, (4.27)

Вирахувати інтеграл дуже важко. Для оцінки як коливальних, так і монотонних перехідних процесів запропонована і часто застосовується квадратична інтегральна оцінка

, (4.28)

яка не залежить від знаку помилки, а отже, і від характеру кривої перехідного процесу. Інтеграл визначає заштриховану площу під кривою , яку інколи називають квадратичною площиною регулювання (рис. 4.18). Величина інтегралу буде тим менша, чим менша сума заштрихованих площин на рис. 4.18, тобто, чим більший перехідний процес до ідеальної ступінчастої видозміни регульованої величини, викликаний ступінчастою видозміною задаючого впливу.

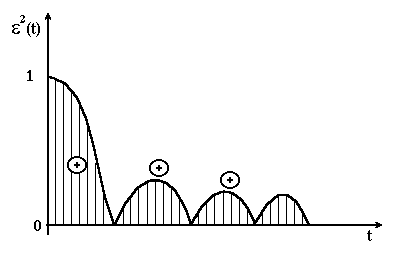
Рисунок 4.18 – Графік зміни квадрата помилки

В результаті наближення перехідного процесу до ідеального (ступінчастого) отримується велика швидкість процесу при переході регульованої величини до нового встановленого значення, що викликає велике перерегулювання. Тому при оцінці перехідного процесу за інтегралом сильно коливальний процес може видатися кращим, ніж коливальний, а це не завжди є правильним.

Квадратичну інтегральну оцінку можна покращити, якщо враховувати не тільки помилку , але й швидкість її зміни . Такою оцінкою є інтеграл

. (4.29)

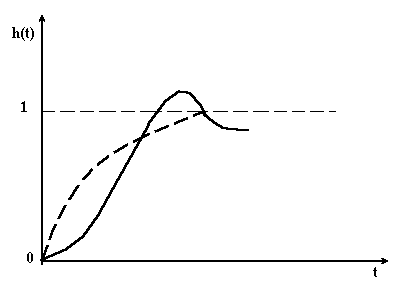
Можна довести, що мінімум інтегральної оцінки відповідає наближенню перехідного процесу не до ступінчатого, а до деякого експоненціального з постійною часу (пунктирна крива на рис. 4.19, яку називають екстремальною). Вибір параметрів системи із умови відповідає менш коливальному процесу в порівнянні з використанням квадратичної оцінки .

Рисунок 4.19 – Перехідний процес, відповідний мінімуму інтегральної оцінки І

Знаходять застосування і більш інтегральні оцінки, враховуючи помилку , а також першу , другу і більш високі похідні від . При будь-яких інтегральних оцінках якість пересічного процесу буде тим краща, чим менша величина відповідного інтегралу.

Інтегральні оцінки вираховують через коефіцієнти відображення помилки.