4.6 Оцінка стійкості автоматичної системи за її структурою

В ряді випадків оцінити стійкість автоматичної системи можна за її структурою. Це значно скорочує час, так як немає необхідності складати характеристичне рівняння.

Якщо система має таку структуру, що в ній неможливо забезпечити стійкість ні при якому значенні параметрів її елементів, то така система називається структурно-нестійкою.

Оцінимо стійкість даної системи за її структурою. Наприклад, якщо система має дві інтегруючих ланки, неохоплені жорстким зворотним зв’язком, і не має послідовно включених диференціюючих ланок, то вона буде нестійкою при будь-якому значенні параметрів її елементів.

Покажемо це на прикладі простішої системи, яка складається з однієї аперіодичної і двох інтегруючих ланок. Передавальна функція такої системи в розімкнутому стані

,

а характеристичне рівняння замкнутої системи

.

Для цього рівняння не виконується необхідна умова стійкості. Отже, система буде нестійка при будь-яких значеннях параметрів Т і К, тобто вона буде структурно нестійкою. Структурно нестійку систему можна перетворити в стійку тільки заміною її структури, тобто введенням додаткових елементів, наприклад диференціюючих елементів при включенні пропорційних елементів паралельно інтегруючим.

4.7 Синтез систем автоматичного керування, виходячи з умов стійкості

При синтезі системи автоматичного керування виникає задача вибору таких значень параметрів її елементів, при яких система буде стійкою. Щоби здійснити такий вибір, слід підставити значення параметрів, що нас цікавлять, в характеристичне рівняння системи або в передавальну функцію в загальному вигляді, тобто у вигляді літер.

Далі слід використати вибраний критерій, тобто записати умови, при яких система буде стійка. В результаті отримаємо ряд рівнянь або нерівностей, з яких визначимо значення параметрів. Нехай характеристичне рівняння системи має вигляд

.

Потрібно визначити значення постійної часу Т, при яких система буде стійкою.

Використаємо критерій Вишнеградського, отримаємо три нерівності

; (4.9)

; (4.10)

. (4.11)

З нерівності (4.11) знайдемо . При цьому значенні Т нерівності (4.9) і (4.10) також виконуються. Отже, при будь-яких система буде стійкою.

Як можна спростити розв’язок задачі синтезу, виходячи з умов стійкості? Для цього необхідно знати, які фактори викликають нестійкість системи. Одним з найважливіших факторів є великий коефіцієнт підсилення розімкненої системи. В цьому легко впевнитись, використовуючи, наприклад, критерій Найквіста-Михайлова.

Нехай передавальна функція розімкнутої системи має вигляд , де і – поліноми від р, вільні члени яких рівні одиниці; К – коефіцієнт підсилення розімкнутої системи.

АФЧХ розімкнутої системи, отриманої з передавальної функції заміною р на j , має вигляд

.

Збільшення коефіцієнта підсилення К збільшує модуль АФЧХ, тому точка перетину АФЧХ з дійсною віссю переміщується вліво, і система в кінці кінців може перетворитись зі стійкої в нестійку (рис. 4.2, а).

Як це пояснити з фізичної точки зору? При великому коефіцієнті підсилення вихідний сигнал розімкнутої системи, що при замиканні подається на вхід системи, значно переважає попередньо поданий вхідний сигнал. Система підсилює цей сигнал, і він знову подається на вхід. Процес наростає лавиноподібно, і система швидко виходить з початкового встановленого стану.

Завдання синтезу систем значно полегшується, якщо побудувати області стійкості в площині тих параметрів, які необхідно вибрати. Побудова областей стійкості особливо зручна, якщо число варійованих параметрів рівне двом. Області стійкості включають в себе ті значення шуканих параметрів, при яких синтезована система буде стійкою.

Визначення межі областей стійкості для двох параметрів проводиться принципово так само, як і при виборі одного параметра, який ми розглянули вище.

Для цього в характеристичному рівнянні або в передавальній функції системи ті параметри, що нас цікавлять, записують в загальному вигляді, тобто у вигляді літер. Потім на основі вибраного критерію записують умови знаходження системи на межі стійкості. З цією метою нерівності записують у вигляді рівнянь. Використання нерівностей в подальшому дозволить відрізнити області стійкості від областей нестійкості. На основі рівнянь будують криві або прямі в площині параметрів. Ці криві штрихують так, щоби штриховка була направлена в той бік півплощини, точки якої задовольняють даній умові стійкості. Областями стійкості будуть ті області, штриховка меж яких направлена в один бік (область А на рис. 4.6).

Рисунок 4.6 – До визначення області стійкості в площині параметрів:  і 

Для прикладу побудуємо області стійкості в площині параметрів Т і К для системи, характеристичне рівняння якої

.

Граничні криві будуть мати вигляд (на рис. 4.7, криві відповідно 2, 1, 4 і 3)

; (4.12)

; (4.13)

; (4.14)

, (4.15)

а умови стійкості – відповідно

,

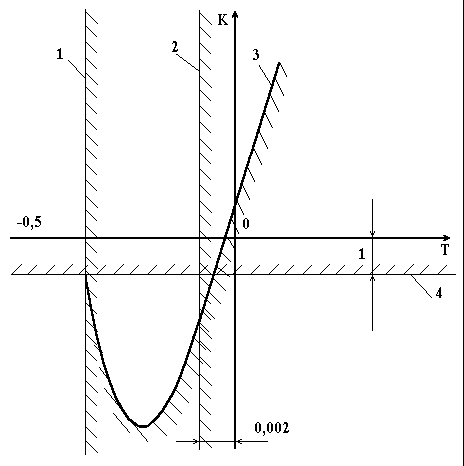
Рисунок 4.7 – До визначення меж області стійкості в площині параметрів Т і К

З рис. 4.7. видно, що областю стійкості буде частина площини К, Т, яка розміщена в першому квадранті і йде від граничної прямої 4 вверх, а від граничної кривої 3 – вправо.

Принципово такими ж будуть межі областей стійкості при використанні інших критеріїв стійкості. Слід зазначити, що побудова областей стійкості в площині параметрів значно простіша при використанні алгебраїчних критеріїв та критерію Михайлова, ніж при використанні частотних критеріїв.

Дуже важливо визначити, які значення параметрів системи доцільно вибирати, якщо в розпорядженні є області стійкості, побудовані в площині цих параметрів. На перший погляд здається, що значення параметрів можуть бути будь-якими, лиш би вони належали області стійкості. Але це не так. Якщо взяти значення параметрів, близькі до межі області стійкості, то на практиці може статись, що в результаті звичайної неточності виготовлення системи або в результаті зміни параметрів в процесі експлуатації їх значення можуть бути такими, що не відповідатимуть області стійкості системи. Система стане нестійкою і, отже, непридатною до експлуатації.

Щоби усунути можливість виникнення нестійкості системи, вводять запас її стійкості.