3.8 Ланка запізнення

Ланка запізнення – це ланка, вихідна величина якої така сама, як і вхідна, але зсунута на величину чистого запізнення  (рис. 3.23).

Передавальну функцію цієї ланки визначають, користуючись виразами для вхідного і вихідного сигналів, перетворених за Фур’є

Тоді АФХ

Отже,

.

Рисунок 3.23 – Перехідна характеристика ланки запізнення

Запишемо передавальну функцію

Якщо ланка запізнення має передавальний коефіцієнт, що відрізняється від одиниці, тобто , то

.

Взагалі, запізненням володіють такі ланки, які мають різні властивості. Наприклад: – інерційна ланка І-го порядку.

Такі ланки представляють у вигляді двох послідовно з’єднаних ланок.

Рисунок 3.24 – АФХ (а), АЧХ (б) і ФЧХ (в) ланки запізнення

Рисунок 3.25 – Перехідна характеристика інерційної ланки І-го порядку

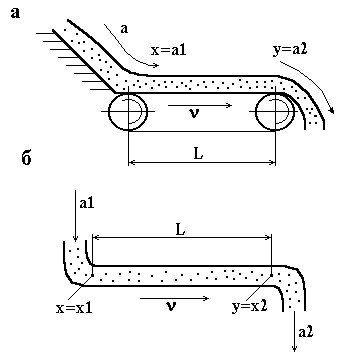
Найбільш характерним прикладом ланки запізнення є: стрічковий живильник (рис. 3.26, а), що транспортує сипкий матеріал (руду, концентрат). Запізнення  (с) між кількістю матеріалу (кг/с), який викидається в одиницю часу на живильник матеріалу (кг/с) на спуску живильника залежить від довжини L (м) і швидкості руху v (м/с)

. (3.81)

Другим розповсюдженим прикладом ланки запізнення є трубопровід (рис. 3.26, б), по якому в технічний об’єкт керування рідка речовина (пульпа, розчин реагенту) в кількості (м³/с) з концентрацією корисного компоненту

(кг/м³).

Зазначимо, що необхідність розглядати живильник, трубопровід та інші транспортуючі пристрої як ланки запізнення виникають лише в тих випадках, коли вони є елементами замкнутих автоматичних систем керування.

Таким чином, ланка запізнення відзначається наступними характерними особливостями:

1. Вона передає будь-які вхідні сигнали без спотворення їх форми, але затримує на інтервалі  в сталому режимі (при ) вихідний сигнал.

. (3.82)

Як і для інших статичних (позиційних) ланок, передавальна функція ланки

Рисунок 3.26 – Ланки з запізненням

. (3.83)

2. За властивостями АЧХ ланка запізнення еквівалентна безінерційній: пропускає високочастотні і низькочастотні сигнали з однаковим відношенням амплітуд (рівним одиниці).

3. За властивостями ФЧХ вона еквівалентна інерційним ланкам: створює від’ємний зсув (пропорційний запізненню  і частоті ).

4 Стійкість автоматичних систем і показники якості перехідних процесів

4.1 Поняття стійкості автоматичних систем керування

Вияснимо фізичне трактування поняття стійкості. Роглянемо кулю, поміщену у верхню точку підвищення. Вона знаходиться в нестійкому положенні. Дійсно, достатньо найменшого відхилення кулі від початкового положення, як вона скотиться по схилу поверхні і не повернеться у вихідне положення.

Навпаки, куля, що знаходиться у впадині, займає стійке положення, і після відхилення вона обов’язково повернеться до свого початкового положення.

Таким чином, стійкість – це властивість системи (куля – поверхня) повертатись у вихідний стан після виведення її з цього стану та припинення дії збурення.

Як видно з визначення, здатність системи повертатись в початковий стан пов’язується з початковими відхиленнями. В розглянутих прикладах стійкість і нестійкість не залежать від початкових відхилень кулі. Але можна уявити собі таку систему, яка при малому відхиленні повертається, а при великому – не повертається у вихідне положення. Прийнято вважати, що така система стійка в малому і нестійка у великому, оскільки стійкість пов’язана з величиною початкового відхилення. Система, з кулею, що знаходиться у впадині є безмежно стійкою, так як куля буде повертатись у вихідне положення при будь-якому початковому відхиленні. Система має властивості байдужої рівноваги.

Чи завжди за вихідний стан системи, стійкість якої оцінюється, беруть стан спокою? Ні, не завжди. В загальному випадку можна говорити про стійкість руху взагалі, тобто руху, пов’язаного з будь-яким переміщенням маси або енергії. Наприклад, можна оцінити стійкість руху супутника, як його здатність повертатись на вихідну орбіту після припинення дії сил, які відхиляли супутник від заданої орбіти. Так само можна оцінити стійкість системи автоматичного управління, як її здатність повертатись до початкового незбуреного руху після припинення дій збурення.

Отже, ми розглянули якісну оцінку поняття стійкості. Але існує і кількісна оцінка цього поняття: стійкість можна описати математичними формулами.

Вперше найбільш суттєві математичні результати по стійкості механічних систем були отримані харків’янином А.М.Ляпуновим у 1880-1910 рр. Оскільки різні за своєю природою матеріальні системи описуються однаковими диференціальними рівняннями, то результати по стійкості механічних систем, отримані А.М.Ляпуновим, можна використати і до інших фізичних систем, в тому числі до систем автоматичного керування.

Стійкість є дуже важливою характеристикою якості систем і пристроїв, що використовуються в різних галузях техніки. Особливо гостро проблема стійкості стоїть в автоматиці. Це пояснюється наступним. Автоматичні системи є замкнутими системами, в яких вихідна величина через основний зворотний зв’язок подається на вхід системи, де порівнюється з заданим впливом. Система, що нормально функціонує, бажає зменшити різницю між значеннями задаючого впливу і керуючої величини. Але інколи виходить так, що ця різниця буде не зменшуватись, а зростати з плином часу, тобто система буде нестійкою. Характерно, що нестійкою може бути система, яка складається тільки зі стійких елементів, як це часто буває на практиці.

Через складність автоматичних систем для оцінки їх стійкості тільки фізичних уявлень недостатньо. Для цього необхідне використання математичного апарата. Тому розглянемо, в чому полягає особливість математичного трактування стійкості автоматичних систем.