3.6 Диференціююча ланка

Диференціюючою називають таку ланку, в якій вихідна величина пропорційна похідній від вхідної величини

. (3.48)

Перетворимо рівняння (3.48) за Лапласом

тоді

Знаходимо перехідну функцію ланки, перехідна характеристика якої показана на рис. 3.10

.

Амплітудно-фазова функція

.

АФХ співпадає з уявною віссю (рис. 3.11).

АЧХ:

ФЧХ:

ЛАЧХ:

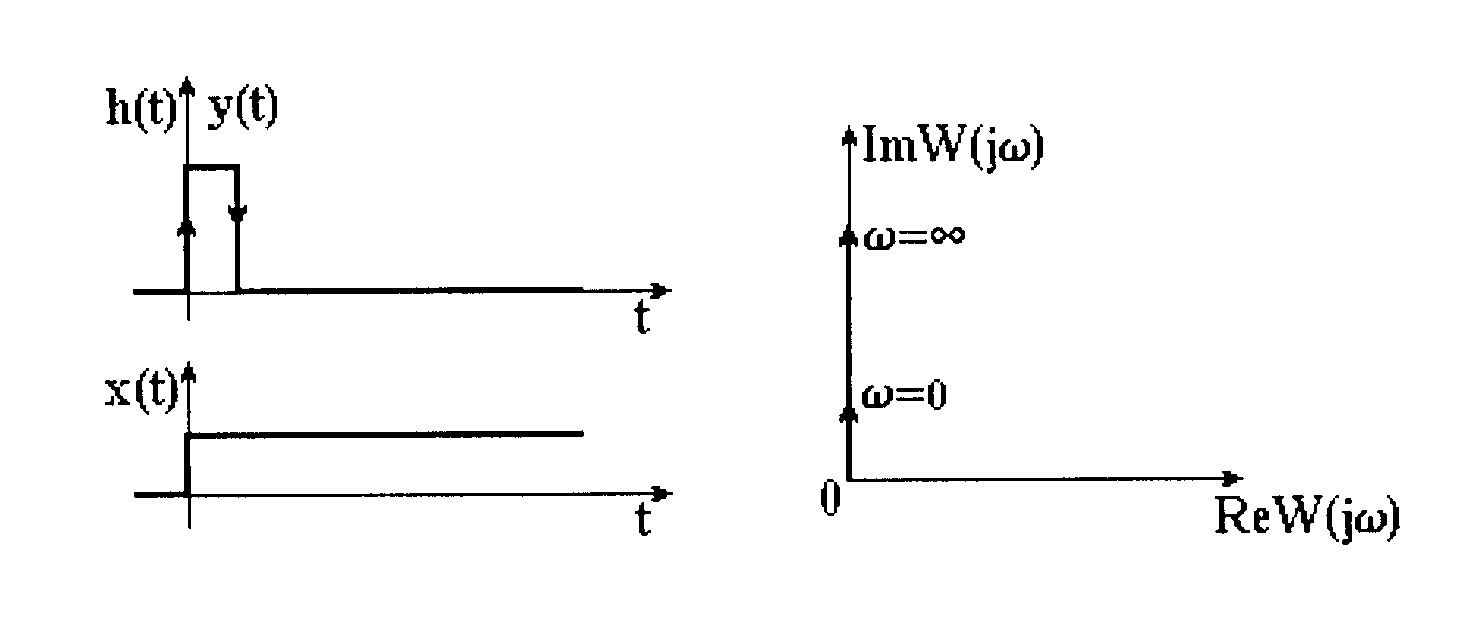
Рисунок 3.10 – Перехідна характеристика диференціюючої ланки

Рисунок 3.11 – АФХ диференціюючої ланки

Реальна диференціююча ланка являє собою послідовне з’єднання ідеальної диференціюючої ланки та інерційної ланки І-го порядку. Вона має таке диференціальне рівняння:

Рисунок 3.12 – АЧХ (а), ФЧХ (б), ЛАЧХ (в) диференціюючої ланки

(3.49)

і передавальну функцію

. (3.50)

Таку ланку можна зобразити у вигляді послідовного або паралельного з’єднання безінерційної і інерційної ланок (рис. 3.13).

Характеристики реальної диференціюючої ланки приведені на рисунку 3.14.

Приклади реальних диференціюючих ланок приведені на рисунку 3.15.

Диференціюючі ланки в статичному режимі не передають сигналу на вихід, вони добре пропускають високочастотні сигнали і погано-низькочастотні. Вони вносять додатковий фазовий зсув.

Рисунок 3.13 – Реальні диференціюючі ланки

Рисунок 3.14 – Характеристики реальної диференціюючої ланки

Рисунок 3.15 – Приклади диференціюючих ланок

3.7 Інерційні ланки другого порядку

Диференціальне рівняння ланок ІІ-го порядку має вигляд

. (3.51)

Йому відповідає рівняння динаміки в операторній формі

(3.52)

і передавальна функція

. (3.53)

Характеристичне рівняння має два корені

. (3.54)

Характер перехідного процесу залежить від типу коренів, які можуть бути дійсними, комплексними і уявними.

Рисунок 3.16 – Перехідна характеристика аперіодичної ланки ІІ-го порядку

І. Якщо , то обидва корені дійсні, тобто

де і – умовні постійні часу.

Перехідна характеристика такої ланки є монотонною. Вона близька до інерційної ланки І-го порядку, тому її називають – аперіодична ланка ІІ-го порядку.

При передавальну функцію (3.53) можна представити в таких еквівалентних формах:

, (3.55)

, (3.56)

яким відповідають алгоритмічні схеми, приведені на рисунку 3.17, б, г.

ІІ. Якщо , то корені характеристичного рівняння комплексні і спряжені

(3.57)

Перехідна характеристика в цьому випадку носить коливальний характер (рис. 3.18). Тобто, маємо коливальну ланку.

ІІІ. Якщо , то обидва корені уявні, і перехідна характеристика являє собою незатухаючу синусоїду. Інерційну ланку ІІ-го порядку з називають ідеальною коливальною або консервативною.

Поряд із загальними властивостями всі ланки реально відрізняються одна від одної. Розглянемо окремо характеристики інерційних ланок ІІ-го порядку.

Перехідна функція аперіодичної ланки ІІ-го порядку може бути одержана додаванням загального рішення

(3.58)

Рисунок 3.17 – Алгоритмічні схеми інерційних ланок ІІ-го порядку

і рішення, яке відповідає примусовій складовій при тоді перехідна функція має такий вигляд:

. (3.59)

Після підстановки початкових умов і у вираз (3.59), маємо

(3.60)

Рисунок 3.18 – Перехідна характеристика коливальної ланки	Рисунок 3.19 – Перехідна характеристика консервативної ланки

тоді перехідна функція має такий вигляд:

. (3.61)

Передавальна функція

. (3.62)

Сталі часу і можна визначити на підставі графікоекспериментальної перехідної характеристики.

Характеристики аперіодичної ланки ІІ-го порядку показані на рис 3.21.

З частотних характеристик даної ланки випливає, що вона добре пропускає сигнали низької частоти і погано пропускає сигнали високої частоти.

Коливальна ланка – це така ланка, в якій при стрибкоподібній зміні вхідної величини вихідна величина прямує до нового встановленого значення, здійснюючи навколо нього затухаючі коливання.

Для більш детального вивчення диференціальне рівняння ланки записують у такому вигляді:

, (3.63)

Рисунок 3.20 – Перехідна характеристика аперіодичної ланки ІІ-го порядку

де – постійна часу, яка характеризує інерційність ланки; де – відносний коефіцієнт затухання; він характеризує коливальність ланки і змінюється від 0 до 1.

Перетворивши рівняння (3.63) за Лапласом, отримаємо передавальну функцію

, (3.64)

. (3.65)

Ця передавальна функція вигідніша, бо тут фігурує одна постійна часу Т. Прирівнюючи до нуля знаменник (3.65), одержимо характеристичне рівняння

Рисунок 3.21 – Характеристики аперіодичної ланки ІІ-го порядку

. (3.66)

Розв’язуючи це рівняння відносно р, будемо мати

, (3.67)

де – коефіцієнт затухання; – кутова частота затухання коливань, рад/с.

Підставляючи в загальний розв’язок диференціального рівняння (3.58) значення комплексних коренів (3.67) і додавши до нього часткове рішення , отримаємо перехідну функцію коливальної ланки

, (3.68)

За допомогою формули Ейлера

(3.69)

функцію (3.68) можна перетворити до такого вигляду:

. (3.70)

Використовуючи початкові умови і , знайдемо

, (3.71)

. (3.72)

Остаточно перехідна функція може бути записана в наступному вигляді:

. (3.73)

Вільна складова перехідної функції (рис. 3.22, а) являє собою синусоїду, амплітуда якої зменшується за законом експоненти.

Період затухаючих коливань дорівнює

. (3.74)

Чим менша постійна часу Т і чим більший коефіцієнт демпфування , тим швидше затухають коливання. Якщо коефіцієнт демпфування , що відповідає , то на виході ланки після подачі одиничного ступінчатого впливу виникають незатухаючі коливання з частотою .

Швидкість затухання коливального перехідного процесу оцінюють степенем затухання

. (3.75)

Рисунок 3.22 – Характеристики коливальної ланки ІІ-го порядку

Чим ближче до одиниці, тим швидше затухають коливання. Степінь затухання залежить від співвідношення дійсної і уявної частин комплексного кореня. Дійсно, якщо у вираз (3.73) підставити два значення t, які відрізняються на період затухання коливань , то можна отримати

. (3.76)

Відношення називають ступенем коливальності.

Використовуючи вираз (3.67), можна з’ясувати зв’язок між ступенем коливальності  і коефіцієнтом демпфування 

. (3.77)

Від коефіцієнта  залежить максимальне значення перехідної функції.

Продиференціювавши (3.70) за t і прирівнявши похідну до нуля, одержимо

, (3.78)

. (3.79)

АФХ коливальної ланки (рис. 3.22, е) описується функцією

. (3.80)