3.5 Інтегруючі ланки

Розрізняють два види інтегруючих ланок: ідеальні і реальні. Загальною особливістю інтегруючих ланок є пропорційність похідної вихідної величини моментальному значенню вхідної величини. Причому, в ідеальній інтегруючій ланці пропорційність існує в будь-який момент часу після подачі ступінчатої дії, а в реальній – тільки після завершення процесу в ланці.

Диференціальне рівняння ідеальної інтегруючої ланки

. (3.33)

Коефіцієнт пропорційності k залежить від конструктивних параметрів ланки і має розмірність

. (3.34)

Рівнянню (3.33) рівносильне інтегральне співвідношення

, (3.35)

яке в даній формі виражає залежність вихідної величини від вхідної і пояснює назву ланки: ланка інтегрує вхідний сигнал.

Підставляючи у співвідношення (3.34) , можна одержати перехідну функцію

. (3.36)

Графік функції показаний на рис. 3.8, а (лінія 1). Імпульсна перехідна функція ланки

. (3.37)

Передавальна функція ідеальної інтегруючої ланки

. (3.38)

Амплітудно-фазова характеристика ланки

(3.39)

на комплексній площині зображується у вигляді прямої, яка співпадає з уявною віссю (рис. 3.8, б – лінія 1).

Амплітудна частотна характеристика

Рисунок 3.8 – Характеристики інтегруючих ланок

(3.40)

являє собою гіперболу (рис. 3.8, в, лінія 1), яка при прямує до нескінченності. Цю особливість можна умовно (за аналогом зі статичними ланками) пояснити наявністю передавального коефіцієнта, рівного нескінченості.

При збільшенні частоти значення прямує до нуля. Ця властивість зближує інтегруючі ланки з інерційними.

Фазова частотна характеристика ідеальної інтегруючої ланки

(3.41)

показує, що зсув фаз, який породжується ланкою, на всіх частотах однаковий і рівний -90 (рис. 3.8, г, лінія 1).

Логарифмічна амплітудна характеристика

(3.42)

являє собою пряму з нахилом – 20 дБ/дек, яка проходить через точку з координатами

Розглянемо тепер характеристики реальної інтегруючої ланки. Її диференціальне рівняння

, (3.43)

а передавальна функція

. (3.44)

Неважко побачити, що ланка з передавальною функцією (3.43) може розглядатись як послідовне з’єднання двох елементарних ланок: ідеальної інтегруючої з передавальною функцією і статичної інерційної ланки першого порядку зі сталою часу Т і передавальним коефіцієнтом, рівним одиниці. Тому всі частотні характеристики реальної інтегруючої ланки можуть бути одержані за характеристиками цих простих ланок та відповідними правилами перемножування комплексних (векторних) величин.

Характеристики реальної інтегруючої ланки показані на рис. 3.8 (лінія 2).

Інтегруючими ланками є виконуючі двигуни і механізми – прилади, які переміщують виконавчі органи (шибери, заслінки, вентилі і т. д.). Їх називають також серводвигунами і сервомеханізмами. Вхідною величиною цих приладів служить, звичайно, кількість енергії або речовини, яка поступає в прилад, а вихідною – лінійне або кутове переміщення будь-якого елемента. Ступінь ідеальності (безінерційності) таких інтегруючих ланок залежить від величини мас частин, які переміщуються (обертаються) навколо виконавчого приладу і приведеного ним в рух виконавчого органу.

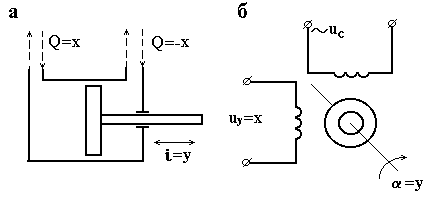
Ідеальною інтегруючою ланкою можна вважати (з деякими припущеннями) гідравлічний виконавчий механізм (рис. 3.9, а), вхідною величиною якого є кількість рідини Q (м³/с), що поступає в одиницю часу в порожнину циліндра, а вихідною – переміщення l (м) поршня з штоком. Дійсно, якщо маса частин, що переміщуються, мала і якщо зусилля, породжене тиском гідронасоса, істотно більше сил опору, то переміщення поршня визначається рівнянням балансу рідини

, (3.45)

де S – площа поршня, м².

Рисунок 3.9 – Приклади інтегруючих ланок

Рівняння (3.45) легко приводиться до рівняння (3.33) або (3.35). Коефіцієнт k в даному випадку рівний . Його розмірність або 1/м².

Властивостями ідеальної інтегруючої ланки володіє при деяких умовах інерційна ланка першого порядку. Наприклад, аперіодичний rc-ланцюг при частотах вхідної дії може приблизно розглядатись як інтегруюча ланка. Дійсно, якщо в частотній функції (3.19) знехтувати одиницею в знаменнику, то вона співпадає з функцією (3.39).

Реальними інтегруючими ланками є електричні виконавчі двигуни постійного і змінного струмів. На рис. 3.9, б зображений двофазний асинхронний двигун. Його вхідна величина – напруга змінного струму , прикладена до обмотки керування, вихідна – кут повороту вала , град. Діюче значення напруги на обмотці збудження вважається незмінним. При деяких припущеннях (інерційність обмотки управління мала, статичні механічні характеристики двигуна попередньо лінеаризовані, діапазон зміни напруги обмежений) двигун може бути описаний передавальною функцією (3.44). Передавальний коефіцієнт двигуна приблизно може бути розрахований через номінальні значення частоти обертання , 1/с і керованої напруги

, град./(Вс) . (3.46)

Стала часу залежить від приведеного на вал двигуна моменту інерції частин, що обертаються J, кгм³

, с, (3.47)

де М_П – номінальне значення пускового моменту, Нм.