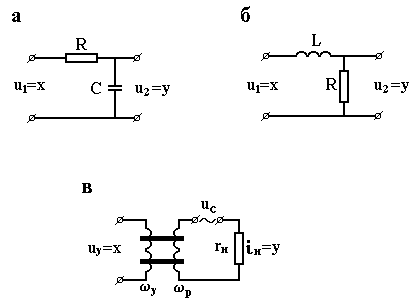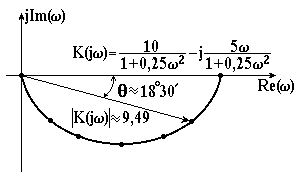3.4 Інерційна ланка і-го порядку

Диференціальне рівняння ланки має вигляд

, (3.14)

де k – передавальний коефіцієнт, який характеризує властивості ланки в статичному режимі; Т – стала часу, яка характеризує інерційність ланки.

Перехідну функцію ланки можна знайти, як суму загального і часткового розв’язків рівняння. Використовуючи відому методику, одержимо наступний вираз для перехідної функції:

. (3.15)

Графік перехідної функції зображений на рис. 3.4, а. За допомогою методів аналітичної геометрії неважко переконатися в тому, що дотична до кривої в точці відсікає на горизонтальній прямій відрізок, рівний сталій часу Т. Перехідна функція при рівна , а при функція досягає значення . В приблизних розрахунках зазвичай вважають, що при перехідний процес практично закінчився.

Рисунок 3.4 – Характеристика інерційної ланки І-го порядку

Імпульсна перехідна функція ланки може бути одержана шляхом диференціювання функції . Для інерційної ланки першого порядку імпульсна функція має вигляд

. (3.16)

Застосовуючи до лівої і правої частин рівняння перетворення Лапласа, одержимо рівняння динаміки ланки в операційній формі

. (3.17)

З рівняння (3.17) знаходимо передавальну функцію ланки

. (3.18)

Підставляючи в передавальну функцію , одержимо амплітудно-фазову функцію

. (3.19)

Перемножуючи чисельник і знаменник функції на вираз , спряжений із знаменником, можна позбутися величини j в знаменнику і представити амплітудно-фозову функцію у вигляді суми дійсної і уявної частин

, (3.20)

де

(3.21)

Вираз (3.21) можна розглядати як рівняння амплітудно-фазові характеристики , задане в параметричній формі в системі координат і . Роль третьої змінної (параметра) відіграє частота .

Якщо виразити уявну складову через дійсну , тоді можна переконатись, що амплітудно-фазова характеристика являє собою півколо з центром в точці і з діаметром, рівним k (рис. 3.4, б).

Розподілення точок, які відповідають різним значенням , вздовж кривої залежить від величини сталої часу Т. На графіку показані характерні точки , і .

Вираз для амплітудної частотної характеристики можна одержати за формулами (5.120) або (5.123).

Для розглянутої ланки простіше використати формулу (5.123)

. (3.22)

Графік функції зображений на рис. 3.4, в. З графіка видно, що гармонічні сигнали малої частоти ( ) пропускаються ланкою з відношенням амплітуд вихідної і вхідної величин, близьких до передавального коефіцієнта k. Сигнали великої частоти ( ) погано пропускаються ланкою відношення амплітуд істотно менше від коефіцієнта k. Чим більша стала часу Т, тобто, чим більша інерційність ланки, тим менша характеристика , витягнута вздовж осі частот, або, як прийнято говорити в автоматиці, тим вужча смуга пропускання частот. В практичних розрахунках ширину смуги пропускання ланок і систем визначають за ординатою , рівний . Для інерційної ланки першого порядку

. (3.23)

Графік функції (3.23) показаний на рис. 3.4, г. Чим більша частота вхідного сигналу, тим більше відставання по фазі вихідної величини від вхідної. Максимально можливе відставання рівне 90. При частоті зсув фаз рівний 45.

Розглянута ланка є мінімально-фазовою. Фазовий зсув, який створює ця ланка, менший, ніж в будь-якій іншій ланці з такою ж амплітудною характеристикою. Наприклад, у нестійкій інерційній ланці першого порядку

(3.24)

амплітудна характеристика не відрізняється від характеристики (3.22), а фазова згідно з формулою (5.121) рівна

. (3.25)

При зміні частоти від 0 до + фазовий зсув змінюється від -180 до -90.

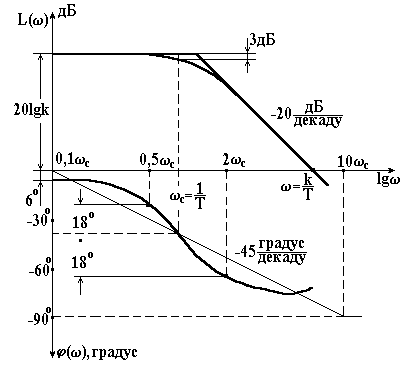
Розглянемо тепер логарифмічні частотні характеристики ланки. Логарифмічна амплітудна характеристика

. (3.26)

Крива, яка точно відповідає функції (3.26), показана на рис. 3.5 тонкою лінією. В практичних розрахунках використовують наближену характеристику , яка являє собою ламану у вигляді двох асимптот.

Перша асимптота (низькочастотна) одержується при малих частотах, коли величиною у виразі (3.26) можна знехтувати і прийняти, що

. (3.27)

Низькочастотна асимптота від частоти не залежить і являє собою пряму, паралельну до осі частот і віддалену від неї на відстань .

Друга асимптота (високочастотна) замінює точну характеристику при великих частотах, коли і одиницю під коренем у формулі (3.26) можна не враховувати. Вираз для цієї асимптоти

. (3.28)

Ця асимптота залежить від частоти. В логарифмічній системі координат вона являє собою пряму, яка має негативний

Рисунок 3.5 – Логарифмічні частотні характеристики інерційної ланки І-го порядку

нахил і проходить через точку з координатами , . Підставляючи у формулу (3.28) два значення частоти і , можна переконатись, що приріст високочастотної асимптоти, яка припадає на одну декаду, рівна – 20 дБ.

Значення спряженої частоти , при якій перетинаються обидві асимптоти, знайдемо з умови

, (3.29)

звідси

. (3.30)

Наближена амплітудна характеристика інерційної ланки першого порядку показана на рис. 3.5 жирною лінією. Можна довести, що найбільша помилка від наближеної заміни одержується при спряженій частоті. Ця помилка рівна 3 дБ.

Фазова частотна характеристика (рис. 3.5, тонка лінія) в системі координат також може бути замінена наближеною характеристикою, яка на інтервалі частот від до являє собою пряму, яка має нахил –45 град./дек. і проходить через точку . Максимальна помилка, яка при цьому допускається, не перевищує 6.

Інерційними ланками першого порядку є конструктивні елементи, які можуть накопичувати енергію і які володіють так званими властивостями самовирівнювання. Найпростішим прикладом такого елемента служить електричний пасивний чотириполюсник (рис. 3.6, а), що складається з резистора опором r, Ом і конденсатора ємністю С, Ф. Вихідна величина чотириполюсника – напруга – після подачі на його вхід постійної напруги змінюється пропорційно величині заряду, що накопичується в ємності. В перші моменти заряд зростає швидко (рис. 3.4, а), а потім в міру наближення на обмотках конденсатора до вхідної напруги струм заряду зменшується, а швидкість зростання напруги поступово спадає до нуля.

Рисунок 3.6 – Приклади інерційних ланок І-го порядку

Параметри передавальної функції (3.18) в чотириполюснику, що розглядається, рівні: , , с.

Властивостями інерційної ланки першого порядку володіють також електричні елементи з індуктивностями L, Г, в яких вихідний сигнал пропорційний струму через індуктивність. Найпростішим прикладом такого роду є ланцюг, зображений на рис. 3.6, б. Передавальний коефіцієнт ланцюга , а стала часу , с.

Більш складним прикладом ланки такого порядку є магнітний підсилювач, який широко використовується в автоматичних системах. На рис. 3.6, в зображена схема найпростішого магнітного підсилювача, так званого дроселя насичення. Його використовують для регулювання струму в ланцюгу активного або пасивного навантаження. Якщо як вхідну величину підсилювача розглядати напругу постійного струму , що подається на обмотку керування, а як вихідну – діюче значення струму в ланцюгу активного навантаження, тоді підсилювач наближено описується передавальної функцією (3.18). Передавальний коефіцієнт підсилювача в такому випадку рівний

, (3.31)

а стала часу

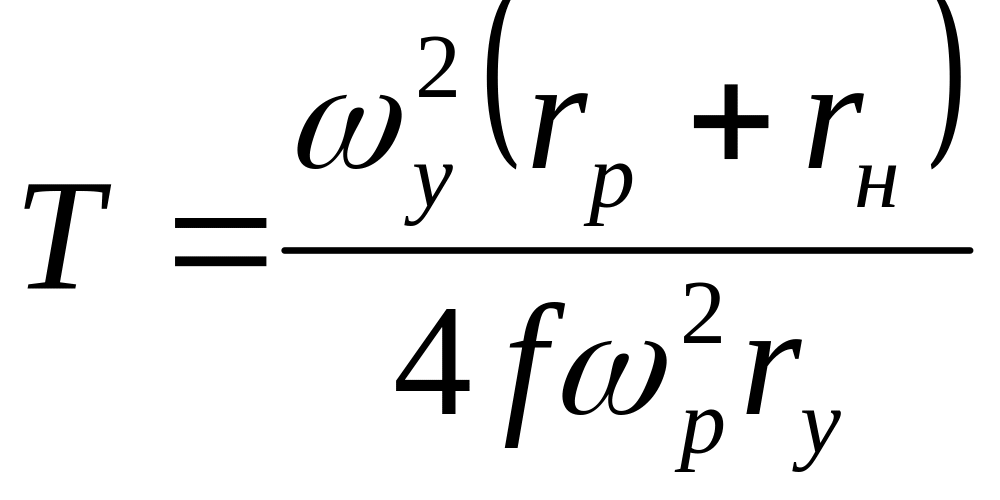, (3.32)

де – число витків відповідно обмотки керування і робочої обмотки; – опір відповідно обмотки керування, робочої обмотки і навантаження; f – частота напруги мережі.

Магнітні підсилювачі більш складних типів також можуть бути наближено описані передавальною функцією (3.18), але параметри k і Т необхідно визначити експериментально або вирахувати за формулами, які можна знайти в спеціальних довідниках для магнітних підсилювачів.

Приклад. Побудувати амплітудно-фазову характеристику стійкої аперіодичної ланки при значеннях: коефіцієнт підсилення і стала часу ланки .

Підставляючи ці значення в рівняння передавальної функції ланки, одержимо

.

Зробивши заміну , одержимо рівняння амплітудно-фазової характеристики

.

Позбавившись уявності в знаменнику, одержимо

.

Тут дійсна частина

і уявна частина

.

Для побудови амплітудно-фазової характеристики будемо змінювати частоту  від нуля до нескінченності

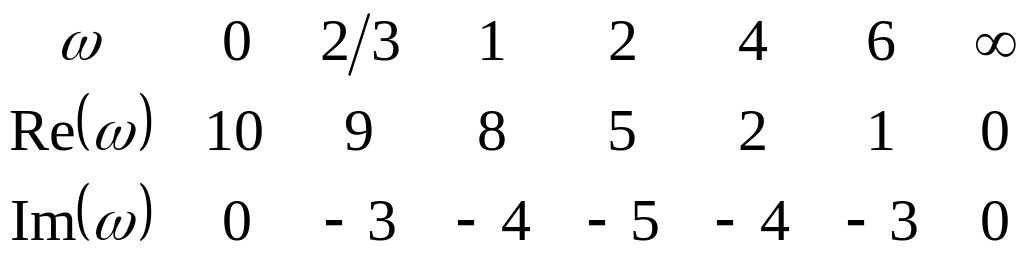
За одержаними значеннями будуємо апмлітудно-фазову характеристику (рис. 3.7) – півколо, яке проходить через початок координат, який опирається на дійсну вісь, як на діаметр, і розміщений в четвертому квадранті.

Напишемо це рівняння в полярних координатах

.

Рисунок 3.7 – Амплітудно-фазова характеристика стійкої аперіодичної ланки І-го порядку

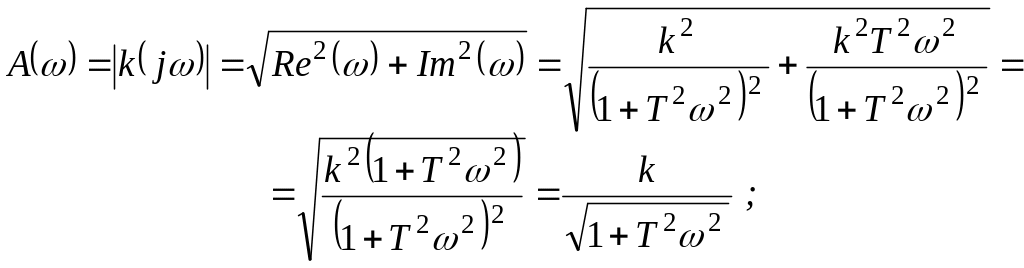
Для побудови графіка амплітудно-фазової характеристики будемо змінювати величину  від нуля до нескінченності. Знайдемо крайні точки графіка

тобто в цьому випадку ми одержали невизначеність, яку розкриємо, використовуючи правило Лопіталя

.

Отже,

.

Одержані точки лежать: одна на осі реальних, а інша – в початку координат і обмежують графік амплітудно-фазової характеристики, яка являє собою півколо з радіусом, рівним , розміщене в четвертому квадранті, що опирається на дійсну вісь, як на діаметр, і проходить через початок координат комплексної площини.

Для перевірки цього припущення досить визначити ординату цього півкола. Абсциса точки центра півкола

.

Звідки

.

Підставляючи значення  у вираз для ординати точки центра півкола, одержимо

,

тобто ордината точки центра півкола дійсно рівна його радіусу, що треба було довести.