1.6 Вплив напруги живлення на режим гзз

Вплив амплітуди напруги збудження U_тб. Залежності колекторного струму І_к1 від напруги збудження при фіксованих значеннях зсуву на базі Е_б=const називаються коливальними характеристиками. Нехай Е_б = Е'. Тоді кут відсічення колекторного струму рівний 90 градусів і не залежить від амплітуди змінної напруги на вході. При малих амплітудах каскад знаходиться в недонапруженому режимі (Н.Р.), струм наростає майже лінійно до тих пір, поки не наступить критичний режим. При цьому наступить обмеження струму, а з переходом в перенапружений режим (П.Р.) струм зменшується (мал. 1.14, крива 1). Лінійно наростаючу ділянку цієї характеристики використовують при посиленні модульованих коливань.

Мал. 1.14 – Коливальні характеристики

При Е_б < Е' коливальна характеристика приведена на мал. 1.14 (крива 2).

Вплив напруги зсуву на базі Е_б. Залежності струмів і напруги від зсуву на базі називаються статичними модуляційними характеристиками (СМХ) при базовій модуляції зсувом. Вони приведені на мал. 1.15. Видно, що в недонапруженому режимі існує достатньо протяжна ділянка, де залежність І_к1 = ƒ(Е_б) близька до лінійної. Ця ділянка використовується на практиці для формування амплітудно-модульованих коливань.

Мал. 1.15 – Статистичні модулюючі характеристики при базовій модуляції зміщенням

Вплив напруги колекторного живлення Е_к. Залежності струмів і напруги від напруги живлення називаються статичними модуляційними характеристиками при колекторній модуляції. Вони приведені на мал. 1.16. Очевидно, що в даному випадку формування амплітудно-модульованих коливань можливе тільки в перенапруженому режимі.

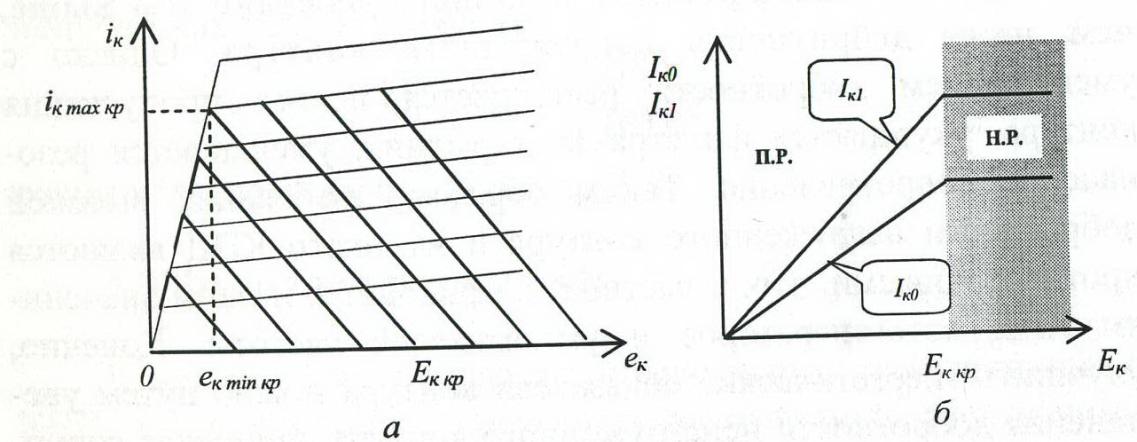
Мал. 1.16

а – зміщення динамічної характеристики при змінені колекторного живлення ; б – статистичні модулюючі характеристики при колекторній модуляції

1.7 Коефіцієнт корисної дії контура

Раніше ми відзначали, що частина корисної потужності розсіюється в контурі, остання частина передається в навантаження. Як зв’язаний коефіцієнт корисного дії контура з його параметрами? Розглянемо еквівалентну схему контура (мал. 1.17).

Мал. 1.17 – Еквівалентна схема коливального контуру

На цьому малюнку позначено: L_к, С_к - індуктивність і ємкість контура, r₀ і r_вн - власне і коливального контура що вноситься опори відповідно. Вихідна потужність Р_вих = 0,5І²_конт r_вн, де І_конт - амплітуда контурного струму. Повна потужність Р₁ = 0,5І²_конт (r₀+r_вн). Тоді ККД контура можна записати в наступному вигляді:

η_к = Р_вих / Р₁ = r_вн / (r₀+r_вн)

Після невеликих і достатньо простих перетворень цю формулу можна привести до наступного вигляду:

η_к = 1-Q_н / Q_xx

де Q_н - добротність навантаженого контура, Q_хх - добротність ненавантаженого контура (холостий хід).

Видно, що коефіцієнт корисної дії тим вище, чим нижче добротність навантаженого контура. Проте із зменшенням добротності розширюється смуга пропускання контура, погіршується фільтрація гармонік, зменшується резонансний опір. Таким чином, вимоги високої добротності навантаженого контура і високого ККД є суперечливими, що, зокрема, приводить до низьких значень ККД автогенераторів і помножувачів частоти. Звичайно, поліпшити енергетичні показники контура можна шляхом збільшення добротності ненавантаженого контура, зменшуючи опір власних втрат або збільшуючи характеристичний опір.