3. Вычисление функции Бесселя

Как видно из формулы (1.7), в ходе вычисления коэффициента волнового сопротивления требуется вычисление функции Бесселя (I_3/2(z)), а точнее ее квадрата.

Как известно:

(3.1)

Введем функцию:

(3.2)

(3.3)

График функции I^*(z) приведен на рис.4. Свойства этой функции аналогичны свойствам функции I_3/2(z). Так при z функция I^*(z)0 и функция I_3/2(z)0. При z0 функция I^*(z)0.

Рассмотрим асимптотическое поведение I^*(z) при z0. Ограничимся двумя членами при разложении в ряд Маклорена.

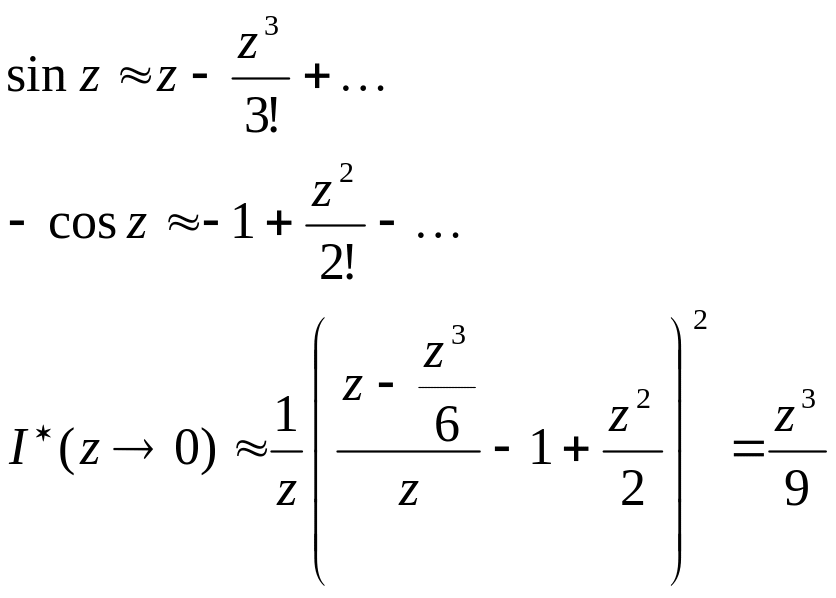
Таким образом I^*(z) вблизи точки z = 0 эквивалентна , то есть:

(3.4)

С учетом (3.2) сила волнового сопротивления запишется так:

(3.5)

I^*(z)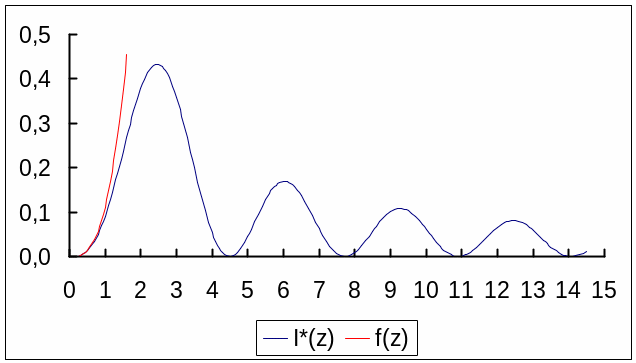

Рис. 4

4. Получение расчетных формул для коэффициента волнового сопротивления

1. Основные посылки при получении формулы для коэффициента волнового сопротивления

1. Объем эллипсоида при изменении его геометрических характеристик остается неизменным, то есть:

, (4.1)

где r – радиус эллипсоида, с осью вращения направленной по оси Ox

при той же длине эллипсоида и постоянной объеме;

2. задаются соотношения плотностей жидкостей , и вектор скорости, направленный вдоль оси Ох.

3. Число Фруда вычисляется по двум полуосям в направлении скорости, то есть по :

Тогда (4.2)

4. Все вычисления проводятся в безразмерном виде, считаются безразмерные характеристики потока и соотношения геометрических параметров эллипсоида

5. Задается расстояние от границы раздела до центра эллипсоида в безразмерном виде – . Необходимо также обеспечить условие непересекания эллипсоидом границы раздела:

(4.3)

Это условие равносильно

(4.4)

В случае невыполнения этих условий расчет волнового сопротивления требует другого подхода.

6. Коэффициент волнового сопротивления получим по общим принципам обезразмеривания

.

В качестве S_o возьмём

, тогда (4.5)

4.2 Вычисление коэффициента волнового сопротивления для эллипсоида вращения

4.2.1 Коэффициент Сх для эллипсоида вращения, с осью направленной вдоль оси Ох

В этом случае (см. также (2.3)). При этом, с учетом :

С учетом (4.2) получаем, что .

С учетом (4.1) получаем, что ; .

Учитывая все это, из (3.5) получаем формулу волнового сопротивления, для тела, движущегося под свободной поверхностью:

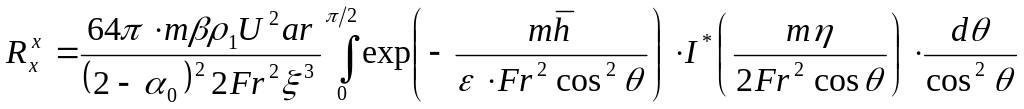(4.6)

(4.7)

Условие не выхода на поверхность при принимает вид .

_о определяется из (2.4) или (2.5) в зависимости от ₁.

При ("нить", параллельная потоку), ₁, 1, _о0 и 0, что соответствует физике задачи.

Исследуем предельный переход: ₁1, 0 , 0, _о=2/3. При этом (вспомним (1.5)):

, тогда:

(4.8)

Покажем, что при   1 (4.7)  (4.8). При  0 можно воспользоваться асимптотическим разложением функции I^* (4.4).

Таким образом предельный переход выполнен.