Расчет волнового сопротивления эллипсоида, движущегося вблизи границы раздела сред различной плотности Содержание

Введение. Постановка задачи _____________________________________стр. 2

Вычисление волнового сопротивления _____________________________стр. 3

Определение _о ________________________________________________стр. 5

О вычислении функции Бесселя ___________________________________стр. 11

Получение расчетных формул для

коэффициента волнового сопротивления ___________________________стр. 13

Алгоритм. Особенности и методика

расчета на ЭВМ. Описание программы ____________________________стр. 18

Введение. Постановка задачи

Рассмотрим линейную пространственную задачу о волновых движеениях, возникающих вблизи границы раздела двух идеальных жидкостей с плотностями ₁ и ₂ при равномерном, прямолинейном, горизонтальном премещении твердого тела в жидкости с плотностью ₁.

Н.Е. Кочиным в [1] предложено общее решение такой задачи для тела произвольной формы, движущегося под свободной поверхностью. В данной работе приведено решение и расчет для тел простейшей формы – сферы и эллипсоида.

Волны. Образующиеся на границе раздела при движении тела на постоянной глубине h с постоянной скоростью U в жидкости с плотностью ₁, будем считать малыми, а поверхность тела достаточно гладкой.

U

₁

₂

Более подробно постановка задачи, граничные условия и введенные допущения приведены в [1] и [2]. Перейдем непосредственно к вычислению волнового сопротивления.

₂

₁

h

h

U

а) б)

Рис. 1 К постановке задачи

а)

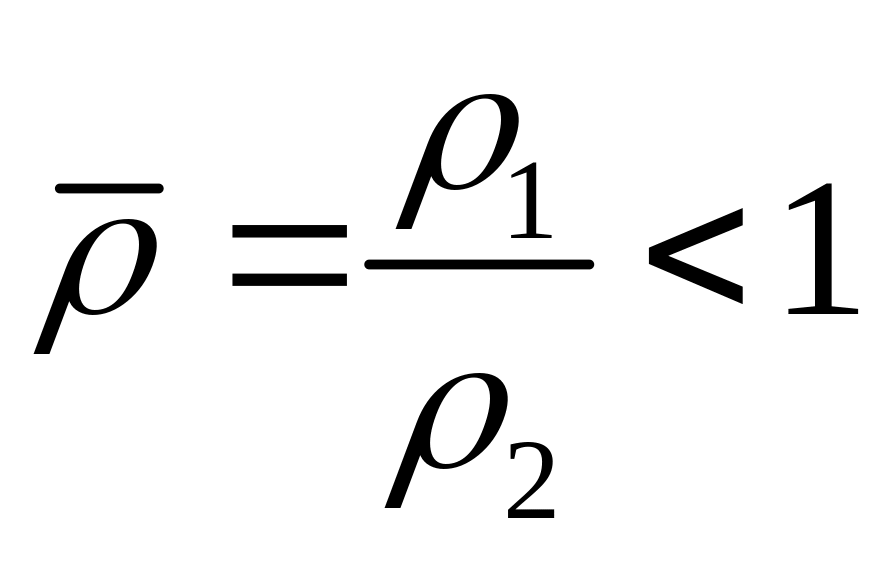
б)

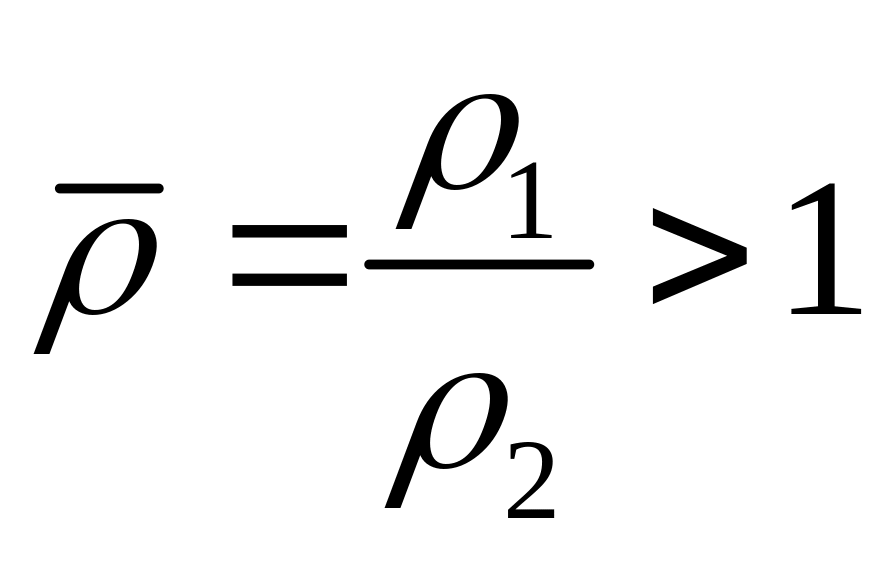
1. Вычисление волнового сопротивления

Подробный вывод выражения для волнового сопротивления в общем случае содержится, например, в [1]. Там же можно найти и выражение для функции, введённой Н.Е. Кочиным, которая в дальнейшем будет именоваться функцией Кочина.

Проекция суммарной гидродинамической силы на направление движения тела, совпадающего с горизонтальной осью Ох, - R_x, названная силой волнового сопротивления. Кочиным Н.Е. была предложена формула для силы волнового сопротивления, которая справедлива для тела, движущегося под свободной поверхностью:

, (1.1)

где _о – плотность жидкости, - функция Кочина,

, (1.2)

g = 9,81 м/с² – ускорение свободного падения, U – скорость движения тела.

В случае движения тела вблизи границы раздела, смотри [5], эта формула запишется так:

, (1.3)

где , ₁ - плотность жидкости, в которой находится тело,

, (1.4)

При движении тела под свободной поверхностью, то есть при   (строго говоря,   800) к_о =  и формула (1.3) становится тождественна (1.1). Существенно упростить вычисление функции Кочина можно, если представить потенциал относительного движения в виде:

,

где f(q) – функция координат, принимающих на поверхности тела постоянное значение, этому условию соответствуют сфера и эллипсоид.

Выражение для R_x сферы радиуса r_o, движущейся со скоростью U, принимает слудующий вид:

, (1.5)

где . (1.6)

В случае эллипсоида R_x может быть вычислено по формуле:

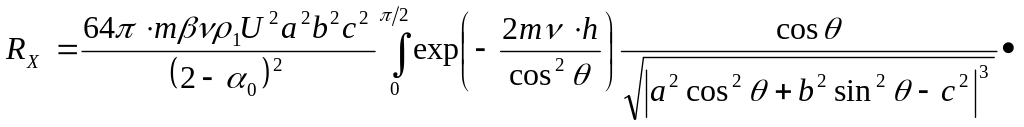
, (1.7)

где a, b, c –полуоси эллипсоида в направлении x, y, z соответственно, причем:

,

I_3/2(z) – функция Бесселя, _о – величина, определяемая интегралом:

, (1.8)

где u – координата, в выбранной системе координат.

Свойства _о будут рассмотрены ниже.

Полученные формулы позволяют получить R_x сферы и эллипсоида при допущениях линейной теории.

В дальнейшем для сокращения аналитических выкладок будет рассматриваться случай движения под свободной поверхностью, но на стадии расчета вернемся к границе раздела.