
- •Лекция № 16.
- •Содержание
- •Системы счисления.
- •Двоичная арифметика.
- •Основные аксиомы и законы булевой алгебры.
- •Набор логических функций двух переменных
- •Минтермы, макстермы и значения функции у10
- •Основные аксиомы и законы булевой алгебры
- •Выполнение логических и арифметических операций.
- •Принципы схемотехники цифровых интегральных схем.
Лекция № 16.
Основы булевой алгебры.
Содержание
1. Системы счисления. 1
2. Двоичная арифметика. 4
3. Основные аксиомы и законы булевой алгебры. 7
4. Выполнение логических и арифметических операций. 11
Принципы схемотехники цифровых интегральных схем. 14
Рассмотрим первый вопрос лекции.
Системы счисления.
Всякое число представляется (кодируется) набором цифр в определенной системе счисления. Наибольшее распространение получили позиционные системы счисления, в которых каждая цифра выражает число не только своим значением, но и положением (позицией) среди других цифр. Основание системы − это число q, равное количеству разных цифр, необходимых для выражения всех чисел в пределах одного разряда. Положительное число из i разрядов в позиционной системе с основанием q может быть представлено как
![]() (10.1)
(10.1)
где а – любая цифра от 0 до q – 1 включительно;
первый член представляет собой старший разряд числа, а последний − младший.
Кодированное в десятичной системе счисления число, например, 397, представляется как 39710 = 3∙102 + 9∙101 + 7∙10о.
В цифровой технике нашли преимущественное применение элементы с двумя рабочими состояниями, одно из которых отождествляется с цифрой 1, а второе – с 0. Поэтому здесь распространено так называемое натуральное двоичное кодирование, при котором n- разрядное число выражается как
![]() (10.2)
(10.2)
где
![]() может принимать значение 1
или 0. Например,
число 1310
при двоичном кодировании имеет вид
11012.
может принимать значение 1
или 0. Например,
число 1310
при двоичном кодировании имеет вид
11012.
Наряду с этим находят применение и другие коды, позволяющие упростить арифметические действия. К ним относятся, в частности, обратный и дополнительный коды.
Двоичное число в обратном коде является инверсией прямого кода (все нули прямого кода числа заменяются единицами, а единицы – нулями). Дополнительный код образуется из обратного кода добавлением к нему 1. Так, десятичному числу 13 в обратном двоичном коде соответствует число 0010, а в дополнительном − 0011.
В таблице 1 приведены примеры записи чисел в двоичной, десятеричной и шестнадцатеричной системах счисления.
Таблица 1.
2 |
10 |
16 |
0000 |
0 |
0 |
0001 |
1 |
1 |
0010 |
2 |
2 |
0011 |
3 |
3 |
0100 |
4 |
4 |
0101 |
5 |
5 |
0110 |
6 |
6 |
0111 |
7 |
7 |
1000 |
8 |
8 |
1001 |
9 |
9 |
1010 |
10 |
A |
1011 |
11 |
B |
1100 |
12 |
C |
1101 |
13 |
D |
1110 |
14 |
E |
1111 |
15 |
F |
Как видно из таблицы, в двоичной системе счисления каждое последующее число получается прибавлением единицы к младшему разряду, причем сумма нуля и единицы дает единицу, а сумма двух единиц дает нуль и перенос единицы в старший разряд, где снова суммируется цифра разряда и перенесенная единица и т.д. Такая операция называется сумма по модулю два.
Широко применяется двоично-десятичный код, в котором цифры каждого разряда десятичного числа представляются четырехразрядным двоичным числом (тетрадой). Так, число А10 = 397 в двоично-десятичном коде имеет вид А2 − 10 = 0011 1001 0111. Основное достоинство двоично-десятичного кода заключается в простоте взаимного перевода десятичных и двоичных чисел аппаратными средствами. Главный недостаток – громоздкость записи и избыточность, так как шесть двоичных комбинаций в каждой тетраде (от 10102 = 1010 до 11112 = 1510) не используются.
Последнего недостатка лишено двоично-шестнадцатеричное кодирование. Здесь все 16 двоичных комбинаций тетрад используются. Они соответствуют числам в шестнадцатеричной системе счисления, обозначаемым от 0 до 9 десятичными цифрами и от 10 до 15 буквами А, B, C, D, Е, F. Например, число 39710 в шестнадцатеричном коде имеет вид 18D16 (1∙162 + 8∙161 + 13∙16о), а в двоично-шестнадцатеричном – 0001 1000 11012 − 16. Как видно, здесь тетрады отображают числа 1, 8 и D шестнадцатеричной системы счисления, а в совокупности представляют собой обычный двоичный код.
Перевод чисел из системы счисления с произвольным основанием q в десятичную систему счисления (q=10) выполняется по вышеприведенным формулам, для чего требуется перевести в десятичную систему счисления числа аi и q. Несколько сложнее перевести числа из десятичной системы счисления в систему счисления с основанием q10. Наиболее просто такая операция выполняется для q=2, 8, 16.
Пусть требуется перевести число (1993) в шестнадцатеричную систему счисления. Перевод осуществляется последовательным делением десятичного числа на основание системы счисления q = 16.
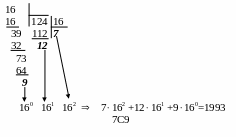
Перевод из десятеричной в двоичную систему счисления осуществляется последовательным делением десятичного числа на основание системы счисления q=2.
13 2 12
6 2 1
6 3 2 0
2 1
1
20
21
22
23
123
+122
+021
+120=13
1101









Перейдем ко второму вопросу лекции.
