4. Алгебраїчні криві 2-го порядку.

О. Еліпсом наз. ГМТ, сума відстаней від кожної з яких до двох фіксованих точок площини (фокусів) є величина стала, і більша ніж відстань між фокусами.

О. Гіперболою наз. ГМТ, різниця відстаней від кожної з яких до двох заданих точок є величина стала, вказана різниця береться по модулю і менша відстані між фокусами, але відмінна від нуля.

О. ГМТ, рівновіддалених від заданої точки (фокуса) і фіксованої прямої (директриси), що не проходять через фокус наз. параболою.

Розглянемо еліпс.

, за озн. .

— фокальні радіуси

, , , отримаємо: (*), де , т. М рівновіддалена від і задовільняє р-ня (*) і навпаки.

Отже, (*) — р-ня еліпса, числа — півосі еліпса, — велика, — мала.

О. Ексцентриситетом еліпса наз. відношення відстані між фокусами до довжини його великої осі. . . встановлює зв’язок між великою і малою осями, а отже характеризує й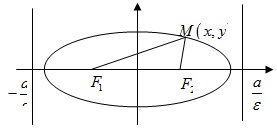 ого форму.

Раціональні вирази фокусних радіусів.

, , , . , , , .

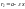Директриси еліпса

О. Дві прямі, до великої осі еліпса і розташовані симетрично відносно центра на відстані від нього наз. директрисами еліпса.

Я кщо — відстань від дов. т. еліпса до його фокуса, — вівдстань від тієї ж т. до відповідної директриси, то . ( , )

Дослідження ф-ли еліпса

;

Р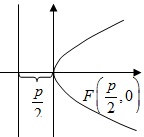 озглянемо І чверть

ф-ція спадна

Гіпербола ,

асимптоти: . — ексцентриситет

- дотична

Парабола: — канонічне рівняння — рівняння дотичної.

5.Теорія площин у просторі (аналітичний виклад).

Нехай в просторі задана загальна система координат x, y, z – змінних.

О. Рівнянням від трьох змінних x, y, z наз. рівняння f(x, y, z)=0. F(x, y, z)=0- деякий аналітичний вираз, що одночасно не перетворюється в 0 при всіх значеннях змінних x, y, z . Якщо ж рівність (1) f(x, y, z)=0 справджується при всіх змінних, то в она наз. тотожністю.

О . Поверхнею наз. ГМТ простору, координати яких в деякій системі координат задов. рівняння (1). Найпростіші із поверхонь є площини. Розглянемо можливі задання площин.

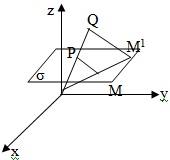
а ) Нехай задано т. і два не колінеарні вектори а і b ║δ, тоді т. і визначають площину в просторі. Нехай точка М має такі координати , , . В такому разі трьома числами характеризується площина в просторі. Точка М – початкова точка площини, а і b – напрямні вектори.

б) Нехай δ задана трьома точками , , . Площина задана дев’ятьма числами.

в) Площина може задаватись також трьома точками, розташованими в системі координат .

Т. В загальній декартові системі координат площину записують рівнянням першого степеня, виду ax+by+cz+d=0.

Д ов.: Зафіксуємо на площині σ довільну точку та виберемо на ній два не колінеарні вектори і . , , . Нехай довільна точка М площини σ має координати . , , - ці вектори є компланарними. Маємо визначник: =0 (2) , Покажемо, що А=В=С≠0. Ці числа будуть пропорційні, а це неможливо.

Т. Довільне рівняння першого степеня в загальній Декартові системі координат задає рівняння площини.

Часткові випадки розташування площин.

Д=0 - площина проходить через точку О(0;0).

С=0. Тоді нормальний вектор n(А,В,0) він перпендикулярний до OZ. Площина σ ║OZ.

В=0 σ ║OY. 4)А=0 σ ║ОХ. 5) Д=С=0 площина проходить через вісь OZ. 6) Д=В=0 σ ║ZOY. 8) А=В=0 σ ║ХOY. 9) В=С=Д=0 σ ║YОZ. 10) A=C=D=0 σ =ХOZ. 11) А=В=С=0 – це неможливо.

Рівняння площини, що проходить через три точки.

Н 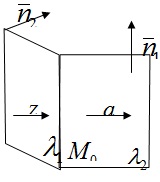ехай в просторі площина визначається трьома точками , . Точка М - біжуча точка. . Аналогічно і . Маємо визначник: (1) – Рівняння площини, що проходить через три точки.

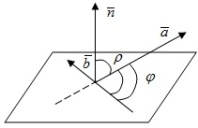
Параметричне рівняння площини.

Нехай площина σ задана т. і двома векторами , , . Тоді будуть компланарні. Оскільки а непаралельне b, можна подати через два не компланарні вектори .

- параметричне рівняння площини.

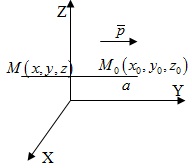
Нормальне рівняння площини .

Зведення загального рівняння площини до загального.

,

,

. Знак не повинен бути протилежним до вільного члена р.

О. Відхиленням т. від площини σ назив. додатнє число δ=d, якщо т. ­ і початок координат розміщені по різні боки від площини і δ=-d, якщо по один бік.

Т. Відхилення т. від площини σ = лівій частині нормального рівняння площини, де замість біжучих координат підставляють координати т. , .

Взаємне розташування площин

Т. Система лінійних рівнянь сумісна тоді і тільки тоді, коли ранг розташованої матриці системи дорівняє рангу основної матриці.

О. Пучком площин назив. сукупність тих і тільки тих площин простору, що проходять через одну пряму – вісь пучка.

Т. Якщо в площині декартової системи координат задані дві площини і загальними рівняннями і ці площини перетинаються по прямій l, то .

О. В’язкою площин наз. сукупність тих і тільки тих площин простору, що проходять через одну і ту ж точку, яка наз. центром в’язки.