2.2. Реставрация изображений
Реставрацией называют процесс компенсации
искажений наблюдаемого изображения
с целью получения оценки
некоего идеального изображения
,
которое наблюдалось бы на выходе
идеального датчика, не вносящего никаких
искажений. Искажения могут вноситься
турбулентностью атмосферы, расфокусировкой
оптики, недостаточным временем
экспозиции, смещением датчика в процессе
формирования изображения (размытость
контуров наблюдаемых объектов) и т.п.
Очевидно, что эффективность реставрации
зависит от адекватности используемых
моделей пространственных искажений.
В литературе, посвященной цифровой
обработке изображений, описание
рассматриваемых ниже методов реставрации
приводится для непрерывных изображений
и
,
хотя в действительности наблюдаемое
изображение и получаемая оценка
идеального изображения являются
дискретными (
и
соответственно).
Пусть математическая модель искажений
имеет вид двумерного линейного фильтра
с импульсной характеристикой
.
Тогда частотная характеристика
искажающего фильтра определяется как
двумерное преобразование Фурье его
импульсной характеристики
, (7)
где
.
Если идеальное изображение рассматривается
как реализация двумерного случайного
процесса с нулевым средним и известным
энергетическим спектром
,
а к искаженному изображению добавляется
аддитивный гауссовский шум с нулевым
средним и известным энергетическим
спектром
,
то минимальная среднеквадратическая
ошибка реставрации достигается
использованием винеровского фильтра,
частотная характеристика которого
имеет вид
, (8)
где * – знак комплексного сопряжения.
Оценка идеального изображения будет определяться как обратное двумерное преобразование Фурье произведения спектра наблюдаемого изображения и частотной характеристики реставрирующего фильтра, задаваемого выражением (8):
. (9)
Если идеальное изображение не обладает
пространственной корреляцией и его
энергетический спектр принимает
единичное значение во всем диапазоне
пространственных частот
и
,
то выражение (8) приобретает более
простой вид:
. (10)
При отсутствии аддитивного шума винеровский фильтр вырождается в так называемый инверсный фильтр, имеющий частотную характеристику
. (11)
В MATLAB Image Processing Toolbox реставрация изображений с помощью винеровского фильтра реализована в виде функции deconvwnr, интерфейс которой имеет вид
=
deconvwnr(I, PSF, NCORR, ICORR),
где
– оценка идеального изображения
;
– наблюдаемое изображение
;
PSF
– импульсная характеристика искажающей
системы
,
называемая также функцией рассеяния
точки (point-spread
function); NCORR
– автокорреляционная функция аддитивного
шума (обратное преобразование Фурье
энергетического спектра
);
ICORR
– автокорреляционная функция идеального
изображения.
Автокорреляционная функция идеального изображения может быть вычислена как
ICORR = fftshift(real(ifftn(abs(fftn(J.^2))),
где fftshift(…) – перегруппировка элементов матрицы спектральных коэффициентов, полученных в результате n-мерного преобразования Фурье таким образом, чтобы низкочастотные компоненты спектра занимали центральную часть матрицы; real(…) – вычисление действительной части комплексного числа; ifftn(…) – обратное n-мерное преобразование Фурье; abs(…) – вычисление абсолютной величины действительного или комплексного числа; fftn(…) – прямое n-мерное преобразование Фурье; .^2 – операция поэлементного возведения в квадрат всех элементов массива.
Автокорреляционная функция аддитивного шума вычисляется аналогично.
Параметры NCORR и ICORR являются необязательными. Если они не указаны, то функция deconvwnr реализует инверсный фильтр, определяемый выражением (11).
Импульсные характеристики фильтров, моделирующих основные типы пространственных искажений, задаются в системе MATLAB с помощью функции fspecial. В зависимости от используемой модели искажений вызов функции может иметь следующий вид:
1) размытие контуров изображения за счет смещения камеры в процессе формирования изображения
h = fspecial('motion', len, theta),
где h – импульсная характеристика фильтра; len – величина смещения в пикселях; theta – направление смещения в градусах, отсчитываемое относительно горизонтальной оси против часовой стрелки;
2) снижение резкости изображения путем усреднения значений яркости каждой точки по окрестности, имеющей форму диска
h = fspecial('disk', radius),
где radius – радиус диска (по умолчанию – 5 пикселей); формируемая матрица h имеет размеры [2*radius+1 2*radius+1];
3) снижение резкости изображения путем свертки с дискретной аппроксимацией двумерной гауссоиды, вычисляемой по формуле
h = fspecial('gaussian', hsize, sigma),
где hsize
– размеры формируемой матрицы h
(по умолчанию – [3 3]);
sigma
– среднеквадратическое отклонение
(по умолчанию – 0.5).
Для случаев, когда априорная информация о свойствах пространственных искажений и статистических характеристиках изображения и шума недоступна, были разработаны методы слепой реставрации. В MATLAB Image Processing Toolbox для слепой реставрации изображений используется функция deconvblind, позволяющая получить итеративное уточнение оценки идеального изображения и грубой оценки функции рассеяния точки. Функция может быть вызвана следующим образом:
[J,PSF] = deconvblind(I,INITPSF),
где J – оценка идеального изображения ; PSF – оценка функции рассеяния точки; I – наблюдаемое изображение ; INITPSF – грубая оценка функции рассеяния точки.
Пример реставрации изображения описанными ранее методами с помощью функций, входящих в Image Processing Toolbox, приведен на рис. 2.
|
|
а |
б |
|
|
в |
г |
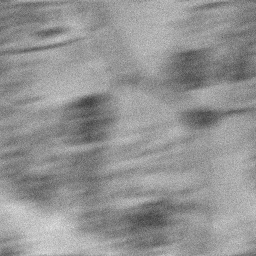
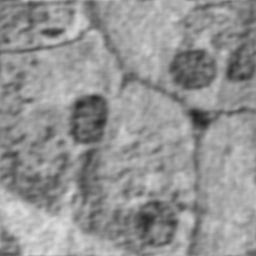
Рис. 2. Реставрация изображения различными методами: а - искаженное изображение биологических клеток живой ткани; б - оценка идеального изображения (инверсный фильтр); в - оценка идеального изображения (винеровский фильтр); г - оценка идеального изображения (слепая реставрация) |
|
В качестве наблюдаемого изображения выбрано изображение биологических клеток живой ткани (см. рис. 1, а), искаженное фильтром типа ‘motion’ с параметрами len=31 и theta=11, к которому добавлен аддитивный гауссовский шум с дисперсией 0.002. При вычислении оценки идеального изображения методом слепой реставрации в качестве грубой оценки функции рассеяния использовалась матрица такого же размера, как и реальная функция рассеяния точки, состоящая из единиц. В MATLAB такую матрицу можно задать выражением
INITPSF = ones(size(PSF)).