Диаграммы и правила их построения
Диаграммы - полезное, удобное и гибкое средство для отображения информации. Они делают возможным изображение количественных показателей в простом, ясном и наглядном виде, облегчают сравнение различных величин, выявляют тенденции их движения и взаимных связей.
Происхождение диаграмм и разработка техники их составления в нашем современном понимании восходят к 1786 г., когда У. Плейфэйр опубликовал свой знаменитый труд под названием «Коммерческий и политический атлас». Говоря о «своей линейной (графической) арифметике», У. Плейфэйр поясняет, что ему удалось предложить и ввести в практику новый и полезный способ составления отчетов. Этот способ получил всеобщее признание, поскольку благодаря ему в течение пяти минут может быть получена такая информация, которая требовала бы целых дней упорных занятий с таблицами цифр, чтобы запечатлеться в памяти.
Диаграммы как форма представления информации имеют перед другими графическими формами целый ряд преимуществ. Они дают возможность наглядно воспринимать зависимости разного рода явлений и связанные с ними процессы. Позволяют (путем экстраполяции) в достаточной степени точно прогнозировать дальнейшее протекание процессов и явлений. По направлению и крутизне наклона кривой (или прямой) удается легко предвидеть характер изменения индицируемой величины, что во многих случаях является задачей исключительной важности, например, когда в контролируемом процессе имеются какие-либо критические точки, требующие особой фиксации внимания. Другие виды зрительно воспринимаемой информации (к примеру, таблицы) явно уступают графикам в возможности прогнозирования динамики наблюдаемых величин.
В тезисной форме эти преимущества можно сформулировать следующим образом:
связи между величинами, зрительно воспринимаемые на диаграммах, читаются более ясно и запоминаются более легко, чем при чтении той же информации с помощью таблиц;
пользование диаграммами значительно сокращает время считывания, так как основные выводы из большой массы данных могут быть зрительно считаны по графику с одного взгляда;
диаграммы и графики могут обнаруживать неявно выраженные факты и связи, и тем самым стимулировать аналитическое мышление и исследование;
хорошо построенная диаграмма в большей мере, чем другие формы графического изображения цифровых данных, способна вызвать интерес и привлечь внимание читателя.
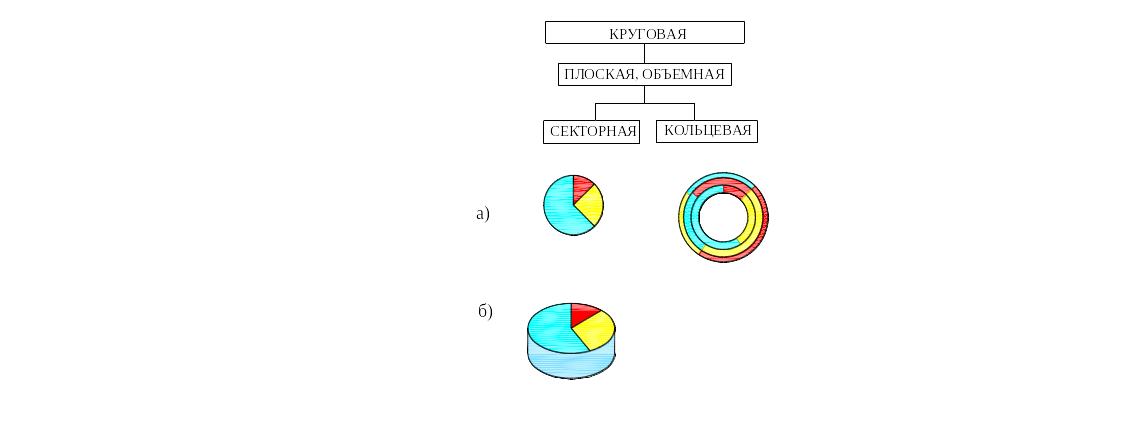
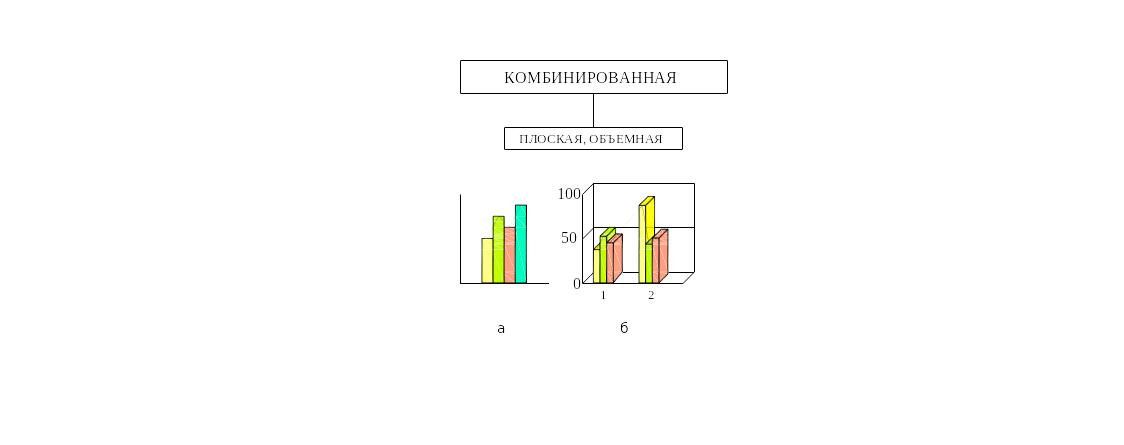
Основанием для классификации диаграмм могут служить следующие критерии: цель, условия пользования, характер сравнения, форма. Классификация диаграмм по форме представлена на рисунках 32-37.
Охарактеризуем коротко некоторые из видов диаграмм.
Объемными диаграммами называются диаграммы, выполненные с использованием аксонометрии, они особенно наглядно отражают информацию. Соотношение величин на диаграмме может быть показано при помощи линий, такие диаграммы называются линейными (рисунок 33).
Если сравниваемые величины выражены в виде различных геометрических фигур (прямоугольников, расположенных вертикально или горизонтально), то такие диаграммы называются соответственно столбиковыми (рисунок 34) или полосовыми (рисунок 35).
Диаграммы, выполненные в виде рисунков или пиктограмм, называются пиктографическими, они используются для отображения количества вещества, предметов, численности. Особый вид представляют диаграммы состояния, диаграммы состав - свойство и т. п.
Применение диаграммы той или иной формы определяется целью визуализации информации . Целью может быть отображение: функциональной зависимости; распределения величины признака объекта или явления; удельного веса составных частей целого; эмпирической (экспериментальной) зависимости параметра от фактора; сравниваемых значений признака объекта или явления; зависимости между параметрами состояния системы либо между ними и составом системы.
Рисунок 32. Классификация диаграмм по форме выполнения
Линейная диаграмма и ее основные элементы
Основной принцип построения линейных диаграмм заключается в нанесении на координатное поле отметок одного или нескольких рядов цифр в виде соответственно расположенных точек. Соединение этих точек отрезками прямой и дает линейную диаграмму. Такие диаграммы, по сути, являются графиками. Отличие линейной диаграммы от графика в том, что диаграмма более автономна по отношению к тексту, поэтому на координатном поле диаграммы может быть максимальное количество информации в виде поясняющих надписей, схем или в другой форме.
В виде линейной диаграммы (графика) может быть представлена функциональная зависимость, известная из литературы либо полученная исследователем в результате обработки данных с использованием различных методов планирования эксперимента.
Линейные диаграммы рекомендуется применять в случаях, когда более важно изобразить относительные изменения величин, а не их абсолютные значения, либо когда диаграмма предназначена для детального изучения или интерполяции.
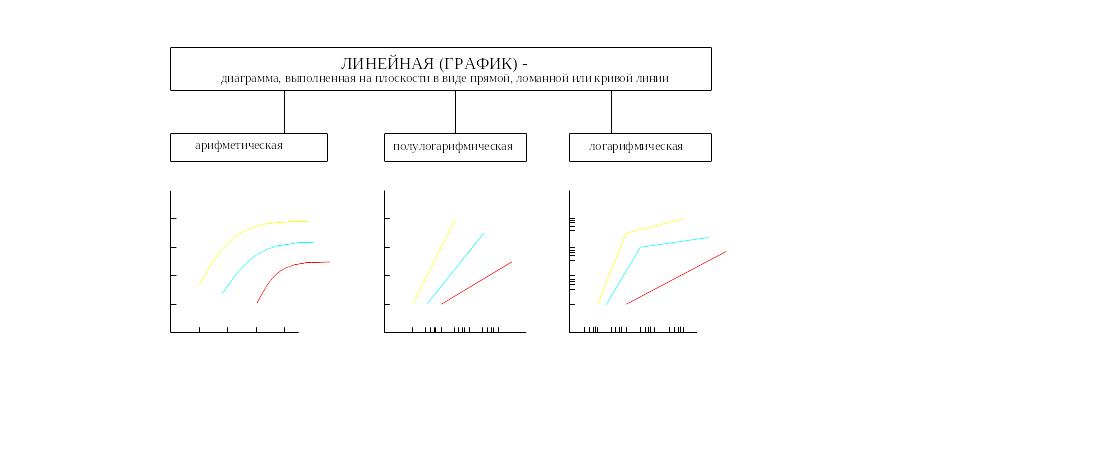
Рисунок 33. Виды линейных диаграмм
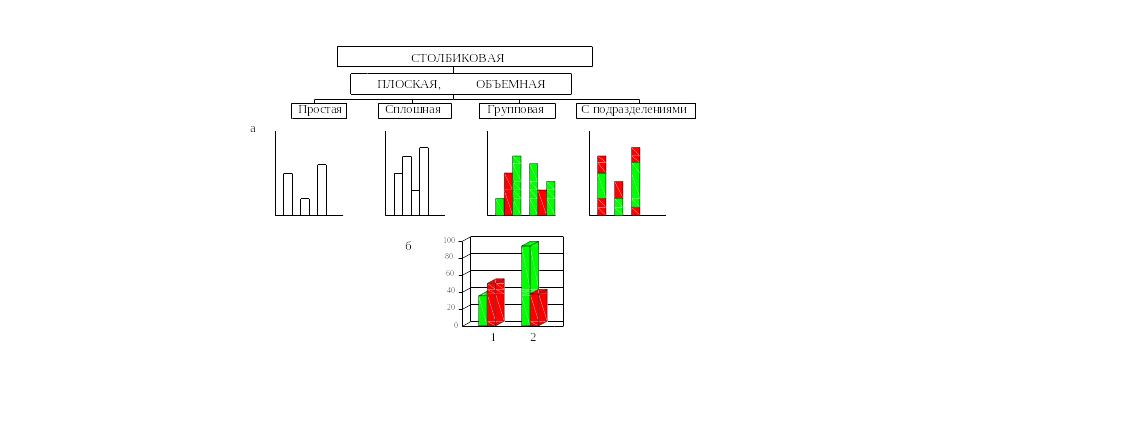
Рисунок 34. Виды столбиковых диаграмм: а - плоские; б - объемная простая
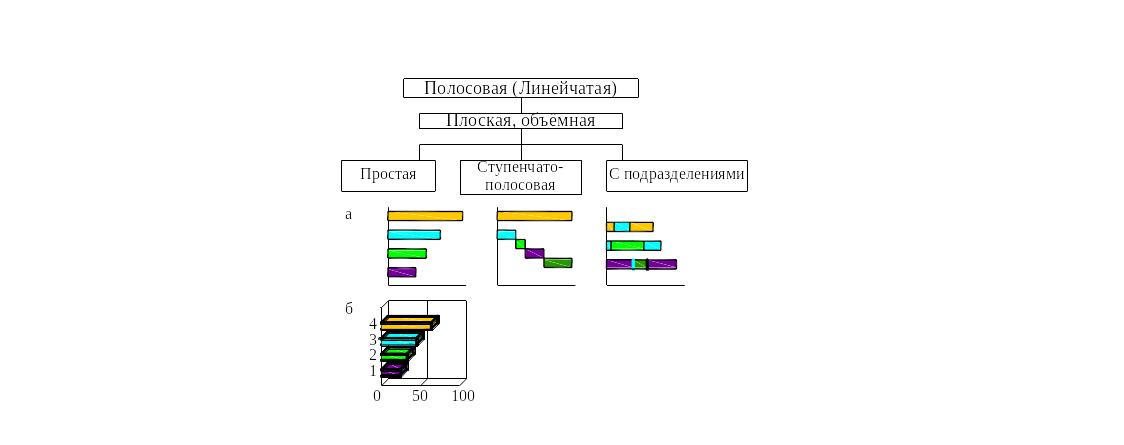
Рисунок 35. Виды полосовых диаграмм: а - плоские; б - объемная простая
|
|
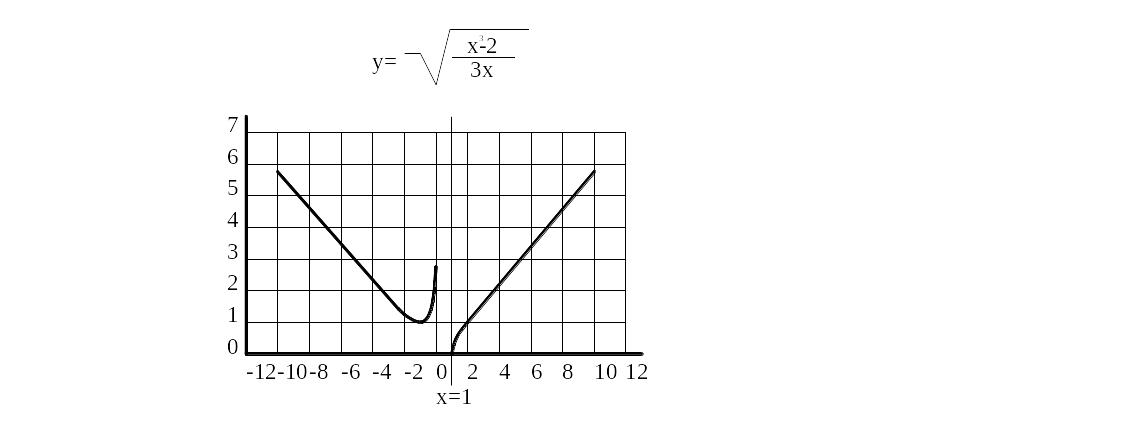
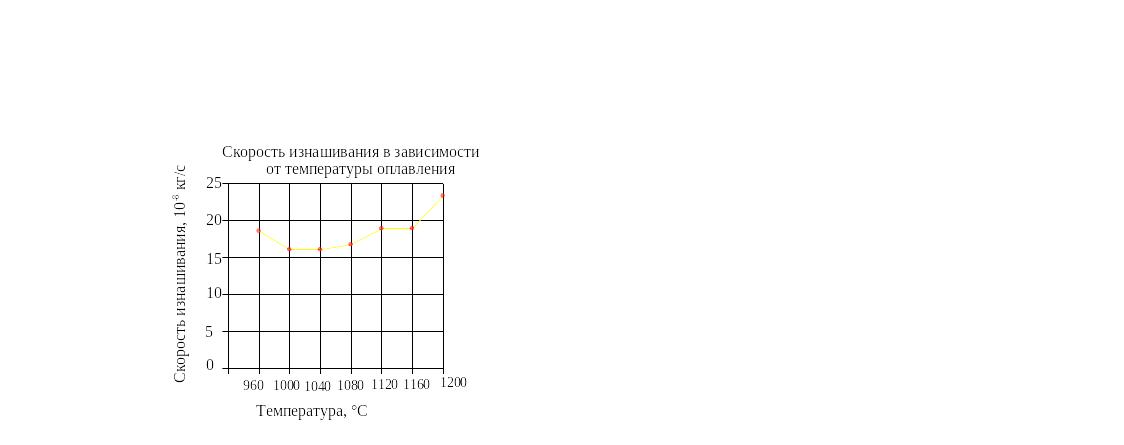
Рисунок 38. Пример линейных диаграмм
Если рассматривать линейную диаграмму как графическое средство передачи информации, то элементы диаграммы выделяются при помощи графики (типов линий и шрифтов), в зависимости от значимости передаваемой информации, в следующем порядке: название диаграммы; линии зависимостей; название линий; шкалы и их название; подзаголовки и примечания; координатная сетка.
С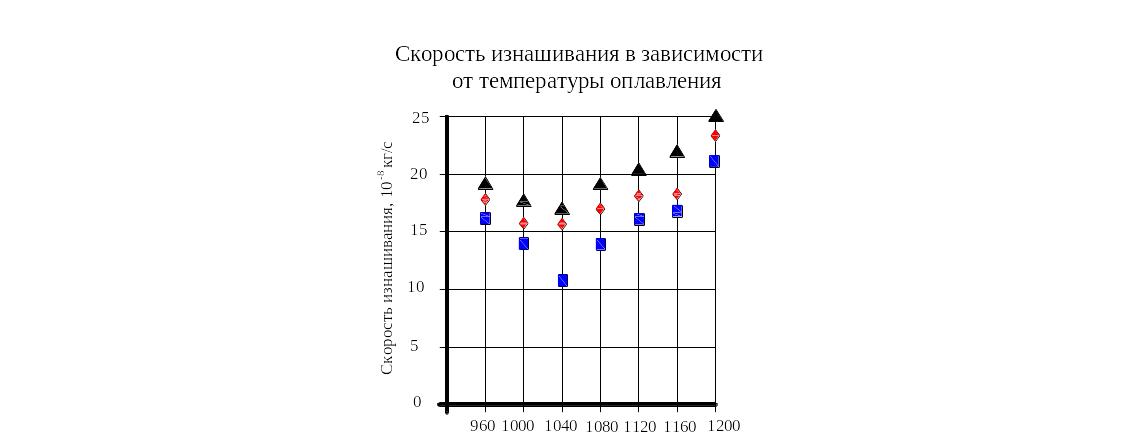
корость
изнашивания в зависимости от
температуры оплавления
Температура °С
Рисунок 39. Пример точечной диаграммы
|
|
Столбиковая диаграмма
Столбиковая диаграмма отражает влияние фактора на изменение величины параметра. На горизонтальной шкале откладывают значения фактора (независимой переменной), на вертикальной - параметра (зависимой переменной) аналогично линейным диаграммам. Главное отличие столбиковой диаграммы от линейной состоит в том, что здесь значения данных имеют дискретный характер.
Столбиковая диаграмма может демонстрировать функциональную зависимость, когда нужно подчеркнуть абсолютные значения изображаемых величин или разницу между величинами, при этом количество данных ограничено. Если же диаграмма охватывает большое количество данных, то удобнее пользоваться линейной диаграммой.
На столбиковых диаграммах данные изображаются в виде прямоугольников одинаковой ширины, расположенных вертикально. Высота каждого столбика пропорциональна изображаемым значениям величины (рисунок 40).
Диаграмма такого типа называется простой столбиковой и изображается в виде отдельных столбиков. Если значения исследуемой величины носят непрерывный характер, то для графического изображения пользуются сплошной столбиковой диаграммой, т. е. каждый столбик изображается отчетливо, но промежутков между ними не делается, такие диаграммы называются гистограммами.
Результаты исследования стойкости покрытий ПГ-СР от угла атаки
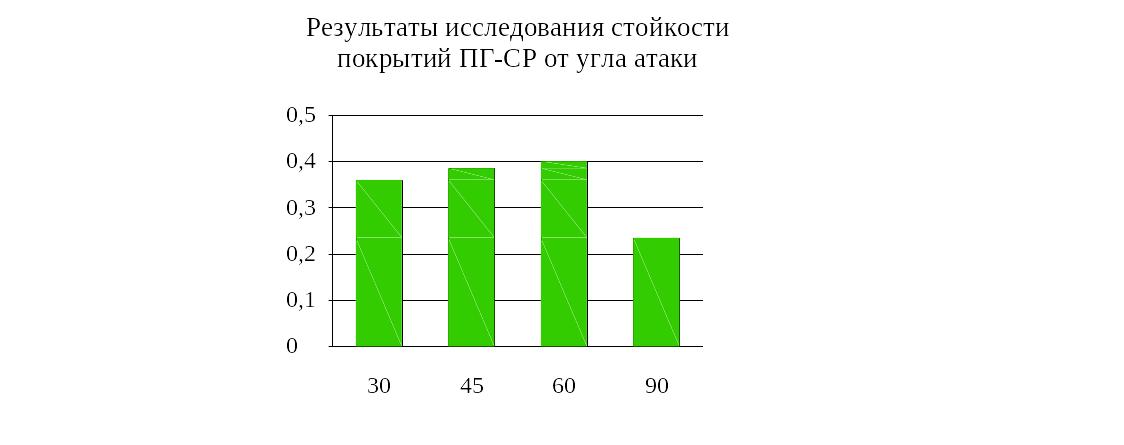
Угол атаки, град.
Рисунок 40. Простая столбиковая диаграмма
Гистограмма - диаграмма, которая графически отображает информацию о распределении величин (рисунок 41). Они используются наряду с линейными диаграммами: простыми кривыми распределения; огивами, или кумулятивными кривыми распределения; вероятностными графиками.
Распределение сферических частиц в порошке
Н70х17С4Р4
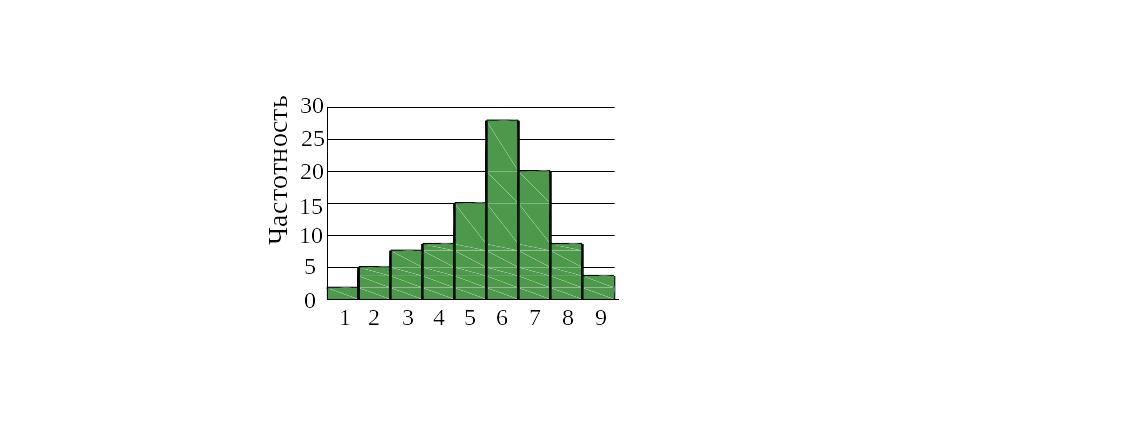
Диаметр частиц, мм
Рисунок 41. Гистограмма
Если соединить середины вершин столбцов гистограммы ломаной линией, можно получить линейную диаграмму распределения величин. Однако такая диаграмма будет нести больше информации, чем гистограмма, лишь при условии большого количества статистически обработанных данных. Для исключения некорректности представления информации о распределении величин при небольшом количестве дискретных данных или при отсутствии их статистической обработки рекомендуется использовать точечные диаграммы или гистограммы.
Простые распределения обычно изображаются на прямоугольных координатах. Вертикальная ось всегда начинается с нуля и, ни при каких условиях не прерывается. Горизонтальная шкала не должна начинаться с нуля, за исключением тех случаев, когда нуль служит низшей точкой первого группового интервала изображаемого вариационного ряда.
Типичная гистограмма строится путем возведения вертикальных линий на краях интервалов и образования ряда соприкасающихся прямоугольников, или столбиков. Площадь каждого прямоугольника представляет частоту для соответствующей группы членов ряда. Если гистограмма строится на равных интервалах, то высота каждого прямоугольника пропорциональна его площади, в этом случае высоты прямоугольников представляют частоты. Поэтому гистограммы, основанные на равных интервалах, значительно более доступны для истолкования, чем гистограммы с неодинаковыми интервалами. Иногда вертикальные линии, разделяющие отдельные столбики, опускаются, и тогда образуется ступенчатая диаграмма или ступенчатая гистограмма.
При визуализации информации используются, помимо простых, диаграммы с группами столбиков (рисунок 42). На таких диаграммах два или более столбиков из различных рядов цифр группируются вместе. При группировке они могут либо соединяться, либо разделяться узкими промежутками.
Результаты исследования стойкости покрытий от угла атаки
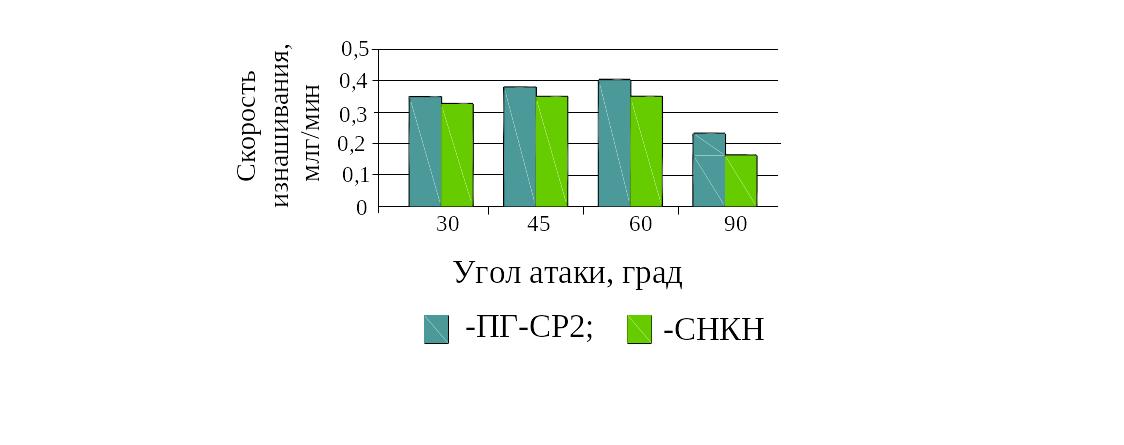
Рисунок 42. Пример диаграммы с группой столбиков
Полосовая диаграмма
Полосовые диаграммы применяются в том случае, когда факторами являются характеристики, имеющие качественный характер (условия работы и пр.). На горизонтальной оси полосовой диаграммы откладывают значения зависимого параметра, а на вертикальной - значения независимых факторов. Эти диаграммы удобны также для сравнения величин или размеров связанных между собой элементов или частей целого.
Типы полосовых диаграмм: простая полосовая (рисунок 43), полосовая с подразделениями (рисунок 44), ступенчатая полосовая (рисунок 45).
Результаты исследования стойкости покрытий
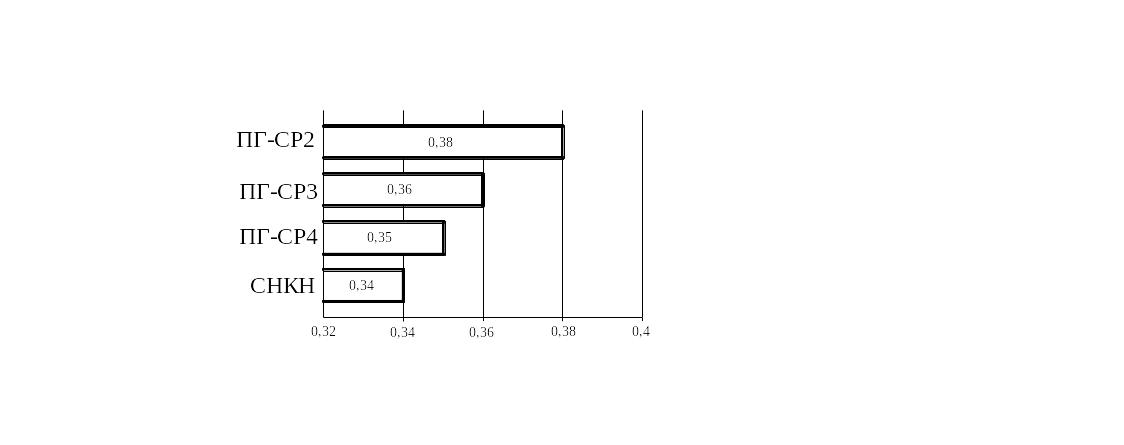
Скорость изнашивания, млг/мин
Рисунок 43. Пример простой полосовой диаграммы
Простая полосовая диаграмма употребляется для сравнения двух или нескольких сравниваемых величин. Сравнение делается на основании прямых линейных измерений. Полосы обычно располагаются в последовательности, соответствующей относительной величине показателей.
Расположение полос на простой полосовой (или линейчатой) диаграмме должно отвечать целям исследования. Обычно полосы располагают по величине, начиная с самой большой, но они могут быть расположены и в ином систематизированном порядке, если это отвечает цели составления диаграммы.
Ширина полос и расстояние между ними не имеют особого значения. Определяющим фактором при конструировании, как ширины полос, так и промежутков между ними, служит число полос, а также размер и пропорции всей диаграммы. Практически следует придерживаться правила: ширина полос на диаграмме должна быть одинаковой, а ширина промежутков - равна половине ширины самих полос. Не рекомендуется делать полосы непропорционально длинными и узкими или же короткими и широкими Важно, чтобы в каждую полосовую диаграмму включалась тщательно продуманная шкала - она и дает возможность с достаточной точностью определять длину полосы. Шкала может совпадать с верхней гранью первой полосы или же располагаться на отдельной линии в верхней части диаграммы. В этом случае промежуток между верхней полосой и линией шкалы должен быть равен половине ширины полосы.
Нулевая линия служит основной исходной точкой, и на рисунке ее следует изображать несколько толще, чем другие масштабные отметки на
шкале. Желательно, чтобы шкала не прерывалась.
Оставлять контурные полосы неокрашенными не рекомендуется. Графически полосы выполняют, применяя текстуру и цвет. Основные данные, как правило, помещаются слева от нуля, за пределами полосы.
Относительный состав материалов
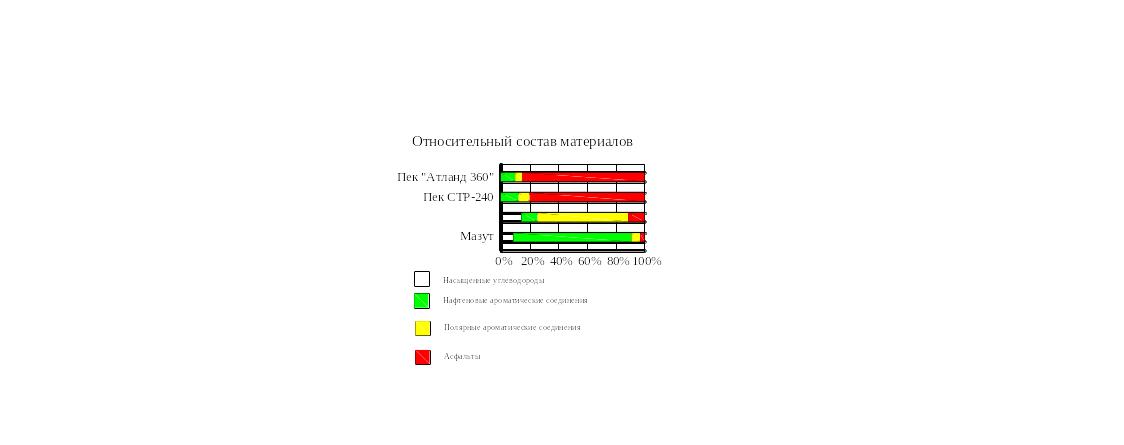
Рисунок 44. Пример полосовой диаграммы с подразделениями
Время загрузки детали в приспособление промышленными роботами
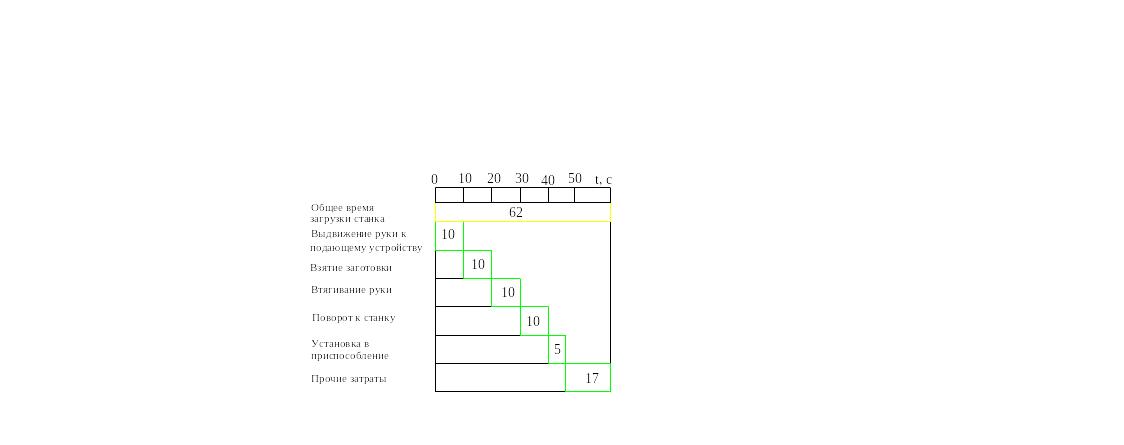
Рисунок 45. Пример ступенчатой полосовой диаграммы
Круговая диаграмма
Круговая диаграмма представляет собой круг, разделенный на секторы. Площади (или центральные углы) секторов пропорциональны изображенным значениям величин. Обычно такие диаграммы применяются для показа удельного веса составных частей целого: различные секторы круга как раз и демонстрируют составные части, или компоненты, целого (рисунок 46).
Общепринято для изображения соотношения составных частей применять одну из трех диаграмм: круговую, полосовую с процентными делениями либо простую полосовую. Каждая из этих трех графических моделей имеет свои преимущества. При выборе формы диаграммы необходимо учитывать такие факторы, как аудитория, для которой предназначается показ материала, и целевое назначение диаграммы. Более того, не существует подробных, точных, систематических и надежных тестов для сравнительной оценки различных видов диаграмм и графиков. Сравнительные оценки основаны, как правило, только на впечатлениях.
Структура затрат на производство продукции в промышленности
за 1995 г., %
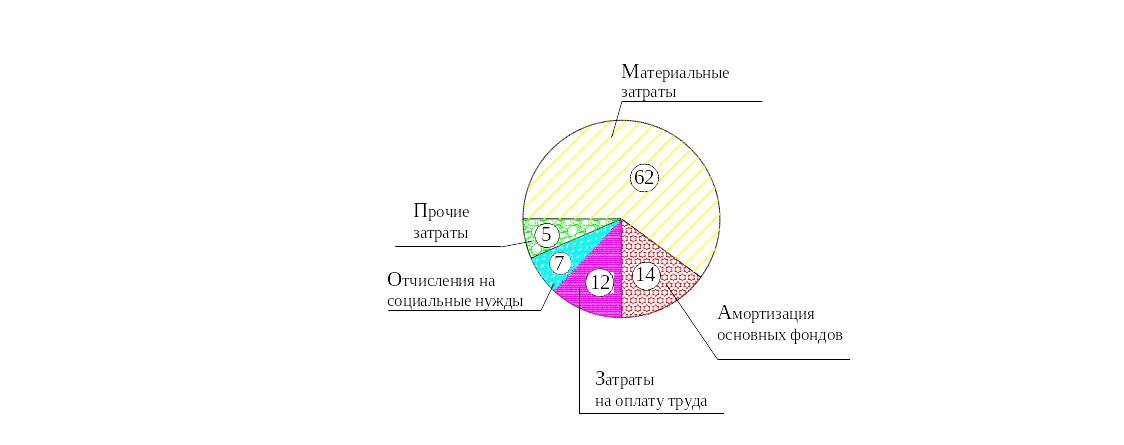
Рисунок 50. Пример круговой диаграммы
Для простых сравнений числовых данных, особенно, если имеется более четырех-пяти элементов, применяют полосовую диаграмму. При построении круговой диаграммы, прежде всего, необходимо так обработать данные, чтобы величины отдельных компонентов могли быть выражены в градусах окружности. Секторы на круговой диаграмме рекомендуется размещать в определенной логической последовательности. Чаще всего за основу берется их величина, причем самый крупный размещается сверху, а остальные - по движению часовой стрелки.
При акцентированном делении один из секторов выделяется размером, окраской или физическим отделением от целого, тем самым подчеркивается особое значение элемента.
Неопределенное деление используется для показа пределов возможного изменения делящих линий.
Сложное деление предполагает при помощи наложения секторов описывать области, принадлежащие по своему смыслу одновременно нескольким элементам. Дифференциация форм существенна, поскольку каждый из накладывающихся секторов должен четко опознаваться для передачи сложного деления.
Треугольная диаграмма применяется для одновременного изображения трех переменных, представляющих элементы, или составные части, целого. В сумме эти три величины всегда дают 100 %. Треугольная диаграмма состоит из трех шкал, построенных в виде равностороннего треугольника, каждая сторона которого разбивается на равные процентные деления от 0 до 100.
Параллельно сторонам треугольника проводят прямые линии. Треугольная диаграмма основана на геометрическом принципе, согласно которому для равностороннего треугольника сумма перпендикуляров, опущенных из любой точки прямоугольника на его стороны, есть величина постоянная и равная высоте треугольника. Ряд чисел, образующих шкалы, можно располагать последовательно как по часовой стрелке, так и против нее. Треугольная диаграмма полезна для изображения свойства химических соединений или сплавов, состоящих из трех элементов, операций, произведенных процессов (рисунок 47).
Данная диаграмма состоит из трех шкал, построенных в виде треугольника. На каждой шкале откладывается величина одного из компонентов А, В, С в %.
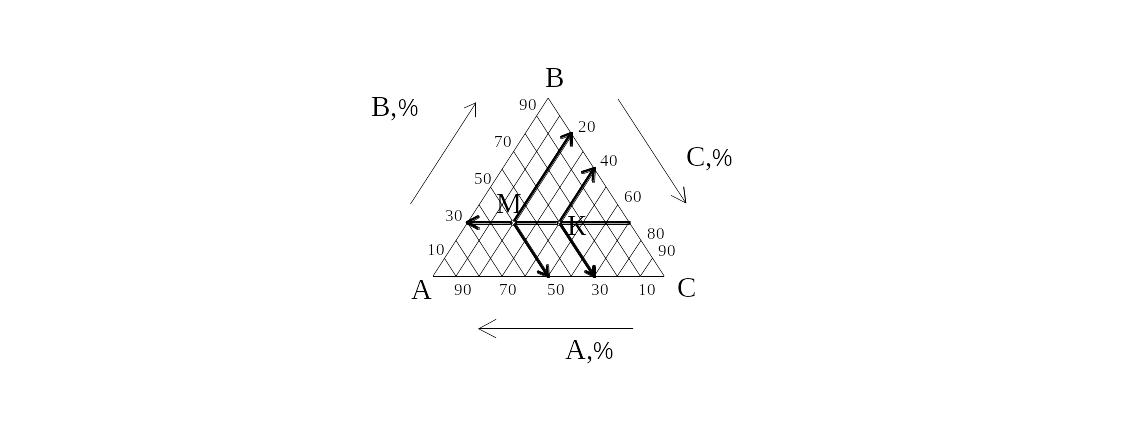
Рисунок 47. Диаграмма тройного сплава
Любая точка, лежащая внутри треугольника, соответствует составу тройного сплава. За 100 % массы удобнее всего принять длину стороны треугольника, тогда масса компонентов в тройном сплаве определится отрезками, параллельными сторонам треугольника. В вершинах треугольника лежат точки, соответствующие чистым компонентам. В данном примере в сплаве М содержится, в %: компонента А - 50, В - 30, С - 20; в сплаве К содержится: компонента А - 30, В - 30, С-40.
Треугольная диаграмма не имеет шкалы времени, но на один треугольник можно наносить три-четыре показателя за разные периоды, обозначив точки соответствующими надписями (во избежание путаницы не следует наносить слишком много цифр).
Номограммы
Номограмма - чертеж, с помощью которого можно, не производя вычислений, получать решения вычислительных задач (рисунок 48). Говоря современным языком, номограмма - это жесткая программа графического способа решения задачи. Методы и процедуры построения номограмм составляют номографию как науку. Статус самостоятельного раздела математики номография приобрела на первом Международном конгрессе математиков в 1896 г. Задачи номографии - представление физических или математических законов в графической форме, в форме номограмм.
Номограмма моделирует функциональную зависимость, и ее можно использовать как доступное и удобное вычислительное средство и как весьма наглядное и эффективное средство исследования функциональных зависимостей. Номограммы позволяют проследить влияние отдельных переменных на результат, исследовать экспериментальные особенности функции, увидеть область существования решения, обнаружить ранее неизвестные свойства функциональных зависимостей.
Номограммы - полезное дополнение к ЭВМ. Если некая задача допускает номографическое решение, точность которого достаточна, то оно оказывается более эффективным, чем машинное решение этой же задачи, состоящее в разработке стандартной программы или расчете таблицы с несколькими входами. В том же случае, когда для данной задачи точность номограмм мала, их можно применять для прикидочных расчетов, для определения нулевых приближений, для контроля вычислений с целью обнаружения грубых ошибок.
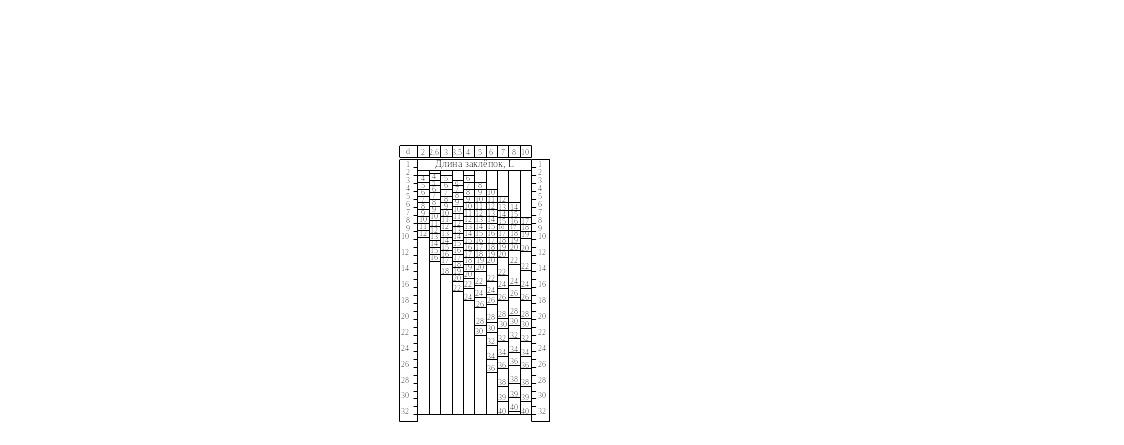
Рисунок 48. Пример номограммы с линейными
шкалами: d - диаметр заклепки; s - толщина скрепляемых деталей
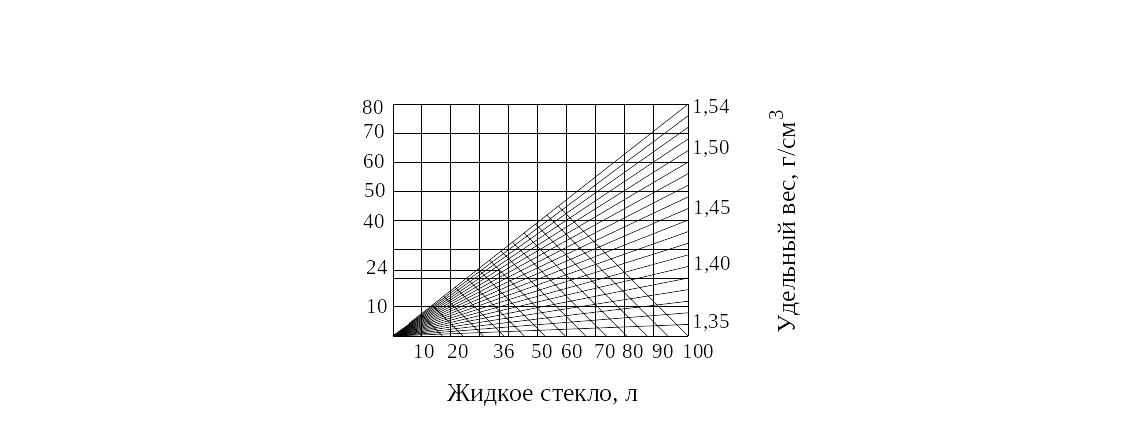
Рисунок 49. Пример номограммы сетчатой
Выгодно совместное использование номограмм и ЭВМ при решении многопараметрических задач, когда результаты расчета представляются номограммами.
Номографические методы исследования функциональных зависимостей полезно применять в задачах подбора параметров эмпирических формул по результатам наблюдений и в задачах аппроксимации одной функции другой. Номограммы позволяют охватить взглядом все множество решений данной задачи и выбрать оптимальное, компактно и наглядно изображать таблицы с несколькими входами, исследовать положенные в их основу зависимости.
Пользование готовой номограммой не вызывает трудностей (они могут возникнуть лишь при ее построении). Важные свойства номограмм: быстрота нахождения ответов, малая вероятность грубых ошибок, простота решения обратных задач. Номографический расчет не требует специальной подготовки, и для его выполнения, кроме номограмм, необходимы только карандаш и линейка.
Типы номограмм. Применяются следующие номограммы: график функции; сдвоенная шкала (рисунок 48); номограмма сетчатая (рисунок 49); из выровненных точек; циркульная; с параллельным индексом; с крестообразным индексом; барицентрическая; ромбоидальная; транспарантная. Наиболее просты и доступны в работе номограммы с прямолинейными шкалами, они используются, на пример, при расчете и выборе заклепок (см. рисунок 48).
Пояснительный текст к номограмме. В нем указываются зависимости, представленные в виде номограмм; обозначения переменных; способы пользования номограммой; примеры решения задач на номограмме; методика построения номограммы и уравнения их элементов.
МЕТОДИЧЕСКИЕ УКАЗАНИЯ К ВЫПОЛНЕНИЮ ГРАФИЧЕСКОГО ЗАДАНИЯ «ВИЗУАЛИЗАЦИЯ ИНФОРМАЦИИ О ПРОЦЕССАХ И ЯВЛЕНИЯХ»
Данные по химическому составу вещества представить в табличной форме. Таблицы выполнить с помощью текстового редактора Word. Построить диаграммы (два-три типа) с помощью программных средств AutoCAD .
Выбрать ту диаграмму(ы), которая(ые), по Вашему мнению, наиболее полно и наглядно отражает передаваемую информацию.
Обосновать выбор в текстовой форме объемом не менее 1 страницы.
Задание выполняется в виде реферата на листах белой бумаги (формат А4) с использованием программных средств: первый лист должен содержать задание в исходной форме; второй и последующие - разработанные таблицы и диаграммы с обоснованием выбора.