Задача. № 2 - расчет и построение геометрической картины нормального эвольвентного зацепления двух зубчатых колес

Исходными параметрами для решения задачи являются: передаточное число u₁₂= 1,8 , число зубьев- меньшего колеса z₁ = 17, модуль зацепления m=5мм, угол зацепления а=20°. Требуется определить основные параметры зубчатой переда­чи и построить геометрическую картину нормального эвольвентного зацепления двух зубчатых колес.

I. Определение размеров зубчатого зацепления

Произведем расчёт основных параметров зацепления.

Передаточное число зубчатой передачи может быть выражено через количество зубьев колёс

Определим число зубьев второго (большего) колеса

Полученное значение z₂ округлим до ближайшего большего, т. е. примем z₂=31.

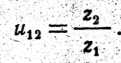
Вычислим диаметры начальных окружностей колес

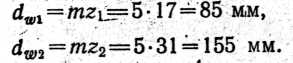
Расстояние a_w2 между осями двух колес, находящихся в зацеплении, равно сумме радиусов начальных окружностей,

Для нормального зубчатого колеса "принято, что высота головки зуба равна

а высота ножки зуба

или

Высота головки зуба h_a делается несколько меньше высо­ты ножки зуба h_f, для того чтобы вершина зуба одного коле­са не упиралась в основание впадины другого колеса.

Высота зуба h=h_a+h_f=5+6,25=11,25мм.

Определим диаметры окружностей выступов зубчатых колес

Диаметры окружностей впадин зубчатых колес равны:

Вычислим , диаметры основных окружностей зубчатых колес

Определим шаг зацепления по дуге начальной окружности

Толщина зуба S_w и ширина впадины e_w по дуге начальной окружности равны между собой, т.е.

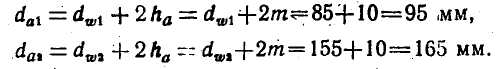
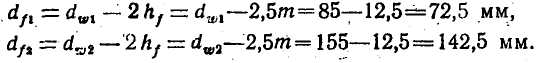
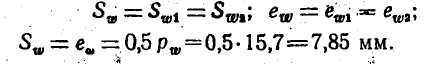
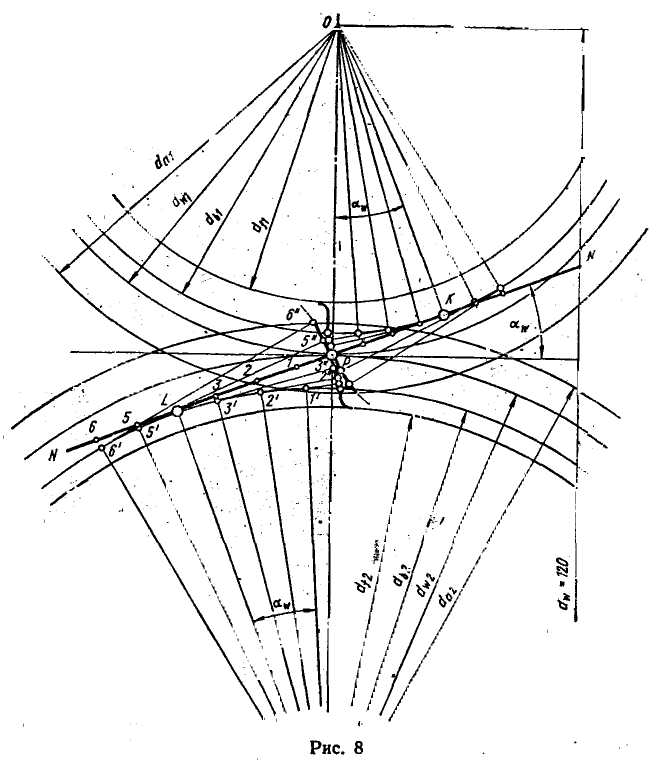
II. Построение нормального эвольвентного зубчатого зацепления

Построение зубчатого зацепления ведется в следующем порядке (рис. 8):

1. Согласно рекомендациям, данным в задании, масштабная высота зуба должна быть, не менее 30 мм, тогда

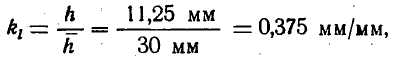
Где h— действительная высота зуба;

Вектор h— масштабное значение высоты зуба на чертеже.

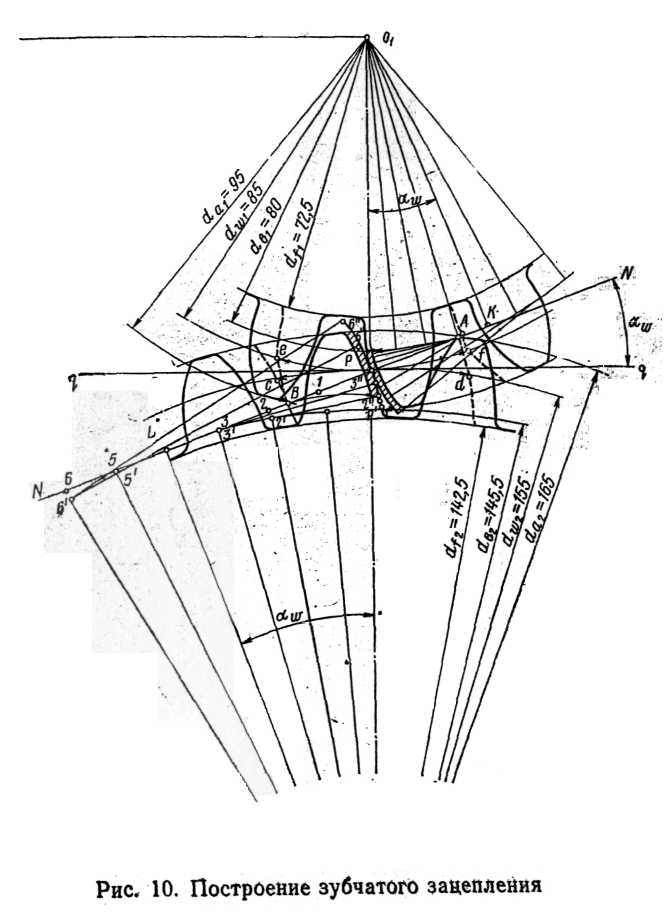
2. Проводим линию центров, отмечаем на ней центры О₁ и О₂ на расстоянии а_а =a_w/k_l=120/0,375 = 320 мм

(центры колес О₁ и О₂ могут выходить за пределы чертежа).

3. В выбранном нами масштабе вычерчиваем окружности зубчатых колес: основные, начальные, окружности высту­пов и впадин

Масштабные значение расчетных параметров

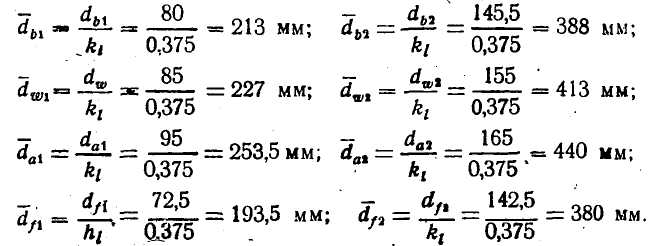
. 4. Через полюс зацепления Р проводим общую касатель­ную к начальным окружностям перпендикулярно к линии центров) и линию зацепления NN, касательную к основным окружностям, при этом угол a_w между этими касательными должен быть равен а_w =20°.

5. Проведем перпендикуляры О₁К и O₂L из центров О₁О₂ ,к линии зацепления (длины этих перпендикуляров есть ра­диусы основных окружностей).

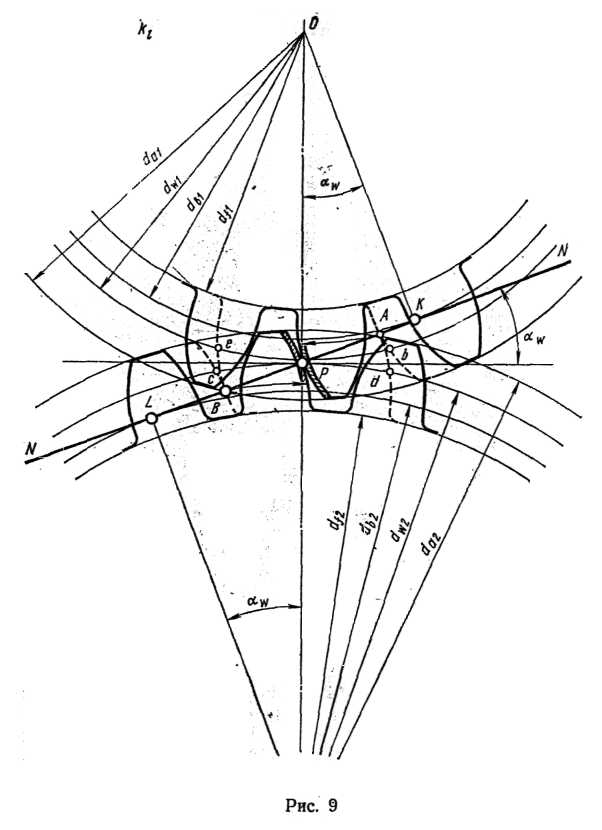
Участок KL линии зацепления называется теоретическим участком линии зацепления.

6. Каждый зуб зубчатого колеса находится в зацеплении не на всем своем пути, а только на каком-то участке, т. е. в какой-то точке он входит в зацепление, а в какой-то выходит из него. Этот участок, лежащий на линии зацепления NN и образованный пересечением этой линии с. окружностями выступов_; называется практическим или рабочим участком ли­нии зацепления. На рис. 9 практический участок линии, за­цепления обозначен точками А и В.

7. Строим эвольвентныё профили только центральной па­ры сопряженных зубьев так, чтобы они касались в полюсе за­цепления Р (рис. 8).

Эвольвентной окружности называется кривая, описывае­мая точкой прямой линии, перекатываемой по этой окружно­сти без скольжения! Окружность, по которой перекатывается прямая при образовании эвольвенту, называется основной окружностью. Следовательно, эвольвентныё участки зубьев будут находиться в пределах между основными окружностя­ми и окружностями выступов колес.

Построение эвольвенты производим общепринятым мето­дом. Для этого отрезок LP линии зацепления (второго коле­са) разбиваем на равное число частей (допустим, на четыре), обозначим точки деления 1, 2, 3, 4 и т. д., продолжив деление по другую сторону точки L.

Отрезок LP линии зацепления играет роль производящей прямой, при обкатывании которой без скольжения по основ­ной окружности точка Р опишет эвольвенту.

Полученные отрезки Р—1,1—2, 2—3 . . ., начиная от точ­ки L, отложим по хорде на основной окружности, при этом разностью между длинами дуги и хорды пренебрегаем. Полу­ченные точки обозначим 1¹, 2', 3' . . .

Соединим эти точки с центром колеса и проведем через них касательные к основной окружности, которые будут пер­пендикулярны радиусам.

Отложим на касательных отрезки, равные расстоянию до полюса Р от соответствующей точки деления, т. е. вдоль пер­вой касательной откладываем отрезок Р—1, вдоль второй касательной — отрезок Р—2 и т.д. Полученные точки обозна­чим 1", 2", 3" и. затем последовательно соединим их плавной кривой. Данная кривая и будет представлять эвольвентный участок профиля зуба. Для сопряженного колеса эвольвентный профиль зуба строится аналогично.

Неэвольвентный участок профилей зубьев, т. е. участок в пределах от основной окружности до окружности впадин, для случая d_f<^d_b очерчивается радиальными прямыми, после чего у основания зуба производят их сопряжение с окружно­стями впадин радиусом р= (0,2÷0,3)m.

Если df~>db, то сначала получают точку пересечения ок­ружности впадин в эвольевентной, а затем у основания дела­ют закругления радиусам p = (0,2÷0,3) m. .

Для построения симметричного профиля зуба отложим

k₁=(S=S/k₁=7,85/0,375=21 мм)

проведем ось симметрии и затем методом зеркальной симмет­рии и шаблонов строим профиль зуба (рис. 9),

Аналогично производится построение профилей соседних зубьев.

Обозначим рабочие участки профилей зубьев. Учитывая, что в точке А начинается зацепление, т. е. в ней контактируются крайняя точка головки зуба второго (большого) коле­са и наинизшая точка ножки зуба первого (малого) колеса, радиусом О₁А сделаем засечку на профиле зуба малого коле­са, которая определит нам положение наинизшей точки первого колеса. Делая засечку на профиле зуба второго (боль­шего) колеса радиусом! О₂В, определим наинизшую точку, участвующую в зацеплении, для этого колеса. Рабочие участ­ки профилей зубьев на чертеже отмечены утолщенной линией.

Определим длину дуги зацепления по любой из окружно­стей, в пределах которой происходит зацепление зубьев, пред­варительно проведя пунктиром через точки А и В сопряжен­ные профили в положении начала и конца зацепления. Дуги cd и ef между положениями, соответствующих профилей зубь­ев в начале и конце зацепления для каждого из колес есть пу­ти, проходимые зубьями за время зацепления одной пары зубьев, измеренные по начальной окружности. Эти дуги и на­зываются дугами зацепления.

В общем геометрическая картина нормального эвольвентного зубчатого зацепления двух колес с учетом построения эвольвентного профиля зубьев представлена на рис. 10.

При работе зубчатых колес необходимо, чтобы в любой момент времени зубья находились в зацеплении.

Для этого требуется, чтобы дуга зацепления была больше шага. В про­тивном случае первая пара зубьев выйдет из зацепления раньше, чем войдет в зацепление следующая пара зубьев.

Отношение дуги зацепления к шагу характеризуется коэф­фициентом перекрытия е.

Определим коэффициент перекрытия графическим и аналитическим методами.

На основании Данного выше определения запишем

(величина АВ находится при измерении на чертеже).

Для определения коэффициента перекрытия аналитическим методом имеем:

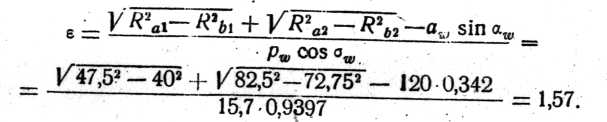
Вычислим процент расхождения

Полученный процент расхождения не превышает допуска­емой величины.

РЕКОМЕНДУЕМАЯ ЛИТЕРАТУРА

1 Артоболевский И. И; Теория механизмов и машин. М.: Нау­ка, 1975

2. Артоболевский И..И., Эдельштейн Б. В, Сборник задач по теории механизмов и машин. М.: Наука, 1972.

3. Теория механизмов и машин. Учебник для вузов Под ред. К. В. Фролова. М..: высшая школа. 1987.

4. Иосилевич Г. Б. Прикладная механика. М.: Высшая школа,1987.

Кандидаты техн. наук, доценты Ю. И. БИТЮЦКИП, Г. П. НОСКОВ, В. Г. МИЦКЕВИЧ

ПРИКЛАДНАЯ МЕХАНИКА Часть I

Теория механизмов и машин

Методические указания к выполнению контрольной работы №

Редактор К. Г. Никольская

Техн. редактор Н. Н. Соловьева

Корректор О. И. Вартанян

Сдано в набор 23.03.1988. Подписано в печать 29.И. 1088. Тираж 9000. Гарнитура литературная. Печать высокая. Формат 60X90'/i».

Печ. л. 1,5. Уч.-изд. л. 1,75. Тип, за«. 321, Изд. зак. 549.- Бесплатно.

Редакционно-издат. отдел, типография ВЗИИТа, Д25808, Москва, ГСП-47* ул. Часовая, 22/2