4. Определение угловых ускорений звеньев механизма
Угловые ускорения звеньев определяются на основе построенного плана.
Звено 1. Ведущее звено вращается равномерно с постоянной угловой скоростью. Следовательно, его угловое ускорение
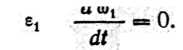
Звено 2. Абсолютная величина углового ускорения звена
2 может быть получена через тангенциальное ускорение atB/A по формуле
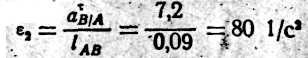
и направлено против часовой стрелки. Чтобы определить направление углового ускорения ε2, необходимо вектор относительного тангенциального ускорения atB/A с плана ускорений (на плане ему соответствует вектор n1b) перенести в точку В механизма, а точку A условно закрепить, тогда вектор atB/A будет вращать точку В звена 2 относительно точки А против часовой стрелки, а следовательно, и угловое ускорение будет направлено против часовой стрелки.
Звено 3. Угловое ускорение третьего звена определяется аналогично и будет равно
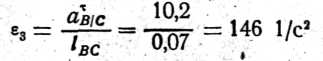
и направлено против часовой стрелки (в этом также легко
убедиться, если вектор atB/C перенести в точку В механизма).
Направление угловых ускорений для всех звеньев указано на схеме механизма (рис.1). .
Таким образом, основная задача кинематического исследования — определение скоростей и ускорений звеньев механизма — выполнена.
В некоторых механизмах (например, в механизме, представленном на схеме II, см. задание на задачу № 1 контрольной работы № 1) при движении возникает дополнительное, так называемое поворотное, или кориолисово ускорение.
Из теоретической механики известно, что кориолисово ускорение имеет место при движении тел относительно переменного поля скоростей.
Рассмотрим пример (в общем виде) построения плана ускорений для аналогичного механизма, представленного на рис. 5. План скоростей этого механизма при заданном положении изображен на рис. 6 и строится методом, описанным выше
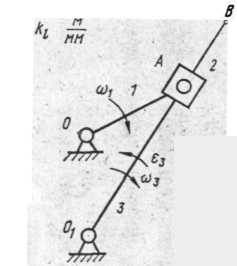
Рис.5 Схема кулисного механизма
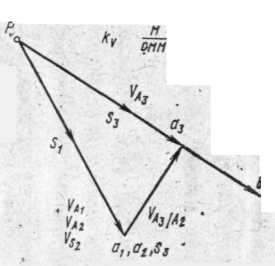
Рис.6 План скоростей кулисного механизма
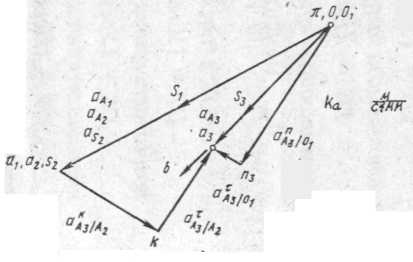
Рис.7 План ускорений кулисного механизма
Как и в предыдущем примере, первой точкой, ускорение которой надо определить, является точка А ведущего звена (т. е. точка А).
Напишем векторное уравнение
Так как звено l вращается с постоянной угловой скоростью
(ω1 = const), то
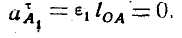
Полное ускорение аА точки А1 определяется только величиной нормального ускорения anA1 , которое равно anA1=ω12lOA и направлено параллельно звену. О А от точки А к точке О.
Следующая точка А2, т. е. точка А, принадлежащая звену 2. Точки А1 и А2 соединены жестко, поэтому их ускорения будут равны,
Точка А3 (т. е. точка А, принадлежащая звену 3) совершает сложное движение. Ее ускорение складывается из ускорений точки А2 (переносного) и ускорения точки А3 при движении звена 2 по звену 3 (относительного). С другой стороны, ускорение А3 складывается из ускорения точки О1 и относительного ускорения точки А3 при вращении звена 3 вокруг точки О1.
На основании этого, можно записать следующую, систему уравнений:
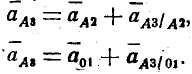
Звено 2 совершает относительное поступательное движение по звену 3, которое в свою очередь вращается вокруг точки О1
В этом случае возникает дополнительное, так называемое поворотное, или кориолисово ускорение акА3/А2 и, следовательно, полное относительное ускорение aA3/A2 следует представить в виде суммы двух составляющих:
Абсолютная величина кориолисова ускорения определяется из выражения
где Vаз/а2 - линейная скорость относительного движения тела, м/с;
ωз — угловая скорость переносного движения c-1
Для определения направления акА3/А2 следует воспользоваться правилом умножения векторов, согласно которому вектор акА3/А2 будет направлен в ту сторону, в которую окажется направленным векторVA3/A2, если его повернуть на 90° в направлении угловой скорости ωз.
Вектор касательного ускорения atA3/A2 направлен так же, как и вектор относительной скорости VA3/A2 т. е. параллельно звену 3.
Относительное ускорение аA3/О1 как и в предыдущем примере, представлено в виде суммы двух составляющих — нормальной и тангенциальной
Абсолютная величина нормального ускорения равна:
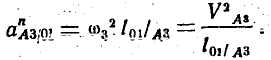
Нормальное ускорение аnA3О1 направлено вдоль звена O1A3 от точки A3 к точке О1 (центру вращения).
Тангенциальная составляющая аtA3/O1 по абсолютной величине неизвестна, но известна по направлению. Она направлена перпендикулярно нормальной составляющей.
Ускорение точки A2 — aA2—нам, известно и по величине и по направлению, а ускорение точки O1— a01 =0.
Следовательно, наша система имеет две неизвестные величины и может быть решена графическим методом, путем построения плана ускорения.
Для этого выбираем на плоскости произвольную точку π (рис. 7) полюс плана ускорений, которая является началом отсчета, и откладываем от нее отрезок πах параллельно ОА в направлении от точки А к точке О, в соответствии со схемой механизма. Длина этого отрезка изображает на плане ускорений вектор ускорения точки А1— аА2 и выбирается произвольно, исходя из удобства размещения на чертеже. Приняв длину отрезка πа1 определенной величины; мы определим масштабный коэффициент плана ускорений по формуле
В соответствии с вышеизложенным: этот же отрезок в масштабе будет изображать вектор ускорения точек А2 и S2 центра тяжести звена 2 (на плане ускорений они отмечены точками а2 и s2).
Затем через точку a1 плана ускорений проводим прямую и на ней откладываем отрезок (a1k) = (akA3/A2)/(ka) величина которого в масштабе соответствует величине вектора кориолисова ускорения akA3/A2.
Предварительно, для того чтобы определить линию действия, а затем и направление кориолисова ускорения, необходимо взять вектор относительной скорости VA3/A2 условно перенести его в точку a1 плана ускорений и повернуть на 90° в направлении угловой скорости ω3, т.е. по часовой стрелке. Положение вектора VA3/A2 будет определять направление кориолисова ускорения.
Через точку k параллельно звену 3 (или, что то же самое, перпендикулярно а1k) проводим линию действия вектора тангенциального ускорения аtA3/A2 .
Строим сумму векторов, второго уровня. Из полюса (точка О1 совпадает с полюсом) проводим прямую, параллельную звену 3 в направлении от точки Аз к точке О1, и откладываем на плане отрезок
(πn3)=(anA3/O1)/(ka)
который в масштабе равен модулю вектора нормального ускорения.
Через точку n3 перпендикулярно звену 3 проводим линию действия вектора тангенциального ускорения atA3/O1.
Пересечение на плане ускорений двух прямых, изображающих линии действия тангенциальных ускорений, дает точку а3.Соединяя точку а3 с полюсом плана ускорений π, получим отрезок (πа3) соответствующий на плане вектору ускорения точки Аз, величина которого равна:
аА3=(πа3)ка.
Из плана ускорений можно определить по абсолютной величине все неизвестные нам ускорения.
Весь дальнейший расчет выполняется аналогично тому, как это было сделано в первом примере.