Методические указания к выполнению контрольной работы № I

Контрольная работа № 1 состоит из двух задач.

Первая задача посвящена структурному и кинематическо­му исследованию механизма. Во второй задаче производится расчет и построение геометрической картины нормального эвольвентного зацепления двух зубчатых колес.

Прежде чем приступить к выполнению контрольной рабо­ты, студент должен предварительно изучить следующие ос­новные вопросы:

1. Структурный анализ механизмов.

1. Исследование и проектирование плоских рычажно-шарнирных механизмов.

2. Кинематический анализ механизмов. Задачи и методы кинематического анализа. Планы положений механизма. Оп­ределение скоростей и ускорений методом планов. Кинемати­ческие диаграммы.

4. Зубчатые передачи. Виды зубчатых механизмов. Пере­даточное отношение. Основы теории зацепления. Элементы и параметры стандартного эвольвентного зацепления.

Задача №.1 структурное и кинематическое исследование механизма

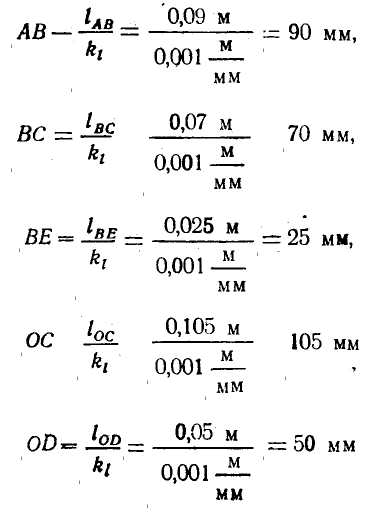
В качестве примера для решения задачи № 1 контрольной работы № 1 проведем исследование схемы механизма, пред­ставленной на рис. 1, у которого ведущее звено 1 (кривошип ОА) вращается со скоростью n₁=210 об/мин по часовой стрелке; размеры механизма: l_ОА =0,04 м; l_АВ =0,09 м; l_ВС =0,07 м; l_ВЕ =0,025 м; l_0С =0,105 м; l_OD =0,05 м; моменты инерции звеньев относительно осей проходящих через центр тяжести.

угол положения ведущего звена ф=135°.

В теории механизмов и машин действительные размеры принято выражать в метрах, а их масштабные значения — в миллиметрах.

По исходным данным вычерчиваем схему механизма в произвольно выбранном, но удобном для построения масшта­бе k_l м/мм, где k_l— масштабный коэффициент, который показывает, сколько метров действительной длины содержит­ся в одном миллиметре отрезка на чертеже.

Действительная длина ведущего звена l_0А =0,04 м. На чертеже изобразим его отрезком ОА = 40 мм. Тогда масштаб­ный коэффициент будет равен

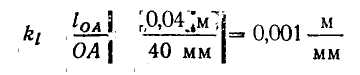
В этом масштабе вычерчиваем схему механизма.

Чертежные размеры в мм остальных звеньев в выбранном масштабе определятся соответственно:

Структурное и кинематическое исследование механизма

I. Структурное исследование механизма

Согласно принципу образования механизмов, сформули­рованному впервые русским ученым Л. В. Ассуром, любой механизм может быть составлен последовательным присое­динением к ведущему звену (ведущим звеньям) групп звень­ев с нулевой степенью подвижности.

Определим количество ведущих звеньев нашего механиз­ма. Как известно, оно определяется степенью подвижности W механизма, которая может быть вычислена по формуле академика П. Л. Чебышева

W=3n-2p₅-p₄,

где n— число подвижных звеньев; p₅ .— число низших ки­нематических пар; р₄ — число высших кинематических пар.

Исследуемый механизм имеет: число подвижных звеньев n=3 (на схеме механизма все подвижные звенья пронумеро­ваны от 1 до 3, а неподвижное звено-стойка обозначено че­рез 0); число низших кинематических пар p₅=4. Высших ки­нематических пар р₄ в данном механизме нет.

Следовательно, степень подвижности его равна:

W=3*3-2*4=1.

Это означает, что в рассматриваемом механизме доста­точно задать закон движения только одному звену (в данном случае звену l, которое является ведущим), чтобы закон дви­жения всех остальных звеньев был бы вполне определенным.

Произведем разложение механизма на группы Ассура. Правильно выполнить эту операцию очень важно, так как с этим непосредственно связано все дальнейшее исследование механизма.

Разложение механизма на группы Ассура обычно осуще­ствляется методом попыток и его следует начинать с послед­ней, наиболее отдаленной от ведущего звена и наиболее про­стой группы. Простейшая группа Ассура представляет собой сочетание двух звеньев и трех кинематических пар.

Для нашего механизма такой группой является комбина­ция звеньев 2 и 3 и трех вращательных кинематических пар: в точках А, В к С.

Действительно, оставшаяся часть механизма — ведущее звено ОА — имеет степень подвижности W=1. Группа 2—3 является труппой Ассура первого вида, так как все три ки­нематические пары являются вращательными.

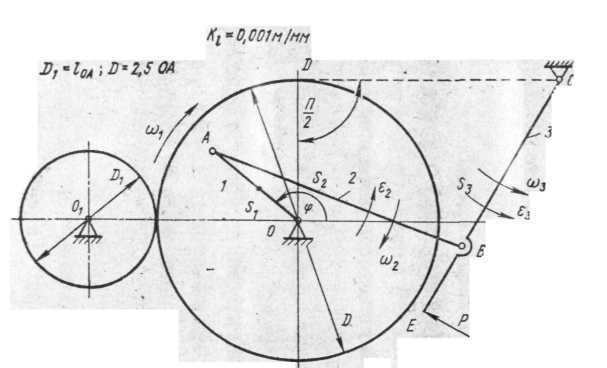
Рис.1 Схема механизма

Рис.2 Разложение механизма на группы Ассура