Экономико-математические модели и методы управления проектами

Курсовая работа Построение производственной функции и оценка ее адекватности

МІНІСТЕРСТВО ОСВІТИ І НАУКИ МОЛОДІ ТА СПОРТУ УКРАЇНИ

НАЦІОНАЛЬНИЙ УНІВЕРСИТЕТ КОРАБЛЕБУДУВАННЯ

імені адмірала Макарова

Кафедра Управління проектами

Методичні вказівки до виконання курсової роботи з дисципліни “Економіко-математичні моделі та методи управління проектами ”

для студентів спеціальності «Управління проектами»

Миколaїв-2012

ЗМІСТ

ВСТУП 3

1 Мета та завдання курсової роботи 4

2 Структура звіту з курсової роботи 5

3 Календарний план виконання роботи та принципи оцінювання 6

4 Короткі теоретичні відомості 7

5 Варіанти завдання 19

6 Литература 22

ВСТУП

В процесі виконання курсових робіт у студентів виникають такі типові питання:

• вибір теми і підготовка завдання на курсову роботу;

• організація роботи, основні вимоги до курсової роботи, форма представлення результатів;

• вимоги до змісту і оформлення пояснювальної записки;

• порядок захисту курсової роботи.

У даних вказівках стисло розглянуті відповіді на означені питання до виконання курсової роботи з дисципліни “Економіко-математичні моделі та методи управління проектами ” для студентів, що навчаються за спеціальністю “Управління проектами ”.

1Мета та завдання курсової роботи

Мета курсової роботи : Здобуття студентами навичок побудови виробничої функції (ВФ) за експериментальними даними про витрати-випуски.

В процесі виконання роботи, студент повинен виконати наступні завдання:

1. Привести виробничу функцію (ВФ) Кобба-Дугласа до лінійного виду.

2. Скористатися таблицею згідно з отриманим варіантом, в якій приведені динамічні ряди по випуску продукції і витрат ресурсів

3. Визначити коефіцієнти множинної регресії по методу МНК

4. Визначити коефіцієнти множинної регресії за допомогою табличного процесора

   1. Створити лист з ім'ям "Регресійний аналіз";

   2. Провести математичне формулювання завдання у вигляді таблиці початкових даних.

   3. Запустити пакет регресійного аналізу через меню "Сервіс - Пакет аналізу - Регресія".

   4. У вікні "Регресія" задати інтервали, що містять, Y і X. Результати обробки розташувати на листі "Регресійний аналіз".

5. Здійснити зворотне перетворення

6. Визначити коефіцієнт множинної детерміації.

7. Побудувати графік виробничої функції.

8. Зробити висновок.

2Структура звіту з курсової роботи

Звіт з курсової роботи містить::

• електронний файл з розрахунками у форматі будь-якого математичного пакету

• розрахунково-пояснювальну записку.

Структура розрахунково-пояснювальної записки містить наступні пункти:

1. Титульний аркуш;

2. Завдання на курсову роботу;

3. Анотація (українською, російською);

4. Зміст;

5. Перелік умовних означень (у разі потреби);

6. Вступ (актуальність теми, мета та завдання роботи, структура роботи);

7. Теоретична частина (Розділ 1)( теоретичні відомості по роботі);

8. Розрахункова та графічна частина(Розділ 2);

9. Висновки;

10. Список використаної літератури;

11. Додатки (у разі потреби).

3Календарний план виконання роботи та принципи оцінювання

№	Назва етапу курсової роботи	Термін виконання, тиждень	Кількість балів
1	Визначення актуальності теми, цілей роботи	9	5-10
2	Вивчення теоретичного матеріалу	10	5-10
3	Логарифмування ВФ, приведення до лінійного виду	11	10-13
4	Визначити коефіцієнти множинної регресії по методу МНК	12	10-15
	Визначити коефіцієнти множинної регресі за допомогою Excel	13	5-10
5	Зворотне перетворення та оцінювання коефіцієнту множинної детерміації	14	5-10
	Побудова графіків	15	5-10
6	Висновки по роботі	17	10-12
7	Оформлення результатів	18	5-10
Всього			60-100

4Короткі теоретичні відомості

У сучасному суспільстві виробництво — важлива сфера бізнесової діяльності, основні джерело отримання благ, які необхідні для життя людини забезпечення її зростаючих потреб. Там, де люди створюють якийсь продукт, існує виробництво. Всі фірми прагнуть отримувати максимальний прибуток, для чого змушені ефективної вести виробництво, тобто використовувати такі методи, які були б вигідними які технологічно, так і економічно.

Для здійснення виробничої діяльності фірмі необхідні фактори виробництва, які протягом виробничого циклу трансформуються у вихідну або готову продукцію.

Виробнича функція виражає функціональну залежність між вхідними ресурсами і випуском готової продукції (обсягом виробництва); вона підкреслює, що вихід продукції є лише функцією кількості вхідних факторів, які використовуються у виробничому процесі.

Виникнення теорії виробничих функцій прийнято відносити до 1928г., коли з'явилася стаття американських учених економіста П. Дугласа і математика Д. Кобба "Теорія виробництва". У цій статті, була зроблена спроба, емпіричним шляхом визначити вплив капіталу, що витрачається, і праці на об'єм продукції, що випускається, в оброблювальній промисловості США.

Теорія виробництва базується на використанні факторних моделей, що пов'язують величину результату виробництва з обсягами виробничих факторів, які обумовили цей результат.

Найпоширенішим видом таких факторних моделей є виробничі функції. В загальному вигляді виробнича функція може бути предста­влена формулою:

Q= f (L,K,M,…),

де L, К, М — вхідні фактори виробництва: праця, капітал, матеріали та ін.

Виробнича функція, як і будь-яка економічна модель, є певним спрощенням дійсності. Наприклад, праця може описуватися не одним числом, а сукупністю чисел, оскільки у процесі виробництва використовуються працівники різних про­фесій, кваліфікації, різного вікового складу тощо.

Виробнича функція показує максимально можливий випуск продукції, який може виробити фірма при кожному конкретному поєднанні мінімально не­обхідної кількості факторів виробництва.

Д. Коббом була запропонована виробнича функція виду

F = dK^L^ (1)

де F - об'єм випущеної продукції;

K - об'єм основного капіталу (основні фонди);

L - витрати праці (чисельність зайнятих);

d, , - числові параметри; d>0, , 0.

При побудові виробничої функції Кобба-Дугласа параметри C, ,  можна оцінити за допомогою лінійного регресійного аналізу по методу найменших квадратів (МНК) :

Виробничу функцію Кобба-Дугласа (1) приводять до лінійного виду шляхом логарифмування

(2)

При застосуванні МНК мета полягає в мінімізації суми квадратичних відхилень (SSD) між спостережуваними величинами ln(F) і відповідними оцінками ln( ), де - теоретичне значення випуску, отримане по формулі (1)

(3)

Введемо підстановки:

ln(F)=y

ln(K)=x1

ln(L)=x2 (4)

ln(d)=a

=b, =c

C обліком підстановок рівняння (2) набере вигляду

y=a+bx₁+cx₂ (5)

що відповідає лінійній функції двох змінних.

Суммa квадратичних відхилень (SSD) в цьому випадку запишеться як

Для того, щоб мінімізувати SSD знаходимо її приватні похідні по змінних а, в, с і потім прирівнюємо їх нулю.

Розкриваючи дужки і прирівнюючи кожну похідну до нуля. Отримуємо стсему рівнянь 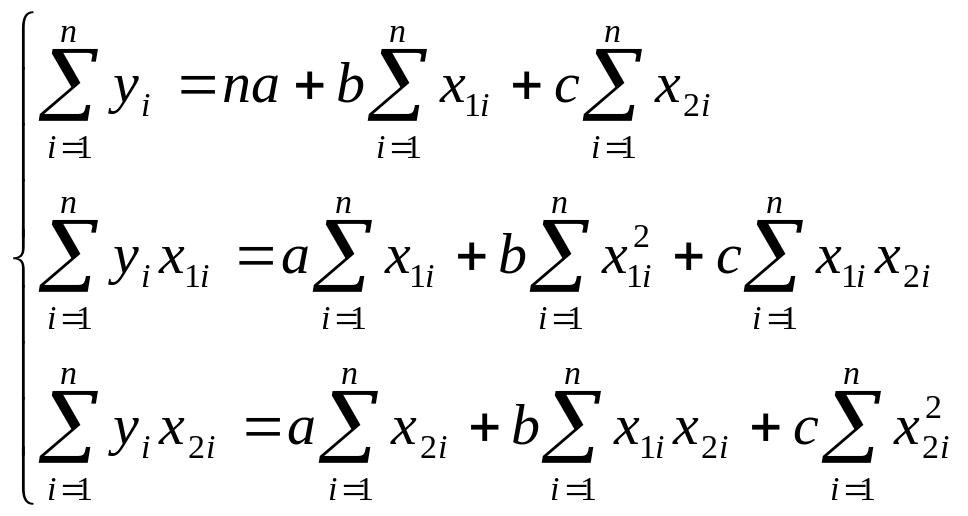(6)

(6)

Вирішуємо систему (6) відносно а, в, с.

Використовуючи зворотні підстановки (4), записуємо (1) в числовому вираженні

Для оцінки адекватності регресивної моделі спостережуваним величинам обсягу випуску F розраховується коефіцієнт множинної детермінації :

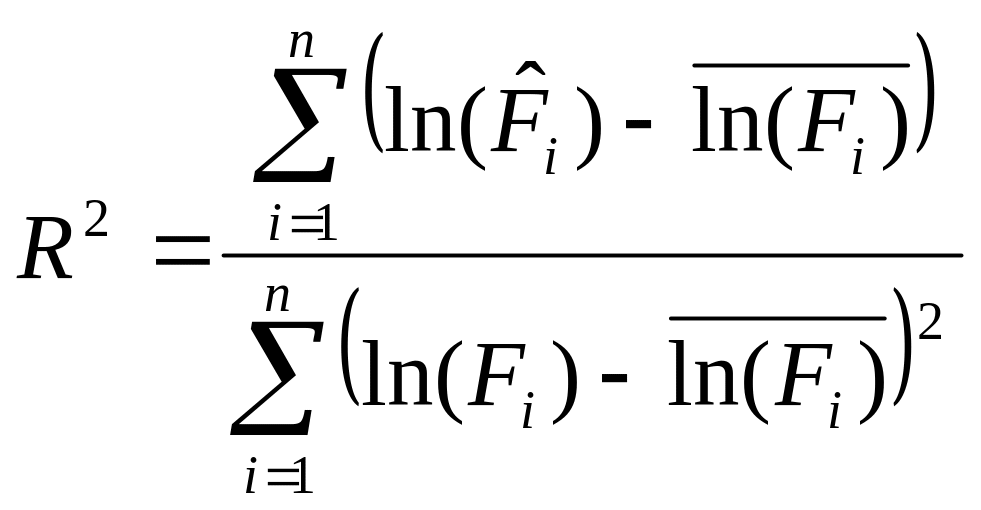
де .

Чим менше відрізняється R² від одиниці, тим більше обґрунтовано рішення про те, що вибіркові коефіцієнти регресії можуть бути корисні для вивчення виробничого процесу.

Використання Microsoft Office Excel для аналізу даних

Електронний процесор Excel дозволяє будувати математичні моделі за наявними табличними даними. Математична модель дає можливість прогнозувати стан модельованого об'єкту і вибирати на цій основі оптимальне управління об'єктом. Для цих цілей Excel містить пакет аналізу даних, в який входять, : регресійний аналіз, кореляція, дисперсійний аналіз і інші засоби.

Регресійний аналіз

Регресійний аналіз дозволяє отримати функціональну залежність між деякою випадковою величиною Y і деякою впливаючою на Y величинами X. Така залежність дістала назву рівняння регресії. Розрізняють просту (парну) і множинну регресію лінійного і нелінійного типу.

Приклад простої лінійної регресії :

y=m1x+b.

Приклад множинної лінійної регресії :

y=m1x1+m2x2+.. + mkxk+b. 1)

Для оцінки міри зв'язку між величинами використовується коефіцієнт множинної кореляції R Пірсону (кореляційне відношення), який може набувати значень від 0 до 1. R=0 якщо між величинами немає ніякого зв'язку і R=1, якщо між величинами є функціональний (детермінована) зв'язок. В більшості випадків R набуває проміжних значень від 0 до 1. Величина R2 називається коефіцієнтом детерміації.

Завданням побудови регресійної залежності є знаходження вектора коефіцієнтів M моделі (1) при якому коефіцієнт R набуває максимального значення.

Для оцінки значущості R застосовується F -критерий Фишера, обчислюваний за формулою:

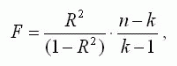
де n - розмір вибірки (кількість експериментів); k - число коефіцієнтів моделі. Якщо F перевищує деяке критичне значення для даних n і k і прийнятій довірчій вірогідності, то величина R вважається істотною. Таблиці критичних значень F приводяться в довідниках за математичною статистикою.

Таким чином, значущість R визначається не лише його величиною, але і співвідношенням між кількістю експериментів і кількістю коефіцієнтів (параметрів) моделі. Дійсно, кореляційне відношення для n=2 для простої лінійної моделі дорівнює 1 (через 2 точки на площині можна завжди провести єдину пряму). Проте, якщо експериментальні дані є випадковими величинами, довіряти такому значенню R слідує з великою обережністю. Зазвичай для отримання значущого R і достовірній регресії прагнуть до того, щоб кількість експериментів істотно перевищувала кількість коефіцієнтів моделі (n>>k).

Для побудови лінійної регресійної моделі необхідно:

1) підготувати список з n рядків і m стовпців, що містить експериментальні дані (стовпець, що містить вихідну величину y має бути або першим, або останнім в списку);

2) звернутися до меню Сервіс/Аналіз даних/Регресія

Якщо пункт "Аналіз даних" в меню "Сервіс" відсутній, то слід звернутися до пункту "Надбудови" того ж меню і встановити прапорець "Пакет аналізу".

3) в діалоговому вікні "Регресія" задати:

• вхідний інтервал Y;

• вхідний інтервал X;

• вихідний інтервал - верхній лівий осередок інтервалу, в який поміщатимуться результати обчислень (рекомендується розмістити на новому робочому листі);

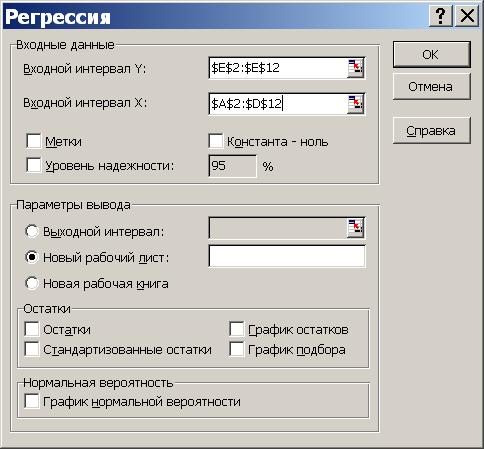
4) натиснути "Ok" і проаналізувати результати.

Приклад використання множинної лінійної регресії

Припустимо, що забудовник оцінює вартість групи невеликих офісних будівель в традиційному діловому районі.

Забудовник може використовувати множинний регресійний аналіз для оцінки ціни офісної будівлі в заданому районі на основі наступних змінних.

y - оцінна ціна будівлі під офіс;

x1 - загальна площа в квадратних метрах;

x2 - кількість офісів;

x3 - кількість входів (0,5 входу означає вхід тільки для доставки кореспонденції);

x4 - час експлуатації будівлі в літах.

В даному прикладі передбачається, що існує лінійна залежність між кожною незалежною змінною (x1, x2, x3 і x4) і залежною змінною (y), тобто ціною будівлі під офіс в цьому районі. Початкові дані показані на малюнку.

Налаштування для вирішення поставленого завдання показані на малюнку вікна "Регресія". Результати розрахунків розміщені на окремому листі в трьох таблицях

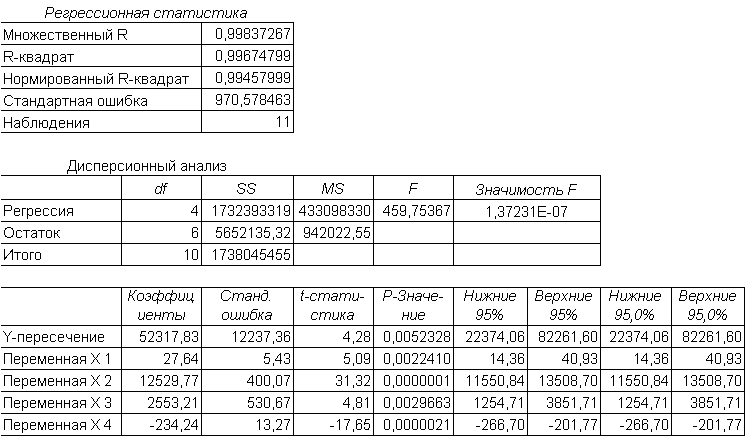
У результаті ми отримали наступну математичну модель:

y = 52318 + 27,64*x1 + 12530*x2 + 2553*x3 - 234,24*x4.

Тепер забудовник може визначити оцінну вартість будівлі під офіс в тому ж районі. Якщо ця будівля має площу 2500 квадратних метрів, три офіси, два входи і час експлуатації - 25 років, можна оцінити його вартість, використовуючи наступну формулу:

y = 27,64*2500 + 12530*3 + 2553*2 - 234,24*25 + 52318 = 158 261 у.о.

У регресійному аналізі найбільш важливими результатами являються:

• коефіцієнти при змінних і Y -пересечение, моделі, що є шуканими параметрами;

• множинний R, що характеризує точність моделі для наявних початкових даних;

• F -критерий Фишера (у розглянутому прикладі він значно перевершує критичне значення, рівне 4,06);

• t -статистика - величини, що характеризують міру значущості окремих коефіцієнтів моделі.

На t -статистике слід зупинитися особливо. Дуже часто при побудові регресійної моделі невідомо, впливає той або інший чинник x на y. Включення в модель чинників, які не впливають на вихідну величину, погіршує якість моделі. Обчислення t -статистики допомагає виявити такі чинники. Наближену оцінку можна зробити так: якщо при n>>k величина t -статистики по абсолютному значенню істотно більше трьох, відповідний коефіцієнт слід вважати значущим, а чинник включити в модель, інакше виключити з моделі. Таким чином, можна запропонувати технологію побудови регресійної моделі, що складається з двох етапів, :

1) обробити пакетом "Регресія" все наявні дані, проаналізувати значення t -статистики;

2) видалити з таблиці початкових даних стовпці з тими чинниками, для яких коефіцієнти незначущі і обробити пакетом "Регресія" нову таблицю.

Для прикладу розглянемо змінну x4. У довіднику за математичною статистикою t -критическое з (n - k - 1)=6 ступенями свободи і довірчою вірогідністю 0,95 рівне 1,94. Оскільки абсолютна величина t, рівна 17,7 більше, ніж 1,94, термін експлуатації - це важлива змінна для оцінки вартості будівлі під офіс. Аналогічним чином можна протестувати усі інші змінні на статистичну значущість. Нижче наводяться спостережувані t -значения для кожної з незалежних змінних :

Загальна площа	5,1
Кількість офісів	31,3
Кількість входів	4,8
Термін експлуатації	17,7

Усі ці значення мають абсолютну величину більшу, ніж 1,94; отже, усі змінні, використані в рівнянні регресії, корисні для пророцтва оцінної вартості будівлі під офіс в цьому районі.

Табулювання функції двох змінних. Побудувати графіки.

Протабулюємо функцію z = , якщо x  [-5;5] , y  [-5;5] з кроком 0.5.

Ввести в А4 значення для а: 5. Ввести в В4 значення для в:5.

Ввести в В5 початкове значення для змінної X: -5 і перейти в комірку С5.

В меню Edit вибрати Fill (заповнити), вибрати Series (прогресія). У вікні , що з’явиться (Series), вибрати режим Rows ( по рядках), тип прогресії linear (арифметична). У віконце Step Value (крок) ввести 0,5; у віконце Stop Value (кінцеве значення) ввести 5. Клацнути по кнопці <OK>.

П’ятий рядок заповниться рядом значень від -5 до 5 з кроком 0,5.

Ввести в А6 початкове значення для змінної Y: -5.

В меню Edit вибрати Fill (заповнити), вибрати Series (прогресія). У вікні , що з’явиться (Series), вибрати режим Columns ( по стовпцях), тип прогресії linear (арифметична). У віконце Step Value (крок) ввести 0,5; у віконце Stop Value (кінцеве значення) ввести 5. Клацнути по кнопці <OK>.

Перший стовпчик заповниться рядом значень від -5 до 5 з кроком 0,5.

Ввести в В6 формулу: =(B$5/$A$4)^2+($A6/$B$4)^2.

Виділити комірку В6 і скопіювати формулу на шостий рядок. Не відміняючи виділення, встановити вказівник миші в правий нижній кут останньої комірки в рядку 6, і скопіювати формули на всі рядки по рядок 26 включно.

Побудуємо діаграму типу Поверхня по області В6:V26. (Рис 1)

Для цього викликати Майстра діаграм, вказати місце, де беде розташована діаграма, вказати область, по якій будується діаграма, вказати тип діаграми (Поверхня), клацнути по кнопці <Finish>.

Відредагувати діаграму: зняти легенду, надписи по осях, заливку з основи і стінок. Щоб зняти надписи по осях, потрібно: Перейти в режим редагування діаграми - двічі клацнути по ній лівою кнопкою миші. Клацнути лівою кнопкою миші на осі. З’являться чорні квадратики на кінцях осі, тобто ми перейшли в режим редагування осі.

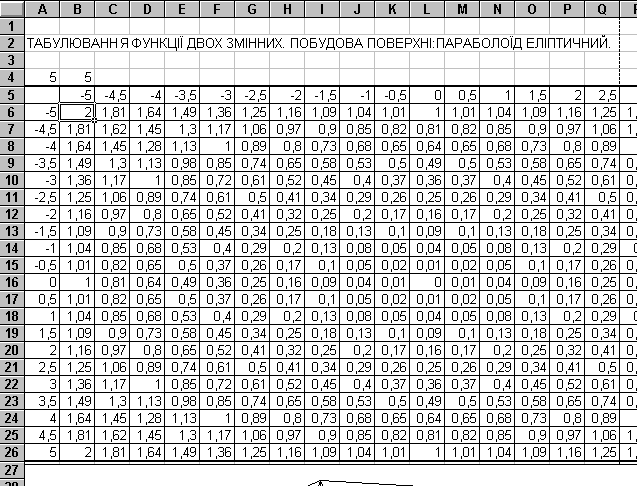
Рисунок 1. Вихідні данні для побудови діаграми.

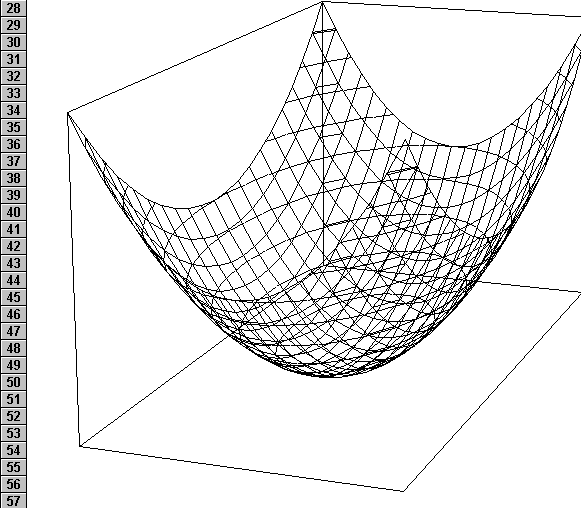
Протабулювати функцію Z= в тій самій області з кроком 0,5.

Скопіюємо таблицю на інший лист. В комірці, де введено формулу, замінити знак «+» на знак «-« . Побудувати діаграму типу Поверхня, відредагувати її як в попередньому прикладі.