
- •Математика
- •Рецензент: д-р. Физ.-мат. Наук, доцент н. П. Степанов.
- •Оглавление
- •Основные вопросы программы Тема 1. Аналитическая геометрия на плоскости
- •Тема 2. Предел функции
- •Тема 3. Дифференциальное исчисление и его приложения
- •Тема 4. Интегральное исчисление и его приложения
- •Тема 5. Дифференциальные уравнения
- •Тема 6. Функции нескольких переменных
- •Тема 7. Числовые и степенные ряды
- •Правила выполнения и оформления контрольных работ
- •Правила выбора варианта
- •Контрольной работы 1
- •Контрольной работы 2
- •Задания контрольной работы 1
- •Задания контрольной работы 2
- •Библиографический список Основная литература
- •Дополнительная литература
- •Учебно–методическое издание
- •Математика
- •В авторской редакции
- •672086, Г. Чита, ул. Ленинградская, 16.
Задания контрольной работы 1
Задачи 1 – 10
Даны вершины треугольника А, В, С треугольника. Найти:
а) скалярное
произведение
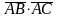 ;
;
б) внутренний угол
 ;
;
в) уравнение высоты,
проведенной через вершину
 ;
;
г) уравнение медианы, проведенной через вершину ;
д) точку пересечения высот;
е) длину высоты, проведенной из вершины .
Сделать чертеж.
1.
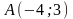 ,
,
 ,
,
 ;
;
2.
 ,
,
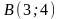 ,
,
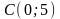 ;
;
3.
 ,
,
 ,
,
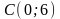 ;
;
4.
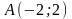 ,
,
 ,
,
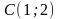 ;
;
5.
 ,
,
 ,
,
 ;
;
6.
 ,
,
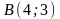 ,
,
 ;
;
7.
 ,
,
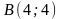 ,
,
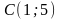 ;
;
8.
 ,
,
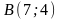 ,
,
 ;
;
9.
 ,
,
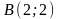 ,
,
 ;
;
10.
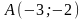 ,
,
 ,
,
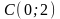 .
.
Задачи 11 – 20
Составить
уравнение линии, для каждой точки которой
отношение расстояний до точки
 и до прямой
и до прямой
 равно
равно
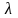 ,
если:
,
если:
11.
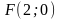 ,
,

 ,
,
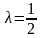 .
.
12.
 ,
,
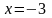 ,
,
 .
.
13.
 ,
,
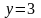 ,
.
,
.
14.
 ,
,
 ,
,
 .
.
15.
 ,
,
 ,
.
,
.
16.
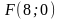 ,
,
.
,
,
.
17.
 ,
,
 ,
,
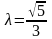 .
.
18.
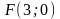 ,
,
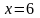 ,
,
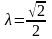 .
.
19.
 ,
,
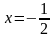 ,
.
,
.
20.
 ,
,
 ,
.
,
.
Задачи 21 – 30
Найти пределы функций:
21. 1)
 при а)
при а)
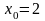 ;
б)
;
б)
 ;
в)
;
в)
 ;
;
2)
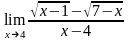 ;
;
3)
 ;
;
4)
 .
.
22. 1)
 при а)
при а)
 ;
б)
;
в)
;
;
б)
;
в)
;
2)
 ;
;
3)
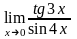 ;
;
4)
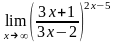 .
.
23. 1)
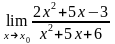 при а)
;
б)
при а)
;
б)
 ;
в)
;
;
в)
;
2)
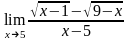 ;
;
3)
 ;
;
4)
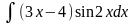 .
.
24. 1)
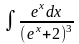 при а)
при а)
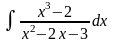 ;
б)
;
б)
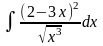 ;
в)
;
в)
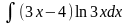 ;
;
2)
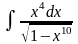 ;
;
3)
 ;
;
4)
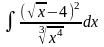 .
.
25. 1)
 при а)
при а)
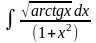 ;
б)
;
б)
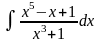 ;
в)
;
в)
 ;
;
2)
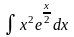 ;
;
3)
 ;
;
4)
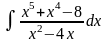 .
.
26. 1)
 при а)
при а)
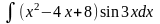 ;
б)
;
б)
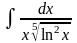 ;
в)
;
в)
 ;
;
2)
 ;
;
3)
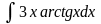 ;
;
4)
 .
.
27. 1)
 при а)
при а)
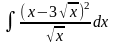 ;
б)
;
б)
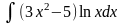 ;
в)
;
в)
 ;
;
2)
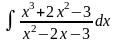 ;
;
3)
 ;
;
4)
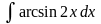 .
.
28. 1)
 при а)
при а)
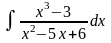 ;
б)
;
б)
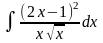 ;
в)
;
в)
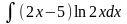 ;
;
2)
 ;
;
3)
 ;
;
4)
 .
.
29. 1)
 при а)
при а)
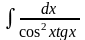 ;
б)
;
б)
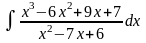 ;
в)
;
в)
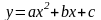 ;
;
2)
 ;
;
3)
 ;
;
4)
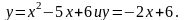 .
.
30. 1)
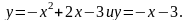 при а)
при а)
 ;
б)
;
б)
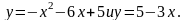 ;
в)
;
в)
 ;
;
2)
 ;
;
3)
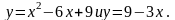 ;
;
4)
 .
.
Задачи 31 – 40
Найти производные функций:
31.
а)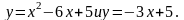 ; в)
; в)
 ;
;
б)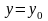 ; г)
; г)
 .
.
32.
а)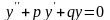 ; в)
; в)
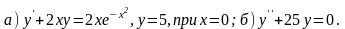 ;
;
б)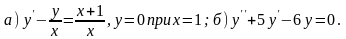 ; г)
; г)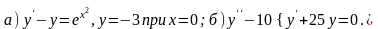 .
.
33.
а)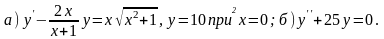 ; в)
; в)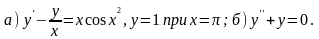 ;
;
б) ; г)
; г) .
.
34.
а)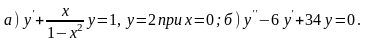 ; в)
; в) ;
;
б)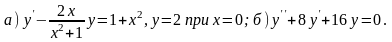 ; г)
; г)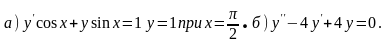 .
.
35.
а)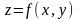 ; в)
; в) ;
;
б) ; г) .
36.
а)
; в)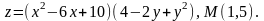 ;
;
б) ; г)
; г)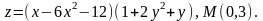 .
.
37.
а) ; в)
; в) ;
;
б) ; г)
; г) .
.
38.
а)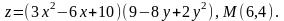 ; в)
; в)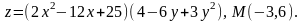 ;
;
б) ; г)
; г) .
.
39.
а) ; в)
; в) ;
;
б)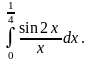 ; г)
; г)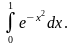 .
.
40.
а)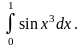 ; в)
; в)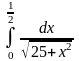 ;
;
б) ; г)
; г)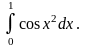 .
.
Задачи 41 – 50
Исследовать
средствами дифференциального исчисления
функцию
 и построить ее график:
и построить ее график:
41.
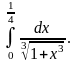 ;
;
42.
 ;
;
43.
 ;
;
44.
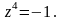 ;
;
45.
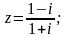 ;
;
46.
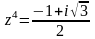 ;
;
47.
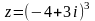 ;
;
48.
 ;
;
49.
 ;
;
50.
 .
.
Задачи 51 – 60
Вычислить
приближенное значение
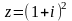 ,
заменяя приращение функции
,
заменяя приращение функции
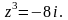 дифференциалом:
дифференциалом:
51.
 ,
,
 ;
;
52.
 ,
,
 ;
;
53.
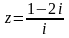 ,
,
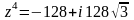 ;
;
54.
 ,
,
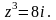 ;
;
55.
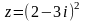 ,
,
 ;
;
56.
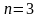 ,
,
 ;
;
57.
 ,
,
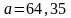 ;
;
58.
 ,
,
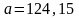 ;
;
59.
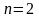 ,
,
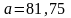 ;
;
60.
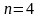 ,
,
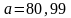 .
.
Задания контрольной работы 2
Задачи 1 – 10
Найти неопределенные интегралы. Результаты проверить дифференцированием.
1. 1) ; 3) ;
2) ; 4) .
2. 1) ; 3) ;
2) ; 4) .
3. 1) ; 3) ;
2) ; 4) .
4. 1) ; 3) ;
2) ; 4) .
5. 1) ; 3) ;
2) ; 4) .
6. 1) ; 3) ;
2) ; 4) .
7. 1) ; 3) ;
2) ; 4) .
8. 1) ; 3) ;
2) ; 4) .
9. 1) ; 3) ;
2) ; 4) .
10. 1) ; 3) ;
2) ; 4) .
Задачи 11 – 20
Вычислить площадь фигуры, ограниченной параболой и прямой . Сделать чертеж.
11.
12. .
13. .
14. .
15. .
16. .
17. .
18. .
19. .
20. .
Задачи 21 – 30
a)Найти общее решение дифференциального уравнения и частное решение, удовлетворяющее начальному условию при .
б) Найти общее решение дифференциального уравнения второго порядка .
21.
22.
23.
24.
25.
26.
27.
28.
29.
30.
Задачи 31 – 40
Даны функция и точка .
а) Найти градиент функции в точке ;
б) Исследовать функцию на экстремум.
31.
32.
33.
34.
35.
36.
37.
38.
39.
40.
Задачи 41 – 50
Вычислить приближенное значение величины , ограничиваясь тремя первыми членами ряда. Оценить погрешность.
41. 46.
42. 47.
43. 48.
44. 49.
45. 50.
Задачи 51 – 60
a) Найти модуль и аргумент комплексного числа z.
б) Найти все решения уравнения . Отметить решения на комплексной плоскости.
51. а) б)
52. а) б)
53. а) б)
54. а) б)
55. а) б)
56. а) б)
57. а) б)
58. а) б)
59. а) б)
60. а) б)
