Закон Архимеда. Плавание тел в жидкости. Свойства плавающего тела.

Закон Архимеда формулируется следующим образом[1]: на тело, погружённое в жидкость (или газ), действует выталкивающая сила, равная весу вытесненной этим телом жидкости (или газа). Сила называется силой Архимеда: Fa=pgV где p — плотность жидкости (газа), g — ускорение свободного падения, аV — объём погружённого тела (или часть объёма тела, находящаяся ниже поверхности) Pпод= γt*Vt=Gж γt – тела Vt- объем тела G –вес жидкостей вытесненной данным телом. Существует 3 свойства плавающих тел. 1 Полупогруженное состояние- подъемная сила больше массы телаРпод>Gt. 2 Погруженная состояние Рпод=Gt 3 Тело тонет Рпод<Gt Плавучесть это способность тела находиться в полупогруженном сост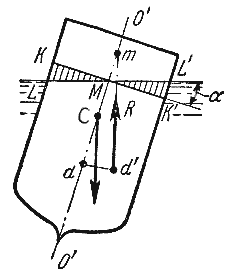оянии (второй рисунок корабл стоит ровно) тело остойчиво М – центр тяжести С – центр водоизмещения м- метоцентр. hм(от м до с на ровном корабле) > 0 тело остойчиво hм<0 тело не остойчиво hм=0 в безразличном состоянии.

Силы гидростатического давления на поверхности. Центр давления. Эпюры давления.

1.4. Сила давления жидкости на плоские поверхности Сила давления жидкости на горизонтальную поверхность равна гидростатическому давлению, умноженному на площадь ω: Pполн = (р0 + γh)ω, где Pполн – сила давления с учетом внешнего давления, измеряется в ньютонах (Н); h – глубина погружения данной горизонтальной поверхности, м. Сила манометрического давления, при условии, что внешнее давление в формуле (1.4) равно атмосферному p0 = pат, определяется по следующей формуле: P = γhω. Сила давления жидкости и центр давления на плоские стенки могут быть вычислены аналитическим и графо-аналитическим способами с помощью эпюры гидростатического давления. Аналитический способ Полная сила давления на плоскую поверхность АВСD, произвольно ориентированную (рис. 1.12), вычисляется по формуле: Pполн = p0ω + γhц.тω,. 1.6 где ω – смоченная площадь плоской поверхности АВСD, м2; γ – удельный вес жидкости, н/м3; hц.т – глубина погружения центра тяжести смоченной площади, м. Сила манометрического давления при p0 = pат находится по уравнению: Pполн = γhц.тω , 1.7 Рис. 1.12 Точка приложения равнодействующей сил манометрического давления (центр давления) для плоской поверхности АВСD, симметричной относительно оси АС (рис. 1.12), определяется по формулам (1.8) или (1.9): l∂ = J/ωlц.т, 1.8 l∂ = lц.т + J0/ωlц.т, 1.9 где l∂ – расстояние от свободной поверхности до центра давления (считая по наклону стенки), м; lц.т – расстояние от свободной поверхности (считая по наклону стенки) до центра тяжести смоченной площади, м; J – момент инерции смоченной площади относительно линии уреза жидкости; J0 – момент инерции смоченной площади относительно оси, проходящий через центр тяжести О (рис. 1.12) параллельно линии уреза воды. Центр давления (рис. 1.12) расположен на оси симметрии АС. Из формулы (1.9) видно, что центр давления расположен всегда ниже центра тяжести на величину J0/ωlц.т. 1.4.2. Графо-аналитический способ Для определения силы давления на плоскую стенку P нужно построить эпюру гидростатического давления. Тогда сила давления будет равна площади F, умноженной на ширину стенки b: P = Fb. 1.10 Формула справедлива в том случае, если ширина стенки или затвора не меняется (b = const) с изменением глубины h. Если в формулу (1.10) подставить вместо F площадь эпюры манометрического давления, то получим силу манометрического давления P, а если площадь эпюры полного гидростатического давления, то получим силу Pполн. Для нахождения центра давления нужно определить центр тяжести эпюры, из полученного центра провести линию, перпендикулярную к рассматриваемой поверхности до пересечения с ней, и измерить расстояние от этой точки до свободной поверхности. Это расстояние и даст расстояние до центра давления.