МГТУ им. Баумана

Богданов А. В.

Методические указания

к выполнению домашнего задания

по курсу “Теоретические основы лазерной обработки”

Домашнее задание №1

Под редакцией а. Г. Григорьянца

Москва 2010

Требования к выполнению домашних заданий.

Выполнение домашних заданий должно проходить в следующем порядке:

1. Знакомство с методическим указанием.

2. Изучение теоретической части методического указания.

3. Выбор исходных данных в соответствии с приведенной в конце указаний таблицы 1 и номером варианта.

4. Выбор теплофизических свойств из таблицы 2.

5. Выбор и обоснование расчетной схемы.

6. Расчет.

7. Составление отчета.

8. Защита работы.

При выполнении домашнего задания студент обязан:

1. Сформулировать основные положения выбранного метода расчета, выявить источники погрешностей и оценить точность метода.

2. Привести основные формулы и зависимости.

3. Представить результаты расчета в виде таблиц и графиков.

Отчет.

Отчет по домашнему заданию составляется индивидуально каждым студентом и должен содержать:

1. Название работы.

2. Краткое изложение теоретических основ выбранного метода расчета.

3. Расчетную схему, с обязательным показом хода лучей, направления осей координат и скорости перемещения образца. Схема должна иметь правдоподобные соотношения размеров.

4. Результаты расчетов:

   • исходные данные,

   • распечатка программы и промежуточных результатов расчетов,

   • результаты расчетов, занесенные в таблицу и построенные графики.

5. Выводы.

Для защиты работы студент должен представить правильно оформленный отчет и ответить письменно или устно на все контрольные вопросы.

Краткие сведения из теории расчета тепловых полей. Тепловые процессы при лазерной поверхностной обработке.

Решения дифференциальных уравнений теплопроводности в линейной постановке приводят к аналитическим зависимостям, простым и удобным для инженерных расчетов. При этом принимается, что теплофизические свойства материала, такие как коэффициенты теплопроводности λ_t и объемной теплоемкости c_γ, а также коэффициент теплоотдачи с поверхностей α_t не зависят от температуры. Ряд решений в теории тепловых процессов при сварке, разработанной Н.Н.Рыкалиным, можно непосредственно использовать для анализа тепловых процессов при лазерной поверхностной обработке.

При расчете температур по зависимостям, представленным ниже, следует использовать средние значения коэффициентов теплопроводности λ_t, теплоемкости c_γ и температуропроводности a (см. табл.1) обеспечивающие достаточную точность для технических целей. Указанные в таблице значения коэффициентов установлены на основании сопоставления опытных и расчетных значений температур.

Таблица 1.

Материал	Средняя температура Тср 0С	Коэффициент теплопровод ности λt, Дж/см.с.град.	Объемная теплоемкость сγ Дж/см3.град	Коэффициент температуропро водности а, см2/с
Малоуглеро дистые и низколегирован ные стали	500-600	0,38-0,42	4,9-5,2	0,075-0,09
Нержавеющие аустенитные стали	600	0,25-0,33	4,7-4,8	0,053-0,07
Медь	400	3,7-3,8	3,85-4,0	0,95-0,.96
Латунь	350-400	1,17	3,45	0,34
Технический титан	700	0,17	2,8	0,06

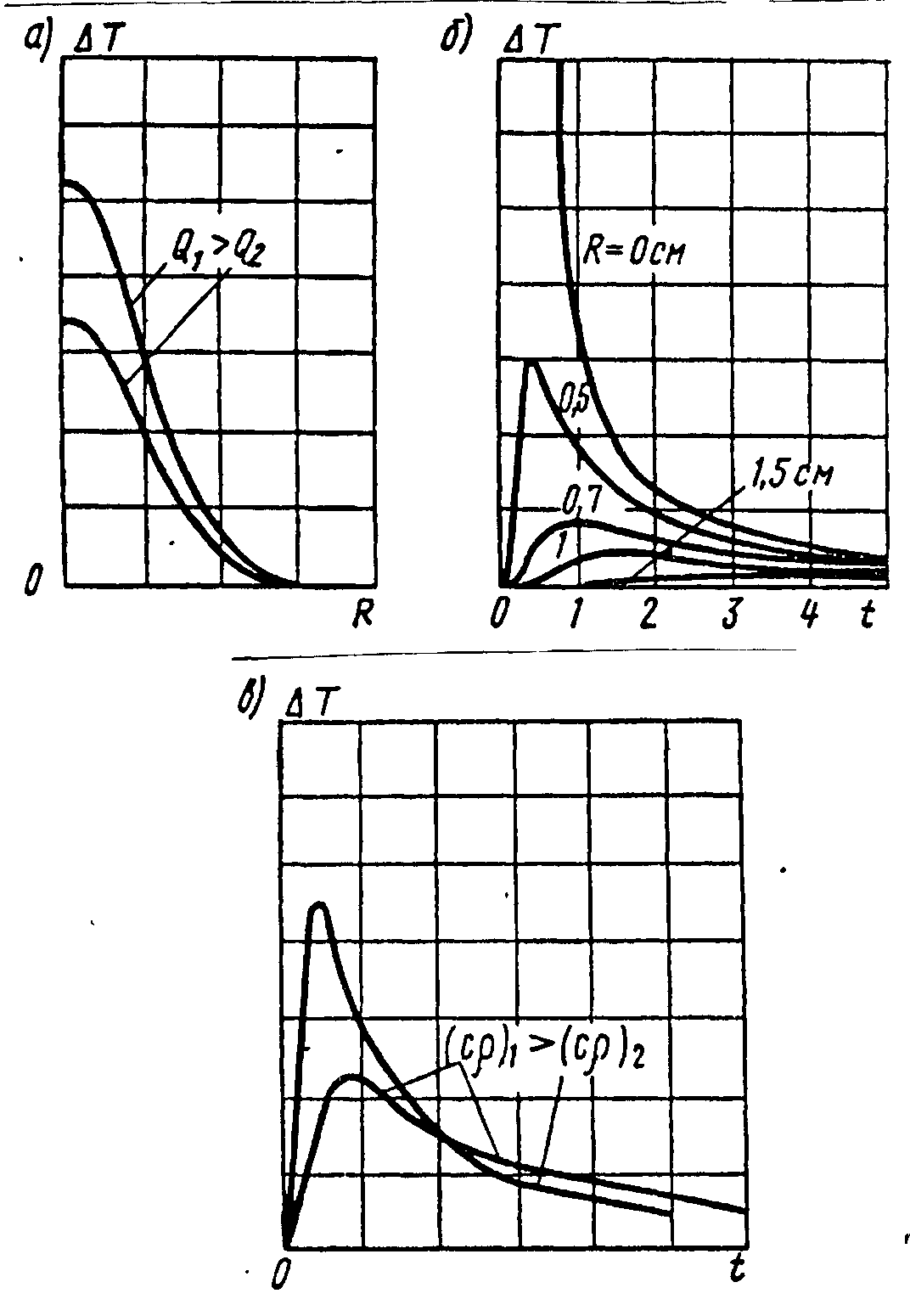
Рис. 1 Зависимость приращения температур мгновенного точечного источника в полубесконечном теле от:

а – количества введенной теплоты

б – расстояния до точки О

в – теплоемкости материала с_р

Мгновенные сосредоточенные источники теплоты.

При лазерной обработке сфокусированным излучением в виде отдельного импульса или непрерывного воздействия в течение короткого промежутка времени на поверхности тела можно воспользоваться формулой для мгновенного сосредоточенного источника. Процесс распространения тепла мгновенного сосредоточенного источника Q, выделившегося на поверхности полубесконечного тела в начальный момент времени t =0 в точке 0 (мгновенный точечный источник) выражается уравнением

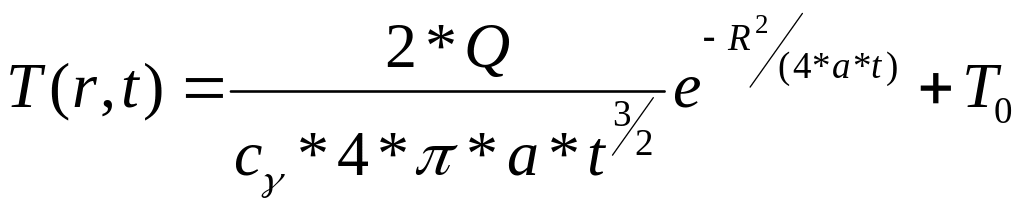(1)

где: Т – температура в рассматриваемой точке с координатами x, y, z;

t – время отсчитываемое с момента введения теплоты;

R²=x²+y²+z² – квадрат расстояния от источника тепла Q до рассматриваемой точки тела с координатами x, y, z;

а = λ_t / с_γ – коэффициент температуропроводности;

Т₀ – температура окружающей среды, то есть начальная температура материала перед лазерной обработкой (в последующих формулах условно принимается Т₀ = 0).

Теплоотдача с поверхности х о у не учитывается, так как ее влияние на тепловые процессы в полубесконечном теле несравненно меньше, по сравнению с распространением тепла в теле путем теплопроводности.

Из формулы (1) следует, что температура точек тела в любой момент времени t прямо пропорциональна количеству введенного тепла (рис.1а).

Характер изменения температуры в точках на различных расстояниях R от точки О одинаковый – повышение температуры на начальной стадии, достижение максимальных значений и последующее уменьшение (рис.1б). При этом в более удаленных точках максимальная температура имеет меньшее значение и достигается позже. В точке О, где приложен мгновенный источник тепла, в начальный момент времени t = 0 расчетная температура стремится к бесконечности. Температуры всех точек полубесконечного тела с течением времени стремятся к нулю.

В материале, имеющем большее значение коэффициента λ_t при постоянной теплоемкости с_γ , распределение теплоты происходит интенсивнее. При этом максимальные значения температур в различных точках остаются одинаковыми, но в материале с большей теплопроводностью максимальные температуры достигаются быстрее.

Изменение теплоемкости с_γ при постоянной теплопроводности λ_t неоднозначно влияет на процесс распространения теплоты. Это наглядно видно из сопоставления изменения температуры во времени в одной и той же точке тела при различных значениях теплоемкости с_γ (рис. 1в).