Вариант 6
1. В
цирке медведь должен прокатиться на
самокате по арене, не падая, три круга.
Случайная величина X
– число кругов, пройденных без падения.
Вероятность упасть 0,4. Найти M(X);
D(X);
p(1 < X < 3).
2. Задана плотность распределения случайной величины X:
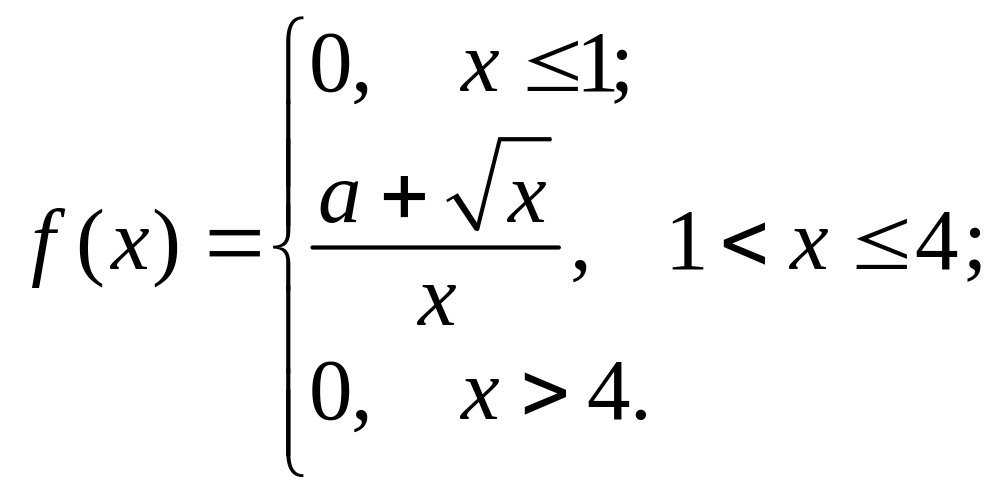
Найти
.
3. На бурение одной нефтяной скважины уходит 5 часов работы. Найти вероятность того, что инженер, приехавший к месту бурения, будет ждать конца работы менее 1 часа, среднее и среднеквадратическое времени ожидания.
4. Вероятность того, что оперативное запоминающее устройство (ОЗУ), купленное в магазине «Клондайк», проработает без поломки от 1 до 1,5 года, равна 0,8. Найти вероятность того, что это ОЗУ проработает без поломки от 2 до 3 лет.
5. Химический завод выпускает керосин номинальной плотности 0,80 кг/м3. В результате статических испытаний обнаружено, что практически 98,08% всего выпускаемого керосина имеет плотность в интервале (0,77; 0,83). Закон распределения плотности близок к нормальному. Найти вероятность того, что керосин удовлетворяет стандарту, если для этого достаточно, чтобы его плотность не отклонялась от номинала более чем на 0,02 кг/м3.
6. Случайная
величина
имеет показательное распределение.
Задана вероятность
.
Найти математическое ожидание и дисперсию
случайной величины
.
7. Индикатор
круглого обзора навигационной станции
представляет собой круг радиуса
.
Вследствие помех может появиться пятно
с центром в любой точке этого круга.
Определить математическое ожидание и
дисперсию расстояния центра пятна от
центра круга.
8. Случайная
величина X
распределена по нормальному закону с
параметрами
.
Найти плотность распределения случайной
величины Y,
если
.
Вариант 7
1.
Охотник стреляет по дичи до первого
попадания, но успевает сделать не более
четырёх выстрелов. Составить закон
распределения X
– числа промахов, если вероятность
попадания в цель при одном выстреле
равна 0,6. Определить M(X),
D(X),
F(x).
2. Непрерывная случайная величина X задана функцией распределения:
F(x)
=
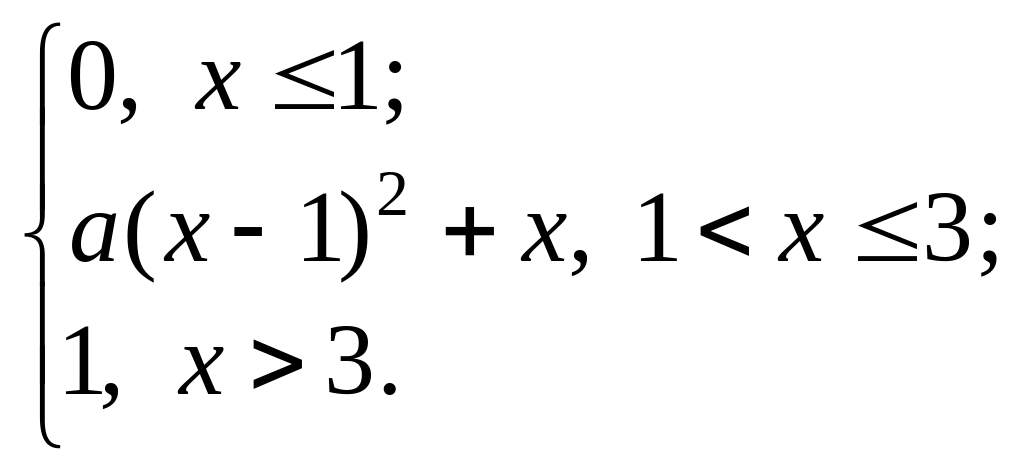
Найти
a,
M(X),
D(X),
,
f(x).
3. Цена деления шкалы измерительного прибора равна 0,4. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчёте будет сделана ошибка: a) меньшая 0,06; б) бόльшая 0,05.
4. Непрерывная
случайная величина X
распределена по показательному закону,
заданному плотностью вероятности
f(x) = 4е−4x
при x
0.
Найти вероятность того, что в результате
испытания X
попадает в интервал (0,2). Определить
M(X),
D(X),
F(x).
5. Пусть вес пойманной рыбы подчиняется нормальному закону распределения с параметрами а = 450 г, = 20 г. Найти вероятность, что вес одной пойманной рыбы будет: а) от 370 до 420 г; б) не более 530 г; в) больше 300 г.
6. Случайные величины X и Y независимы. Найти D(2X + 3Y), D(3X – 2Y), если известно, что D(X) = 5, D(Y) = 3.
7. Закон распределения системы двух дискретных случайных величин задан таблицей:
Y |
X |
|||
–0,5 |
0 |
1 |
2 |
|
1 |
0,1 |
0,15 |
0,2 |
0,05 |
2 |
0,25 |
0,1 |
0 |
0,15 |
Найти:
а) законы распределения X
и Y;
б) М(X)
и М(Y);
в) условные законы распределения
;
.
8. Светящаяся точка, изображающая наблюдаемый объект на круглом экране радиолокатора, может случайным образом занимать любое положение на экране (плотность вероятности постоянна). Диаметр экрана равен D. Найти математическое ожидание расстояния R от светящейся точки до центра экрана.