Приложение 4
Варианты контрольного задания № 2 Вариант 1
1.
Случайная величина Х
распределена по закону p(X = к) =
= с4к–1,
Найти коэффициент с,
F(x),
M(X),
D(X),
2. Непрерывная случайная величина X задана функцией распределения:
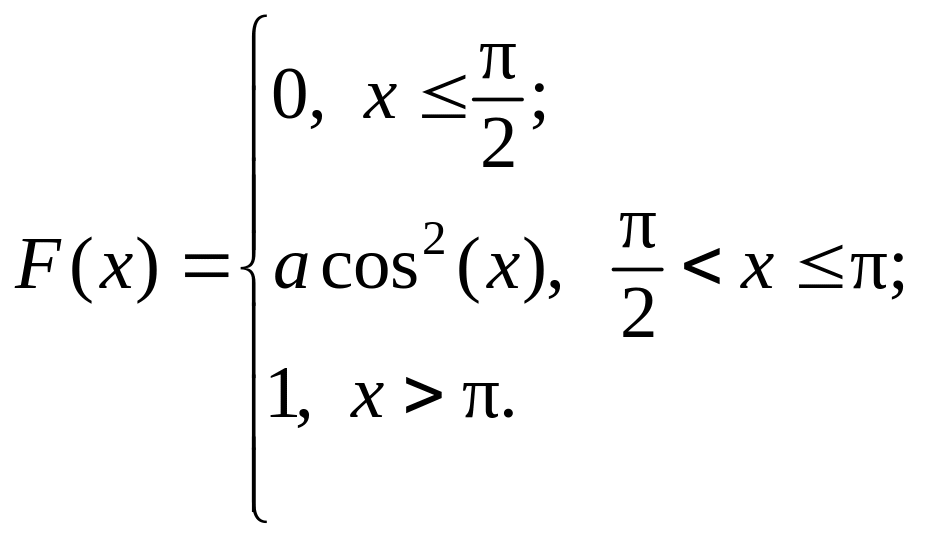
Найти
а,
M(X),
D(X),
,
.
3. Цена деления шкалы измерительного прибора равна 0,1. Показания прибора округляют до ближайшего целого деления. Найти вероятность того, что при отсчете будет сделана ошибка, большая 0,04.
4. Гарантия на купленные в магазине часы 1 год. Среднее время работы без поломок этих часов – 2 года. Найти вероятность того, что часы не придется возвращать в магазин по гарантии.
5.
Полагая, что возраст населения страны
подчиняется нормальному закону
распределения с параметрами
найти долю мужчин в возрасте от 25 до 35
лет. При расчете учитывать, что на 10
женщин приходится 9 мужчин.
6. Найти математическое ожидание и дисперсию суммы числа очков, которые могут выпасть при бросании двух игральных костей.
7. Система случайных величин задана плотностью распределения:
где
D
= {треугольник:
}.
Найти а,
,
8.
Случайная величина Х
распределена равномерно в интервале
.
Найти плотность распределения случайной
величины
Вариант 2
1. Игральная кость бросается 3 раза. Написать ряд распределения случайной величины Х – числа выпадения единицы. Найти F(x), M(X), D(X), .
2. Непрерывная случайная величина X задана плотностью распределения:
Найти а, F(x), M(X), D(X), .
3.
Случайная величина X
распределена по равномерному закону
на интервале (
).
Найти t1
и t2,
если M(X) = 6,
.
Записать выражение
4. Время ожидания у бензоколонки автозаправочной станции является случайной величиной Х, распределённой по показательному закону со средним временем ожидания, равным 2 минутам. Найти вероятность того, что ждать придется не более 1 минуты.
5.
Производится измерение диаметра
отверстия втулки без систематических
ошибок. Случайные ошибки измерения Х
подчинены нормальному закону со средним
квадратичным отклонением
мм. Найти вероятность того, что измерение
будет произведено с ошибкой, не
превосходящей по абсолютной величине
15 мм.
6. Каждый из трех гимнастов выполнил заданное упражнение по одному разу. Вероятности успешного выполнения упражнения 0,7; 0,8; 0,9 соответственно. Найти математическое ожидание и дисперсию случайной величины Х – количества правильно выполненных упражнений.
7. Задана функция распределения двумерной случайной величины
Найти
вероятность попадания случайной точки
(Х,
Y)
в прямоугольник, ограниченный прямыми:
x
= 0, x =
,
y
=
,
y
=
и
8. Заданы законы распределения случайных величин Х и Y
X |
0 |
1 |
3 |
; |
Y |
1 |
2 |
4
. |
p |
0,1 |
0,5 |
0,4 |
p |
0,6 |
0,3 |
0,1 |
Найти
закон распределения
Вариант 3
1. Случайная
величина Х
распределена по закону p(X = к) =
= с(к + 2к),
Найти коэффициент с,
F(x),
M(X),
D(X),
.