3.2 Короткі теоретичні відомості

Рішенням прямої задачі гравіметрії для тіл правильної геометричної форми є визначення гравітаційного ефекту від даних об’єктів. Якщо на досліджуваній ділянці на певній глибині знаходиться карстова порожнина, то за допомогою методу гравіметрії можна її оконтурити. А у випадку проведення режимних спостережень можна зробити висновок про інтенсивність розвитку карсту і навіть передбачити місця можливих провалів.

Для прикладу розглянемо рішення прямої задачі гравіметрії для елементарного тіла – кулі. Аномалію для профіля, що проходить через центр кулі, можна визначити за фор-мулою

(м/с²), (3.1)

де - надлишкова маса кулі, що визначається за формулою

(кг), (3.2)

- об’єм кулі ( ) (м³);

- різниця щільності між оточуючими порода-ми та породами об’єкту (кулі) (кг/м³); - радіус кулі (м); - глибина залягання центра кулі (м); - координата по профілю (м); (м³/кг·с²) – гравітаційна стала.

Крива над кулею має вигляд, що показано на рис.3.1.

Обернена задача гравіметрії - це знаходження глибини залягання об’єкта, його розмірів та надлишкової маси. Глибина центра кулі знаходиться з рівності

, (3.3)

де - значення абсциси при половині максимуму .

0

X

Х₁

h

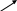
R

Рисунок 3.1 – Крива над кулею

Надлишкова маса визначається за відомим значення та максимальним значенням , що знімається з побудованого графіка (див. рис. 4.1):

. (3.4)

Якщо відома надлишкова густина даного об’єкта, то можна знайти його радіус за формулою

, (3.5)

де - різниця щільності між оточуючими породами та геологічним об’єктом.

3.3 Порядок виконання роботи

1 Розрахувати гравітаційне поле, що обумовлене елементар-ним тілом (кулею), використовуючи формули (3.1) та (3.2). Розрахунки можна виконувати на ПЕОМ або за допомогою мікрокалькулятора.

2 При розрахунках використовувати такі дані:

R=100+5(n-1) (м), де n – номер студента по списку групи;

h=400 (м); 2300 (кг/м³); 2000 кг/м³;

змінюється від –1000 до +1000 (м) з кроком 100 (м).

3 За виконаними розрахунками побудувати криві над кулею з різними значеннями , тобто та (на одному рисунку).

4 Для одного з графіків вирішити обернену задачу, тобто знайти радіус кулі, надлишкову масу та глибину залягання. Порівняти отримані значення з вхідними даними.

5 Звіт по роботі повинен містити:

- завдання на виконання лабораторної роботи;

- вихідні дані для свого варіанту;

- формули розрахунку та результати обчислень;

- побудовані графіки та висновок про їх взаємне розташування.