Тесты самоконтроля знаний (преобразование комплексного чертежа)

1 Как называется линия А₁А₂?

1. проекционная линия

2. ось проекций

3. вертикальная линия связи

4. горизонтальная линия связи

Ответ:

2 Как называется точка проекции А₄?

1. горизонтальная

2. фронтальная

3. профильная

4. дополнительная Ответ:

3 Какое расстояние нужно измерить для построения проекции А₄?

1. Е

2. h

3. f

4. A₂A₃

Ответ:

4 Правильно ли найдена действительная величина треугольника АВС?

1) да

2) нет

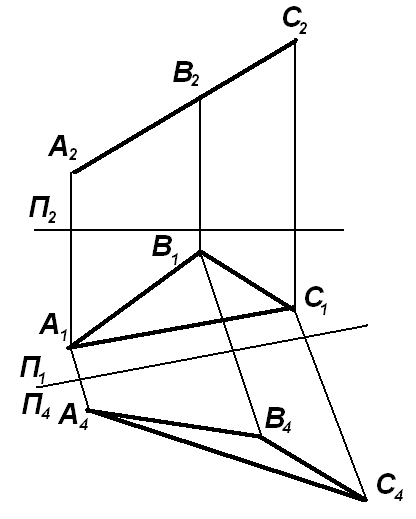
Ответ:

5 Каким способом определена величина отрезка АВ прямой?

1. замена плоскостей проекций

2. способ прямоугольного треугольника

3. способ плоскопараллельного движения

4. способ вращения вокруг следа плоскости

Ответ:

6 Какая плоскость проекции заменена?

1) П₁

2) П₂

3) П₃

Ответ:

7 Тема 5 многогранные поверхности. Взаимное пересечение поверхностей Вопросы самоконтроля:

1. Чем определяется принадлежность точки поверхности многогранника?

2. Что представляет собой фигура сечения многогранника плоскостью?

3. Какими способами можно решить задачу о пересечении многогранника плоскостью?

4. Запишите алгоритм решения задачи о построении точек пересечения прямой линии с поверхностью многогранника.

5. Какова последовательность действий (алгоритм) при решении задачи на пересечение поверхностей?

7. В чем сущность метода вспомогательных секущих плоскостей - посредников?

УПРАЖНЕНИЯ

7.1 Построить проекции и определить видимость ребер и граней пирамиды. S - вершина, АВСD - основание. Достроить фронтальную проекцию точки Е, принадлежащей грани SАВ.

7.2 Построить проекции сечения пирамиды SАВС плоскостью ).

7.3 Построить точки пересечения прямой l с поверхностью призмы АВС.

ЗАДАЧИ

7.4 Построить проекции сечения пирамиды SАВС плоскостью (КLМ). Для решения можно воспользоваться способом преобразования чертежа.

7.5 Построить проекции сечения призмы АВС А'В'С' плоскостью S(МNР).

7.6 Построить проекции сечения пирамиды SАВС плоскостью (МNР).

7.7 Построить проекции линии пересечения конуса вращения с гранями проецирующей призмы.

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ:

Задача 1 Задана фронтальная проекция точек М(М₂) и N (N₂) на видимых гранях поверхности.

Решение:

Так как каждая грань – это плоскость, ограниченная многоугольником, для грани действуют все признаки инцидентности, определенные для плоскости.

Рисунок -7.1

Для построения горизонтальной проекции точки М₁ нужно в грани построить любую прямую, проходящую через точку М, тогда соответствующие проекции точки будут лежать на проекциях этой прямой. Удобно использовать прямую, параллельную ребру основания, например (1₂М₂ || (В₂С₂)→(1₁М₁) ||(В₁С₁). Можно также через проекцию N₂ (SBC) и вершину S₂ провести прямую (S₂2 ₂)→(S₁2₁) и по линии связи взять N₁. В призме через N₂ проводим прямую линию (N₂2₂)|| (B₂B¹₂) и на ней по линии связи (N₂N₁) находим N₁. Использование свойства параллельности и заданных вершин сокращает объем работы.

Задача 2 Построить сечение пирамиды плоскостью.