- •Учебное пособие по начертательной геометрии
- •1 Методические указания к решению и оформлению задач
- •2 Принятые обозначения
- •Примеры решения задач:
- •Решение:
- •Тесты самоконтроля знаний (точка)
- •3.2 Комплексный чертеж прямой упражнения
- •Примеры решения задач:
- •Решение:
- •Тесты самоконтроля знаний (плоскость)
- •5 Тема 3 взаимное положение прямых и плоскостей Вопросы самоконтроля:
- •Алгоритм построения точки пересечения:
- •Тесты самоконтроля знаний (взаимное положение прямых и плоскостей)
- •6 Тема 4 способы преобразования чертежа Вопросы самоконтроля:
- •Упражнения
- •Примеры решения задач
- •Решение: Алгоритм графических построений:
- •Решение:
- •Алгоритм графических построений:
- •Тесты самоконтроля знаний (преобразование комплексного чертежа)
- •7 Тема 5 многогранные поверхности. Взаимное пересечение поверхностей Вопросы самоконтроля:
- •Алгоритм графических построений:
- •Тесты самоконтроля знаний (поверхности)
- •БиблиографиЧеский список
Примеры решения задач:
Задача 1 Плоскость общего положения задана треугольником АВС.
Построить горизонталь плоскости и линию ската.

Решение:
Горизонталь параллельна плоскости П 1 а это значит, что её проекция на П 2 будет горизонтальной линией. В любом месте начертим эту проекцию. В любом потому, что горизонталей у плоскости бесконечное количество и нам не имеет значения, какую из них строить. Найдем точки пересечения K2 и L2 со сторонами АВС. Опустив линии связи, находим проекции K1 и L1 горизонтали. Прямая, принадлежащая плоскости и перпендикулярная к горизонтали называется линией ската. На основании свойства проецирования прямого угла М1N1 перпендикулярна K1L1. М N и есть линия ската.
Тесты самоконтроля знаний (плоскость)
1 В каком случае прямая принадлежит плоскости?
если хотя бы одна точка прямой принадлежит плоскости
если две точки прямой принадлежат плоскости
если три точки прямой принадлежат плоскости. Ответ:
2 Как расположена линия наибольшего наклона плоскости общего положения?
║ горизонтали плоскости
┴ горизонтали плоскости
пересекаются с горизонталью Ответ:
3 Точка К, принадлежащая заданной плоскости, изображена на рисунке:
|
|
|
Ответ:
4 Проецирующая плоскость изображена на рисунке:
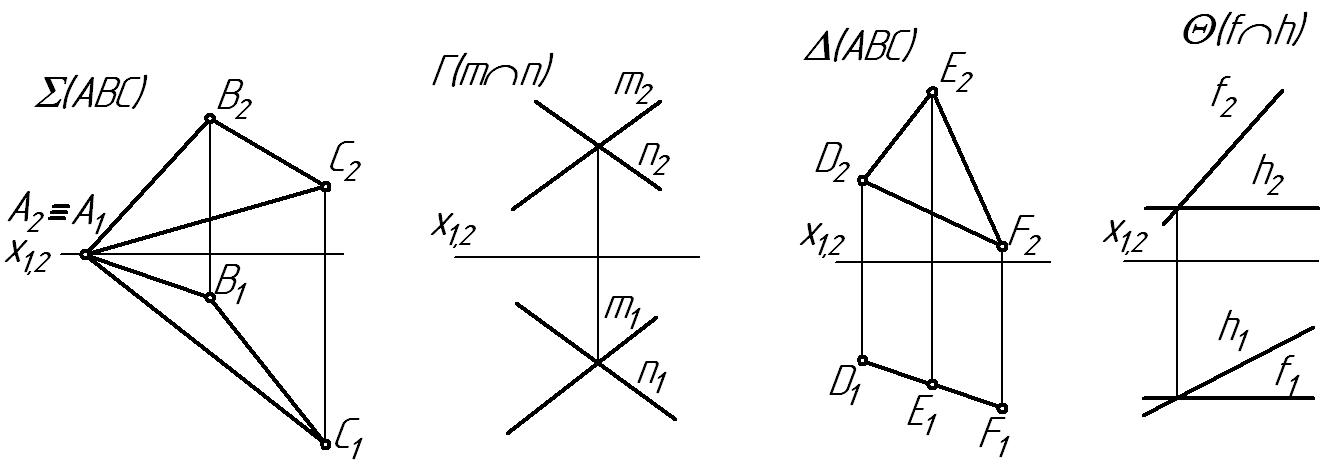
1) 2) 3) 4) Ответ:
5 Плоскость уровня изображена на рисунке:
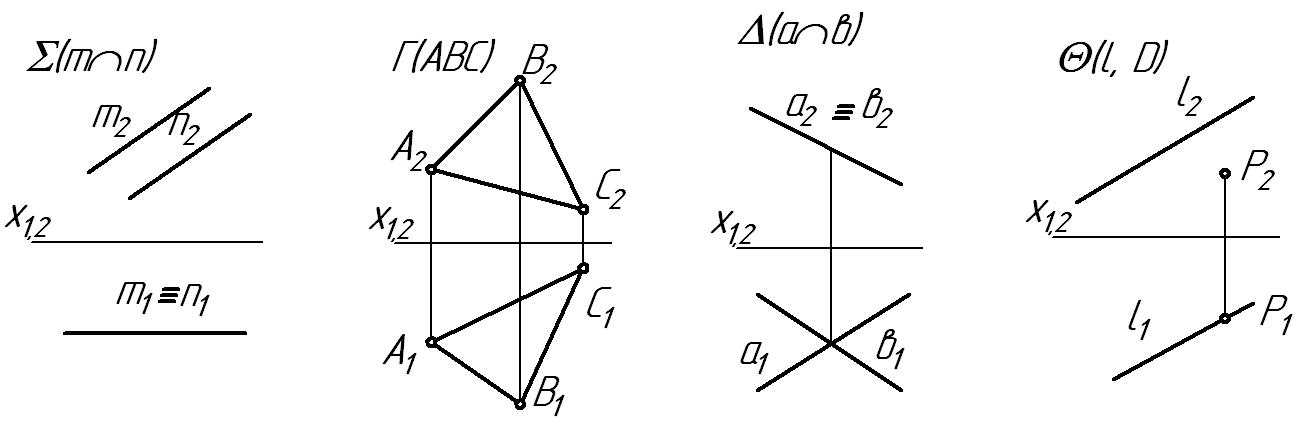
1) 2) 3) 4) Ответ:
6 Плоскость общего положения изображена на рисунке:
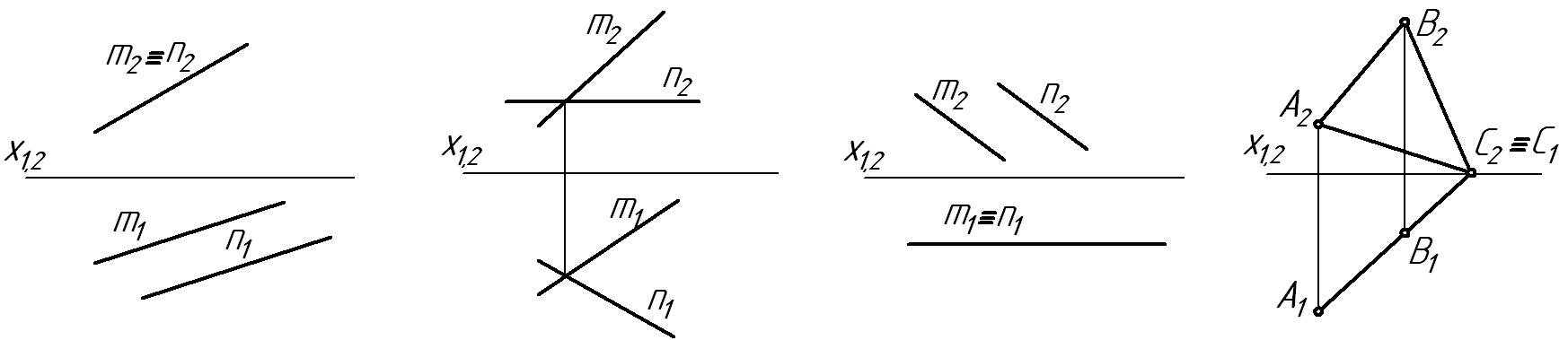
1) 2) 3) 4) Ответ:
7 Н а каком чертеже имеется изображение Δ АВС в натуральную величину?

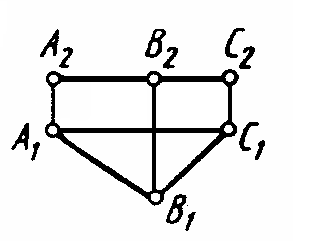

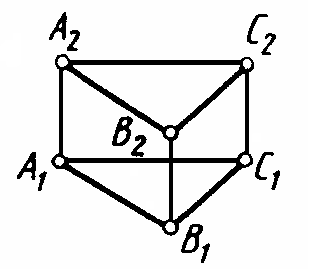
Ответ:
8 Как называется плоскость проекции П2
дополнительная 2)горизонтальная 3) фронтальная 4) профильная Ответ:
4.2 Перпендикулярность прямых и плоскостей
Вопросы самоконтроля:
1 Сформулируйте условие перпендикулярности прямой и плоскости в пространстве и на комплексном чертеже. Кратко запишите это условие.
2 Сформулируйте условие перпендикулярности двух плоскостей в пространстве и на комплексном чертеже. Кратко запишите это условие.
УПРАЖНЕНИЯ
4.2.1 Построить в
точке А перпендикуляр к плоскости ∑ (m
![]() n)
и отложите на нем отрезок l.
n)
и отложите на нем отрезок l.

4.2.2 Построить плоскость σ, проходящую через точку С и перпендикулярную прямой АВ общего положения.

ЗАДАЧИ
4.2.3 Из точки А восстановить перпендикуляр к плоскости АВС и отложите на нем отрезок длиной m. Составить алгоритм решения задачи.

4.2.4 Определить расстояние от точек С и D до прямой h.

Через точку М провести плоскость, перпендикулярную к двум данным плоскостям P(aIIb) и Q(ABC).

ПРИМЕРЫ РЕШЕНИЯ ЗАДАЧ:
Задача 1 Построить проекции перпендикуляра m, опущенного из точки D на плоскость σ (АВС).
Решение:
Строим в плоскости σ (АВС) проекции фронтали f (f1, f2) и горизонтали h (h1, h2).
Проводим m1 перпендикулярно h1, причем D1€ m1.
Проводим m2 перпендикулярно f2, причем D2€ m2.
Прямая m (m1, m2) - искомый перпендикуляр, так как она перпендикулярна двум пересекающимся прямым плоскости σ (АВС)= h∩f.

ТЕСТЫ САМОКОНТРОЛЯ ЗНАНИЙ
(ПЕРПЕНДИКУЛЯРНОСТЬ ПРЯМЫХ И ПЛОСКОСТЕЙ
1 Прямая d, перпендикулярная плоскости Р (m∩n), изображена на чертеже:
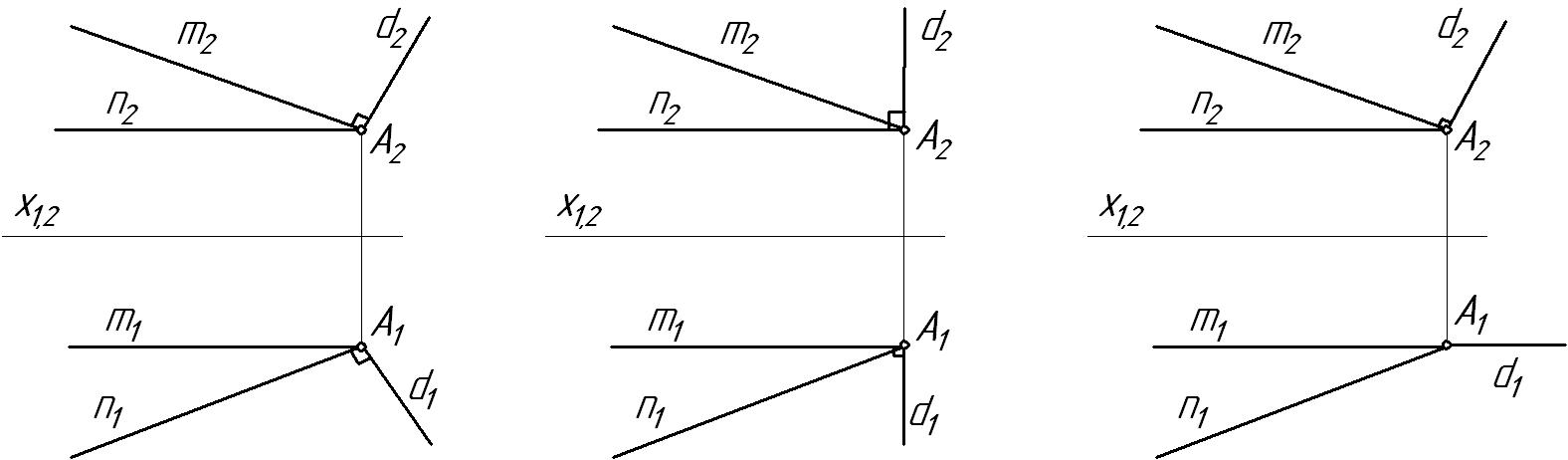
1) 2) 3) Ответ:
2 Плоскость Р (c∩d), перпендикулярная прямой m, изображена на рисунке:
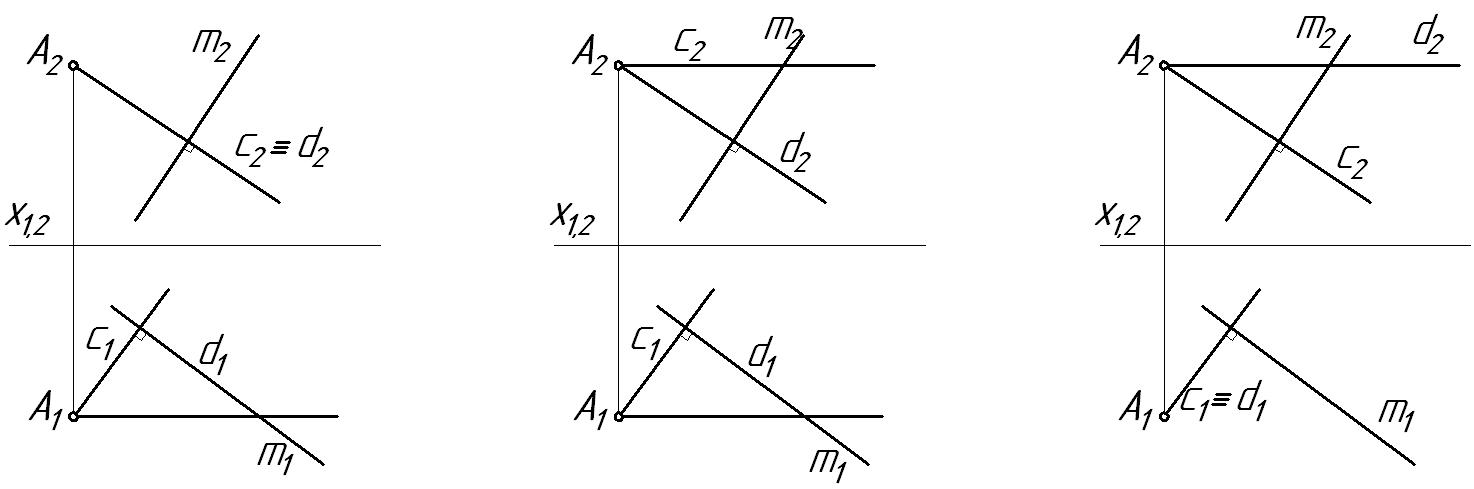

1) 2) 3) Ответ:
Отрезок МК, перпендикулярный плоскости треугольника АВС, изображен на чертеже:
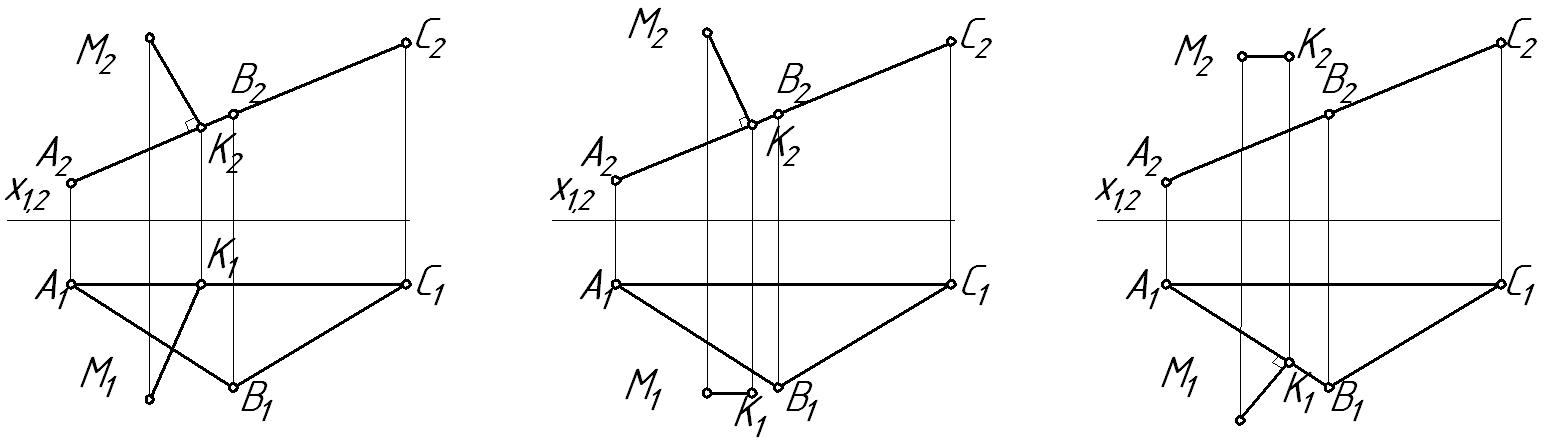
1) 2) 3) Ответ:
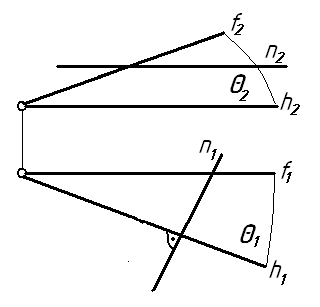
4 На каком чертеже прямая n перпендикулярна плоскости θ (h∩f)? Ответ:
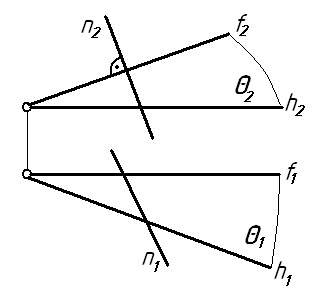
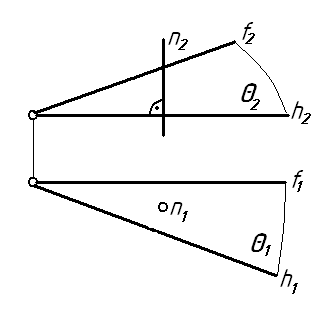
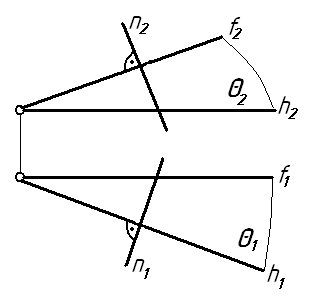
5 На каком чертеже заданы проекции двух взаимно перпендикулярных плоскостей?
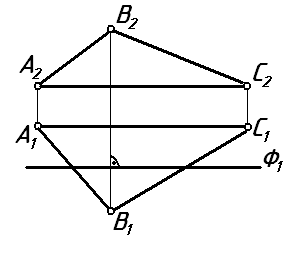
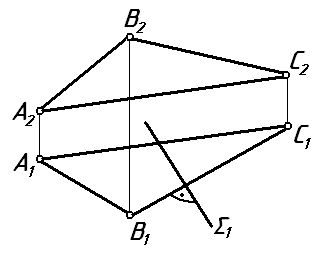
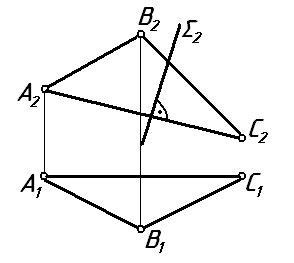
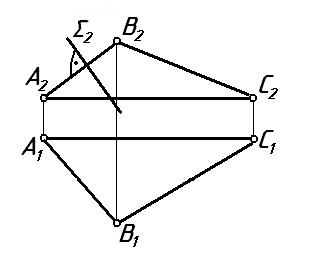
Ответ:
6 Каково условие перпендикулярности прямой ℓ к плоскости ∑.
1) ℓ1 ┴ h1 (∑) 2) ℓ1 ┴ f1 (∑) 3) ℓ1 ┴ h1 (∑)
ℓ2 ┴ f2 (∑) ℓ2 ┴ h2 (∑) ℓ2 ║ f2 (∑) Ответ: