Упражнения

5.1.1 Построить горизонтальную проекцию прямой m, скрещивающейся с линией n. Построить конкурирующие точки, определить видимость.

5.1.3 Построить линию пересечения двух плоскостей α (АВС) и θ.

5.1.2 Построить точку пересечения прямой l с плоскостью α. Определить видимость прямой. а) α (АВС); б) α (m || n)

Задачи

5.2.1 Построить точку К пересечения с плоскостью Θ (CD||EF). Определить видимость прямой, относительно плоскости.

5.2.2 Построить линию пересечения двух плоскостей β (ABC) и α(m||n). Определить видимость плоскостей относительно друг друга.

5.2.3 Построить линию пересечения плоскостей (ABC) и (DEF). Определить видимость.

5.2.4 Построить линию пересечения плоскостей

5.2.5 Построить линию пересечения двух плоскостей

5.2 6 Построить точку К(К1, К2) пересечения прямой АВ с заданной плоскостью. Определите видимость прямой.

Примеры решения задач:

Задача 1 Построить точку М пересечения прямой l с плоскостью α. Определить видимость прямой.

Решение: Рассмотрим алгоритм решения задачи:

На рисунке 3.5а показано решение задачи с помощью горизонтально проецирующего посредника.

1. l⊂ - возьмем П ₁ и l₁ =₁ ;

2. m(1-2)=a∩ - возьмем 1₁ =(А₁ В₁ )∩ ₁ →1₂ ; 2 ₁ =(В₁ С₁ )∩ ₁→2 ₂ ;

3. M= l∩ m-(1₂ -2₂ ) m₂ ∩l ₂ = M₂ →M₁

Для определения видимости на горизонтальной проекции использованы конкурирующие точки 1 (АВ) и 3 l, у которых 1₁ =3₁ . Сравнивая положение проекций 1₁ и 3₁, видим, что точка 3 лежит выше, следовательно, при взгляде сверху мы будем видеть ее, то есть будем видеть прямую l(l₁) до точки М(М₁). Для определения видимости на фронтальной проекции использованы фронтально конкурирующие точки 4 (АС) и 5 l, у которых 4₂ =5_2, но глубина точки 5(5₁) больше, то есть она ближе к наблюдателю, и, следовательно, будет видна прямая линия l₁ 5.

На рисунке 3.5б показано решение этой же задачи с помощью фронтально проецирующего посредника.

Рисунок 3.5

Тесты самоконтроля знаний (взаимное положение прямых и плоскостей)

1 Заданные точки, являющиеся конкурирующими относительно плоскости П₂, изображены на рисунке:

1) 2) 3) 4) Ответ:

2 Параллельные прямые изображены на рисунке:

1) 2) 3) 4) Ответ:

3 На каком чертеже правильно построена точка К пересечения прямой ℓ с плоскостью АВС и показана видимость прямой?

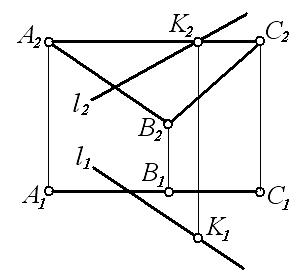
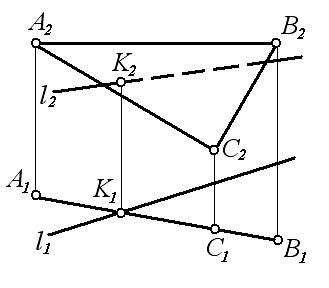
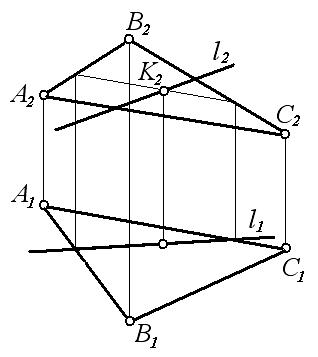
Ответ:

4 Прямая l, принадлежащая плоскости треугольника АВС, изображена на рисунке:

1) 2) 3) Ответ:

5 Взаимно параллельные плоскости изображены на рисунке:

1) 2) 3) Ответ:

6 Тема 4 Параллельность и перпендикулярность прямых и плоскостей Вопросы самоконтроля

1. Сформулируйте условие параллельности двух прямых в пространстве и на комплексном чертеже.

2. Сформулируйте условие параллельности прямой и плоскости в пространстве и на комплексном чертеже. Как построить прямую, параллельную данной плоскости?

3. Сформулируйте условие параллельности двух плоскостей в пространстве и на комплексном чертеже.

4. В чем сущность теоремы о проецировании прямого угла?

5. Сформулируйте условие перпендикулярности прямой и плоскости в пространстве и на комплексном чертеже. Кратко запишите это условие.

6. Сформулируйте условие перпендикулярности двух плоскостей в пространстве и на комплексном чертеже. Кратко запишите это условие.