Зачет по геометрии 11 класс Карточка 1

1. Расскажите, как задаётся прямоугольная система координат в пространстве и как определяются координаты вектора. если через точку пространства проведены три попарно перпендикулярные прямые, на каждой из них выбрано направление и выбрана единица измерения отрезков, то задается прямоугольная система координат)

2. Выведите формулы, выражающие координаты точки пересечения медиан треугольника через координаты его вершин. Пусть координаты таковы: A(x1;y1), B(x2;y2), C(x3;y3) AM, BN - медианы треугольника, O - точка пересечения медиан. Так как M - середина BC, то ее координаты: M((x2+x3)/2;(y2+y3)/2) Находим координаты вектора AM AM = ((x2+x3)/2-x1;(y2+y3)/2-y1) AM = ((x2+x3-2x1)/2;(y2+y3-2y1)/2) Дальше используем свойство, что медианы точкой пересечения делятся в отношении 2 к 1, считая от вершины, то есть AO = 2 * OM, Тогда AO = 2/3 * AM Значит вектора AO AO = (2/3 * (x2+x3-2x1)/2;2/3 * (y2+y3-2y1)/2) AO = ((x2+x3-2x1)/3;(y2+y3-2y1)/3) Осталось найти координаты точки O(x0;y0) AO = (x0 - x1; y0 - y1) Значит x0 - x1 = (x2 + x3 - 2 * x1)/3 => x0 = (x1 + x2 + x3)/3 y0 - y1 = (y2 + y3 - 2 * y1)/3 => y0 = (y1 + y2 + y3)/3

3. Дан куб ABCDA₁B₁C₁D₁, точка М – центр грани AA₁D₁D. Вычислите угол между векторами BM и B₁C. Вводите систему координат: начало координат (например) в точке В, ось х - по ребру ВА, ось у - по ребру ВС, ось z - по ребру В1. Ребро куба 1 (или а, роли не играет). Вычисляем координаты вершин куба: B(0,0,0) A(1,0,0) B1(0,0,1) C(0,1,0) D(1,1,1) M(1,1/2,1/2) Далее вычисляете координаты векторов ВМ и В1С и находите скалярное произведение

Карточка 2

1. Расскажите о связи между координатами векторов и координатами точек.

координаты вектора - это разность координат его конца и координат его начала.

2. Выведите формулы, выражающие координаты середины отрезка через координаты его концов. x1, Y1 - координаты одного конца отрезка  x2, Y2 - координаты второго конца отрезка  x3, Y3 - координаты середины отрезка  x3=(x1+x2)/2  Y3=(y1+y2)/2 

3. Вычислите угол между прямыми AB CD, если A(1;1;0), B(3;1;0), C(4;-1;2), D(0;1;0). Вычислите координаты и длины векторов АВ и СD, а затем вычислите их скалярное произведение через координаты. Как известно, скалярное произведение двух векторов равно:  (AB, CD) = |AB|*|CD|*cos(AB^CD)  Подставив в эту формулу величину скалярного произведения и длины векторов найдете косинус угла между векторами, а, соответственно и сам угол.  Успехов!

Карточка 3

1. Сформулируйте определение скалярного произведения двух векторов. Определение: Скалярным произведением двух векторов   и 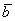  называется ЧИСЛО, равное произведению длин этих векторов на косинус угла между ними: 1.2. Сформулируйте условие перпендикулярности двух ненулевых векторов, используя скалярное произведение.

Скалярным произведением двух ненулевых векторов a и b называется число (скаляр), равный произведению длин этих векторов на косинус угла φ между ними. Скалярное произведение можно обозначать различными способами, например, как ab, a · b, (a , b), (a · b). Таким образом, скалярное произведение равно:

a · b = |a| · |b| · cos φ

Если хотя бы один из векторов равен нулю, то скалярное произведение равно нулю.

2. Выведите формулу для вычисления длины вектора по его координатам. Длину вектора   будем обозначать 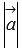 . Из-за такого обозначения длину вектора часто называют модулем вектора.

Начнем с нахождения длины вектора на плоскости по координатам.

Введем на плоскости прямоугольную декартову систему координат Oxy. Пусть в ней задан вектор   и он имеет координаты  . Получим формулу, позволяющую находить длину вектора   через координаты   и  .

Отложим от начала координат (от точки О) вектор  . Обозначим проекции точки А на координатные оси как   и   соответственно и рассмотрим прямоугольник   с диагональю ОА.

В силу теоремы Пифагора справедливо равенство  , откуда  . Из определения координат вектора в прямоугольной системе координатмы можем утверждать, что   и  , а по построению длина ОА равна длине вектора  , следовательно,  .

Таким образом, формула для нахождения длины вектора   по его координатам на плоскости имеет вид  .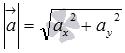

Если вектор   представлен в виде разложения по координатным векторам  , то его длина вычисляется по этой же формуле  , так как в этом случае коэффициенты   и   являются координатами вектора   в заданной системе координат.

Рассмотрим пример.

Пример.

Найдите длину вектора  , заданного в декартовой системе координат.

Решение.

Сразу применяем формулу для нахождения длины вектора по координатам  :

Ответ:

.

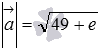Теперь получим формулу для нахождения длины вектора   по его координатам в прямоугольной системе координат Oxyz в пространстве.

Отложим от начала координат вектор   и обозначим проекции точки А на координатные оси как   и  . Тогда мы можем построить на сторонах   и  прямоугольный параллелепипед, в котором ОА будет диагональю.

В этом случае   (так как ОА – диагональ прямоугольного параллелепипеда), откуда  . Определение координат вектора позволяет нам записать равенства  , а длина ОА равна искомой длине вектора, следовательно,  .

Таким образом, длина вектора   в пространстве равна корню квадратному из суммы квадратов его координат, то есть, находится по формуле  .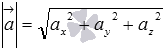

Пример.

Вычислите длину вектора  , где   - орты прямоугольной системы координат.

Решение.

Нам дано разложение вектора   по координатным векторам вида  , следовательно,  . Тогда по формуле нахождения длины вектора по координатам имеем  .

Ответ:

.

3. Даны точки A(0;4;0) B(2;0;0) C(4;0;4) D (2;4;4). Докажите, что ABCD - ромб.

1. Никакого смешанного произведения находить не нужно !  Если две прямые параллельны, то они лежат в одной плоскости. Ибо воистину. 2. Если противоположные стороны в четырехугольнике попарно параллельны и равны, то это параллелограмм , а не обязательно ромб. 3. Для параллелограмм достаточно проверить равенство лишь одной пары противоположных сторон. Итак,  АВ=(2,-4,0), ДС=(2,-4,0), Векторы AB и CD равны, ABCD – параллелограмм. Для того, чтобы показать, что это ромб, ледует еще проверить равенство смежных сторон. ВС=(2,0,4), |AB|^2=2^2+(-4)^2+0^2 |BC|^2=2^2+0^2+4^2 |AB|=|BC| Параллелограмм АBCD ромб