§5. Релятивистский импульс
Рассмотрим две ИСО, одна из которых К`
движется по отношению к системе K:
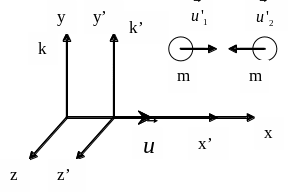
Суммарный импульс этих частиц в системе к` равен 0. В результате абсолютно неупругого удара частицы остановятся в системе к’ и, соответственно, по отношению к системе к будут двигаться вместе с системой к’.
Применив закон сохранения импульса к этому взаимодействию обычным образом, мы обнаружим, что импульс не сохраняется. Однако, если формулу для расчета импульса записать в виде:
,
то закон сохранения импульса будет выполняться. Т.о., записанное выражение представляет собой релятивистский импульс.
Если обозначить:
-
масса покоя, то
,
где
-
релятивистская масса.
Проверим, что выражение для импульса является инвариантом. Скорости:
,
т.к.
( вторая частица в системе к
покоится)
Тогда суммарный импульс р частиц в системе к до соударения равен импульсу первой частицы.
.
Если считать, что в результате соударения образовалась частица массой 2m, то кажется, что закон сохранения импульса не выполняется. На самом деле масса образовавшейся частицы окажется больше, чем сумма масс столкнувшихся частиц, на величину, эквивалентную энергии диссипации.
§6. Энергия частицы в релятивистском случае
II закон Ньютона в
релятивистском случае:
,
где p - релятивистский
импульс.
По теореме о кинетической энергии:
.
Отсюда:
- определенное с точностью до аддитивной
постоянной выражение для
:
очевидно, что эта константа должна быть
выбрана из условия обращения в ноль
при нулевой скорости.
Используя формулу приближенных вычислений
,
можно получить
«привычное» выражение для кинетической
энергии
Итак,
- приближенная формула
для малых скоростей.
Для того, чтобы энергия была инвариантом
по отношению к преобразованию Лоренца,
т.е. чтобы выполнялся закон сохранения
энергии во всех инерциальных системах
отсчета (ИСО), необходимо к кинетической
энергии добавить
:
- полная энергия (инвариант).
- энергия покоя.
Тогда есть разность между полной энергией и энергией покоя.