Л екция 9. Специальная теория относительности.

Введение.

Ньютон считал пространство и время абсолютными во всей вселенной. Однако со времен Галилея известно, что все инерциальные системы отсчета (ИСО) равноправны. Это, в частности, означает, что никакими механическими экспериментами невозможно выявить ту, «главную», систему отсчета, которая была бы неподвижна по отношению к «абсолютному» пространству и вера в существование которой существовала многие столетия. В 19 веке в этом смысле большие надежды возлагались на электродинамику.

В 1860 году был поставлен опыт Майкельсона – Морли по измерению скорости света при распространении света один раз вдоль, а другой раз – против орбитального движения Земли (скорость орбитального движения Земли около 30 км/с). Точность интерферометрических методов измерений позволяла обнаружить различия в скорости света в двух названных случаях. Опыт дал отрицательный результат (в смысле обнаружения неподвижной по отношению к абсолютному пространству системы отсчета): скорость света не зависела от скорости его направления по отношению к скорости орбитального движения Земли.

Спустя почти полвека результат этого опыта был правильно интерпретирован Энштейном, следствием чего стало создание им специальной теории относительности.

§1. Преобразование координат Галилея.

В ньютоновской механике при переходе от одной ИСО K(x,y,z,t) к другой K'(x',y',z',t'), движущейся относительно K поступательно с постоянной скоростью u, пользуются преобразованиями координат, которые называют преобразованиями Галилея.

Выберем оси координат так, чтобы система K' двигалась вдоль положительного направления оси Ох (см. рисунок).

В этом случае преобразования Галилея имеют вид:

и

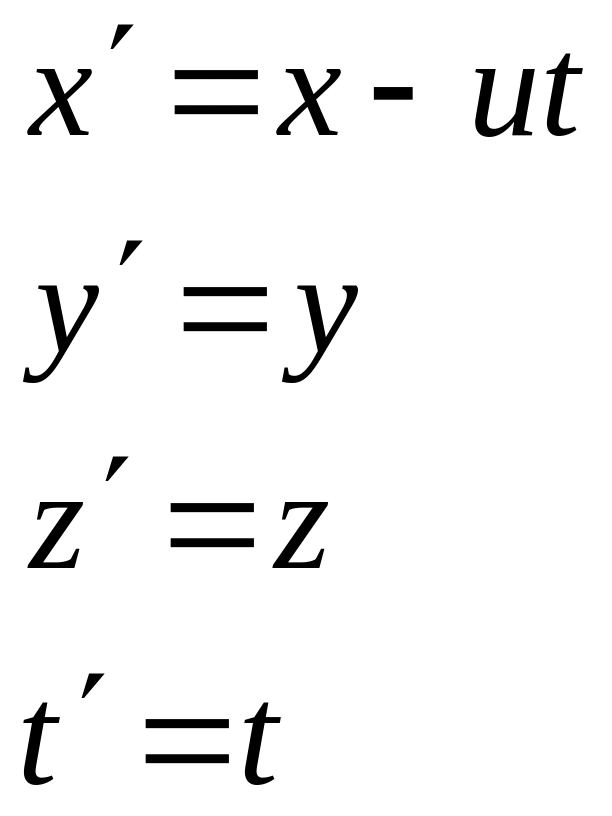
(ход времени не зависит от относительного движения систем отсчета)

Эти формулы называются преобразованиями координат Галилея. Они позволяют переходить от одной ИСО к другой в классической механике.

Продифференцируем эти выражения по времени:

Аналогично:

Тогда можно записать уравнение, которое называется законом сложения скоростей в классической механике:

Продифференцировав по времени, получим

, так как , .

Ускорения оказались равными в обеих системах отсчета, следовательно, уравнения динамики (например, второй закон Ньютона) будут одинаковы во всех инерциальных системах отсчета:

Это обстоятельство позволяет сформулировать механический принцип относительности (принцип относительности Галилея):

Законы механики одинаковы во всех инерциальных системах отсчета.

Или, другими словами,

Уравнения механики инвариантны по отношению к преобразованиям Галилея.

§2. Постулаты теории относительности.

В связи с принципом относительности естественно возникает вопрос: равноправны ли все инерциальные системы отсчета только в механике или также и в отношении других физических явлений и процессов? Нельзя ли выделить из множества инерциальных систем отсчета «главную», основываясь, например, на законах распространения электромагнитных волн? Ответ на этот вопрос был дан в 1905 г. А. Эйнштейном в его работе «К электродинамике движущихся тел», в которой были изложены основные положения специальной теории относительности (СТО). В СТО, так же как и в ньютоновской механике, предполагается, что время однородно, а пространство однородно и изотропно. Специальная теория относительности часто называется также релятивистской механикой, а специфические явления, описываемые этой теорией, - релятивистскими эффектами. В основе СТО лежат постулаты теории относительности Эйнштейна:

1) Все законы природы одинаково формулируются для всех инерциальных систем отсчета.

2) Скорость света в вакууме не зависит от движения источников и приемников света и, следовательно, одинакова во всех инерциальных систем отсчета.