Курсова робота

ПОЯСНЮВАЛЬНА ЗАПИСКА

(позначення документа в разі необхідності)

(тема роботи)

(дисципліна)

Керівник

(підпис, дата, посада, прізвище, ініціали)

Студент

(група, підпис, дата, прізвище, ініціали)

Харків 20

Додаток Г

L

t. j

ПРИКЛАД ВИКОРИСТАННЯ АЛГОРИТМУ ПРИМА ДЛЯ СИНТЕЗУ ТОПОЛОГІЇ МЕРЕЖІ У ВИГЛЯДІ НАЙКОРОТШОГО ДЕРЕВА

Нехай задана деяка множина пунктів мережі і відстані між ними, тобто

	1	2	3	4	5	6	7	8	9	10
1	0	5.5	5.4	8.6	12.7	12.7	11.1	13.4	12.1	19.8
2	5.5	0	7.0	8.0	8.9	7.3	6.4	11.7	11.8	16.7
3	5.4	7.0	0	3.6	9.6	12.6	13.3	8.5	6.7	15.5
4	8.6	8.0	3.6	0	6.8	11.5	13.7	4.9	3.8	12.0
5	12.7	8.9	9.6	6.8	0	7.3	11.8	5.5	8.3	8.0
6	12.7	7.3	12.6	11.5	7.3	0	5.5	12.5	14.4	14.2
7	11.1	6.4	13.3	13.7	11.8	5.5	0	16.3	17.4	19.3
8	13.4	11.7	8.5	4.9	5.5	12.5	16.3	0	3.5	7.4
9	12.1	11.8	6.7	3.8	8.3	14.4	17.4	3.5	0	10.6
10	19.8	16.7	15.5	12.0	8.0	14.2	19.3	7.4	10.6	0

задана матриця L

яка представлена нижче.

Відповідно до алгоритму Прима спочатку виписується перший рядок матриці L без першого стовпця, що відповідає організації зв'язку від першої вершини (центрального пункту) до інших i - х ( i = 2. N ):

2	3	4	5	6	7	8	9	10
5.5	5.4	8.6	12.7	12.7	11.1	13.4	12.1	19.8

Вибираємо в цьому рядку мінімальний елемент L₁₃ = 5.4. Далі

викреслюємо відповідний йому 3-й стовпець матриці L і, рухаючись по 3-му рядку, порівнюємо значення приведених у ній елементів з їх значеннями в першому рядку без першого і 3-го стовпців. Якщо значення елемента 3-го рядка у відповідному стовпці виявляється меншим значення, зазначеного в першому рядку, то ці значення міняються місцями. Якщо найменшим буде значення в першому рядку, то заміна не виконується. У такий спосіб формується наступний рядок:

2	4	5	6	7	8	9	10
5.5	3.6	9.6	12.6	11.1	8.5	6.7	15.5
	(3)	(3)	(3)		(3)	(3)	(3)

При цьому цифрою 3 у дужках позначені ті значення довжин, що взяті з третього рядка.

Знову вибираємо мінімальний елемент рядка L_{4 3} = 3.6. Діючи аналогічно попередньому, одержуємо новий рядок: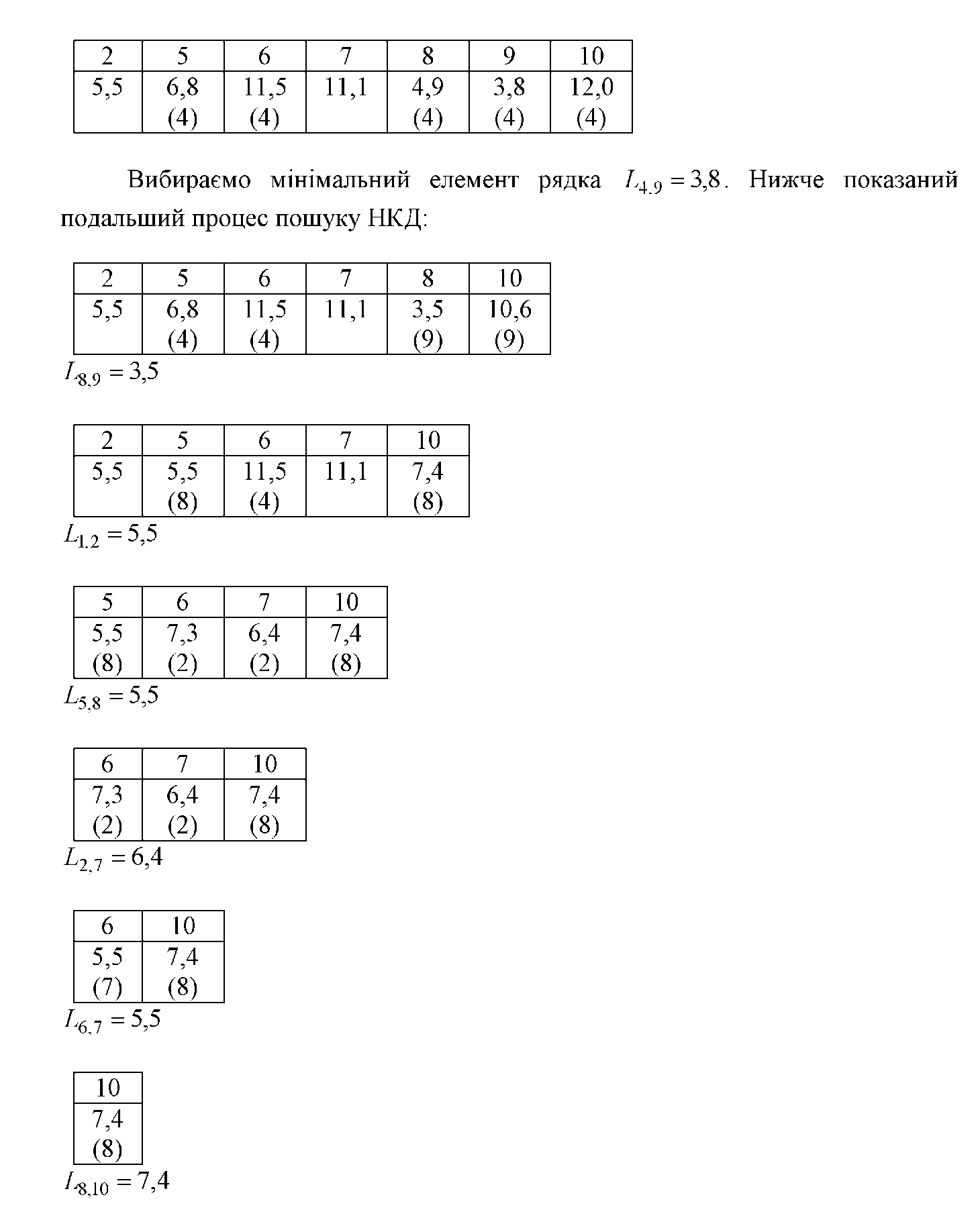

Отже, НКД буде містити ребра L₁₃, L_{3 4}, L_{4 9} L_{8 9}, L₁₂, L_{5 8}, L_{2 7}, L_{6 7} і L₈₁₀ загальною довжиною 46,6 одиниць.Топологія такої мережі представлена на рис. Г.1.

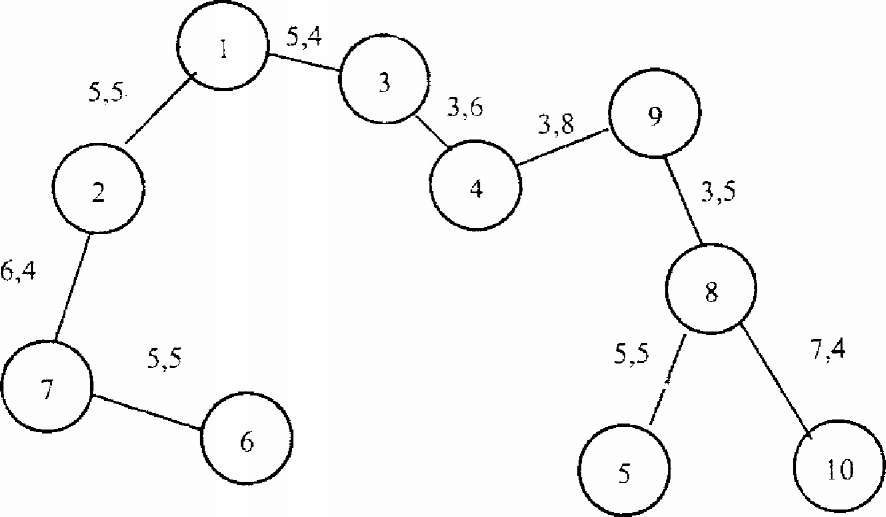
Рисунок Г.1 - Структура НК

ДДодаток Д

ПРИКЛАД ВИКОРИСТАННЯ АЛГОРИТМУ ЛІТТЛА ДЛЯ СИНТЕЗУ ТОПОЛОГІЇ МЕРЕЖІ У ВИГЛЯДІ НАЙКОРОТШОГО ГАМІЛЬТОНОВА

ЦИКЛУ

Визначимо за алгоритмом Літтла найкоротший гамильтонів цикл для

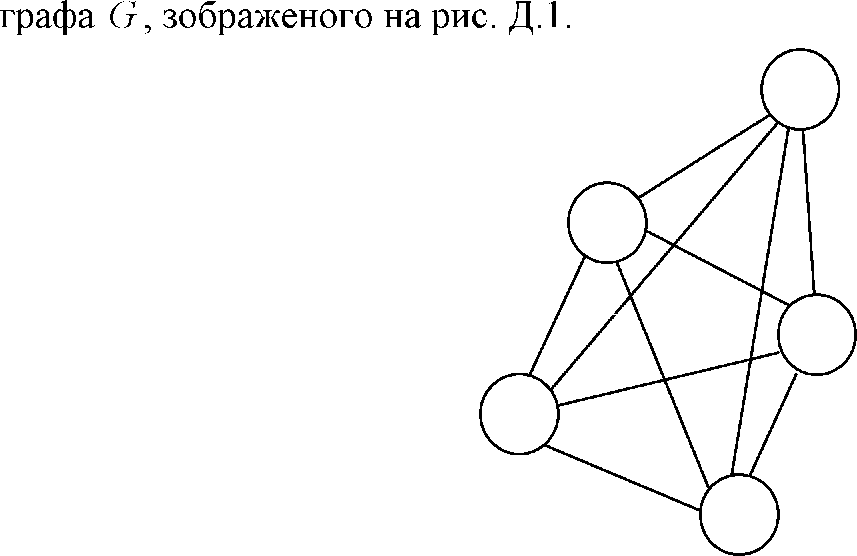
Рисунок Д.1 - Граф G

Матриця відстаней для графа G (рис. Д.1) має вид, показаний на рис. Д.2. Вона є поточною матрицею відстаней для 1 -го кроку алгоритму Літтла L₁ = L:

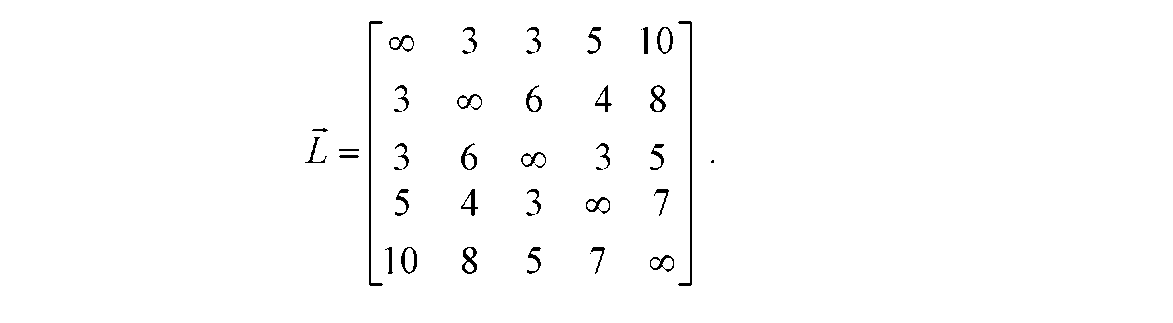
Рисунок Д.2 - Матриця L відстаней графа G

1-й крок. Виконуємо спочатку редукцію рядків поточної матриці Lj відстаней. Для цього в кожнім рядку визначаємо мінімальний елемент і знайдене значення віднімаємо з елементів відповідної рядка. Результати виконання редукції рядків у виді матриці L\ приведені на рис. Д.З, де додатковий вектор - стовпець а містить від'ємники при редукції константи.

Рисунок Д.3 - Скорочена по рядках матриця відстаней на 1 -м кроці алгоритму

Потім виконуємо редукцію стовпців, результати якої у виді матриці L"1 приведені на рис. Д.4, де додатковий вектор - рядок [ містить від'ємники при редукції константи. Значення Y1 елемента, розташованого на перетинанні вектора - стовпця а і вектора - рядка [, дорівнює сумі всіх констант, що віднімаються у₁ = 19. Це значення є нижньою границею L₁(Y) довжин усіх маршрутів на даному кроці: L₁(Y) = ^=19.

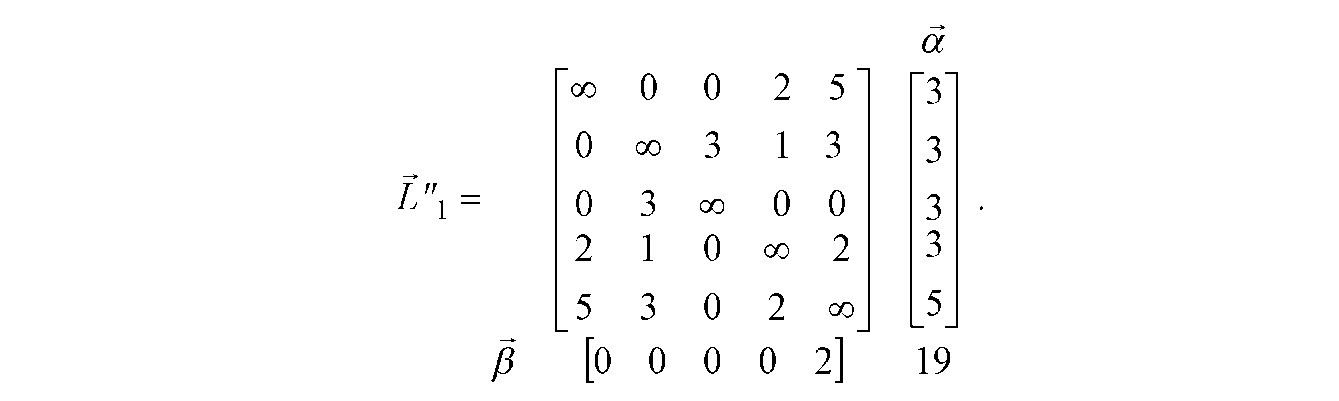
Рисунок Д.4 - Скорочена матриця відстаней на 1-му кроці алгоритму

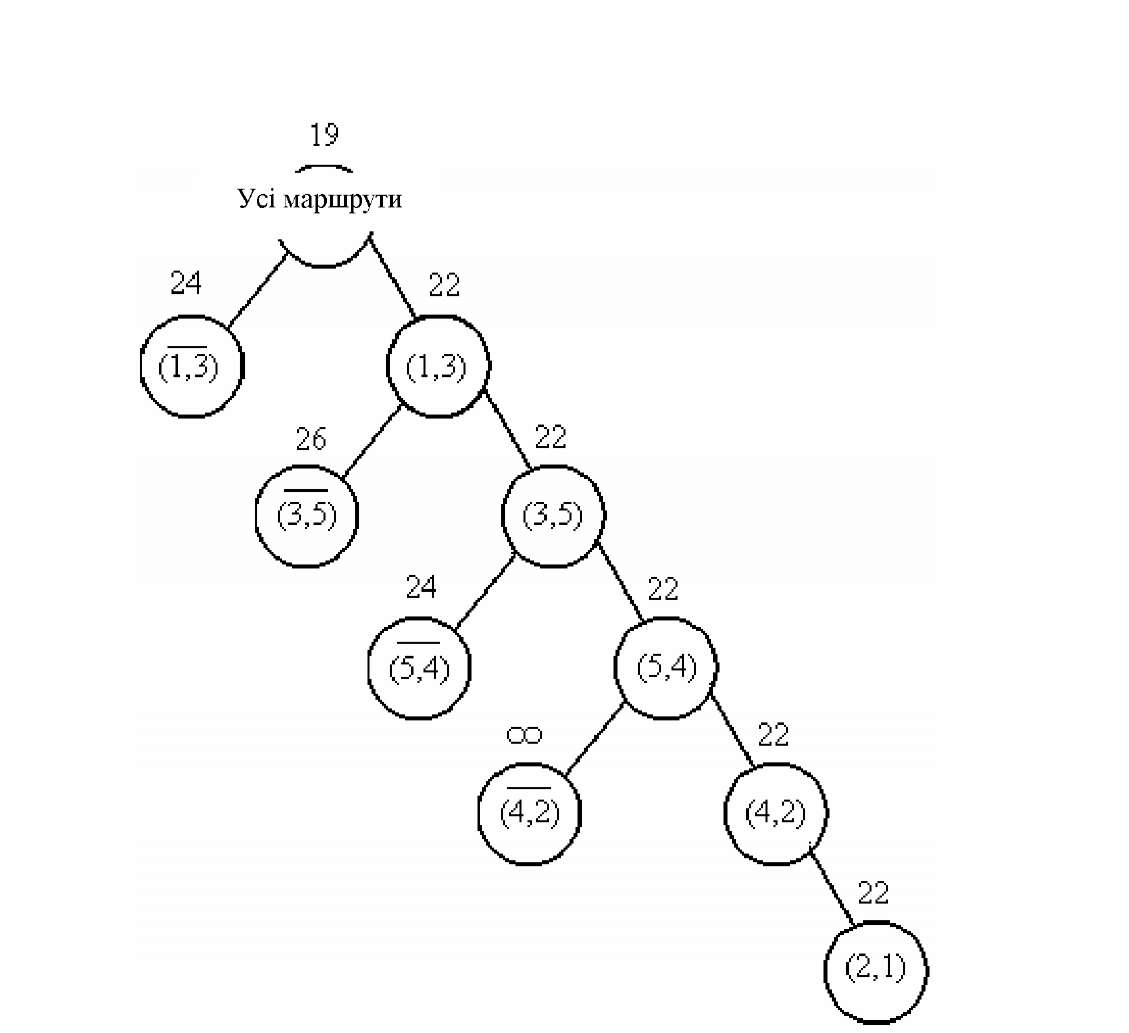
На рис. Д.5 зображений початковий вузол дерева, що відповідає множині всіх маршрутів, і зазначена нижня границя довжин усіх маршрутів.

19

Рисунок Д.5 - Початковий вузол дерева рішень По скороченій матриці L "₁ відстаней далі визначаємо мінімальні

ненульові значення її рядків і стовпців, що записуємо відповідно у виді вектора - стовпця % і вектора - рядка jj. Матриця L "₁ разом з цими векторами показана на рис. Д.6.

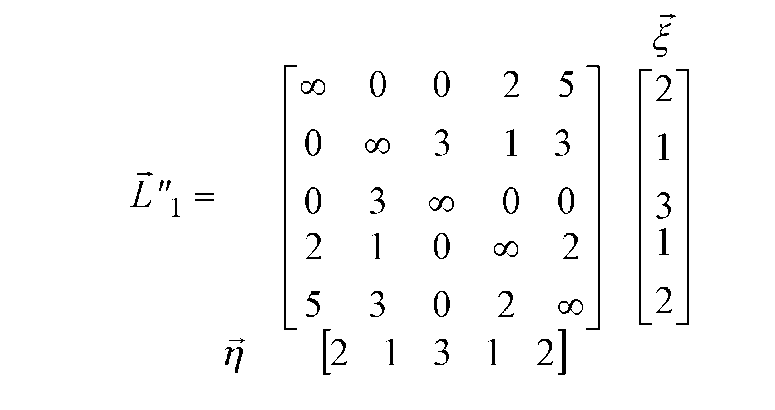
Рисунок Д.6 - Скорочена матриця і значення мінімальних ненульових елементів для 1-го кроку алгоритму

Відповідні елементам векторів % і jj значення вторинних штрафів Sjj для різних ланок чи пар вершин (v_i, v j) з нульовими значеннями відстаней між ними приведені в табл. Д.1.

Таблиця Д.1 - Вторинні штрафи на 1 -м кроці алгоритму

(vi, vj)	£i,j
(vh v2)	3
(vb v3)	5
fe v4)	4
(v3,v5)	5

Як видно з табл. Д.1, максимальне значення s_i j дорівнює 5. Вибираючи ланку (Vi,v₃), можна одержати виграш у відстані, рівний 5, т, е. більший, ніж при виборі будь-якої іншої ланки, за винятком ланки (v₃, v₅). Отже, як базову ланку на 1 -м кроці розгілення вибирається ланка (v₁, v₃), а Y = (1, 3), Y = (1, 3)

Нижньою границею довжин маршрутів з підмножини Y на наступному (2 -м кроці) є величина L₂ (Y) = L₁ (Y) + max є_і j = 24 .

Отже, модифікована матриця L₂ відстаней після викреслювання 1-г

орядка і 3 -го стовпця, а також заміни елемента на перетинанні 3 -й рядка і 1 -го стовпця матриці L\ на да має вигляд, приведений на рис. Д.7.

Рисунок Д.7 - Поточна матриця відстаней для 2-го кроку алгоритму

2-й крок. Виконуємо спочатку редукцію рядків поточної матриці L₂ відстаней. Для цього в кожнім рядку визначаємо мінімальний елемент і знайдене значення віднімаємо з елементів відповідної рядка. Результати виконання редукції рядків у виді матриці L'₂ приведені на рис. Д.8, де додатковий вектор - стовпець а містить від'ємники при редукції константи.

Рисунок Д.8 - Скорочена по рядках матриця відстаней на 2-му кроці алгоритму

Потім виконуємо редукцію стовпців, результати якої у виді матриці L"₂ приведені на рис. Д.9, де додатковий вектор - рядок [ містить від'ємники при редукції константи. Значення у₂ елемента, розташованого на перетинанні

вектора - стовпця а і вектора - рядка [ , дорівнює сумі всіх констант, що віднімаються у2: = 3. Це значення дозволяє визначити нову нижню границю L2(Y) довжин усіх маршрутів на даному кроці: L₂(Y) = L₁(Y) + у₂= 22.

Дерево рішень тепер може бути зображене так, як це показано на рис.

Д.10.

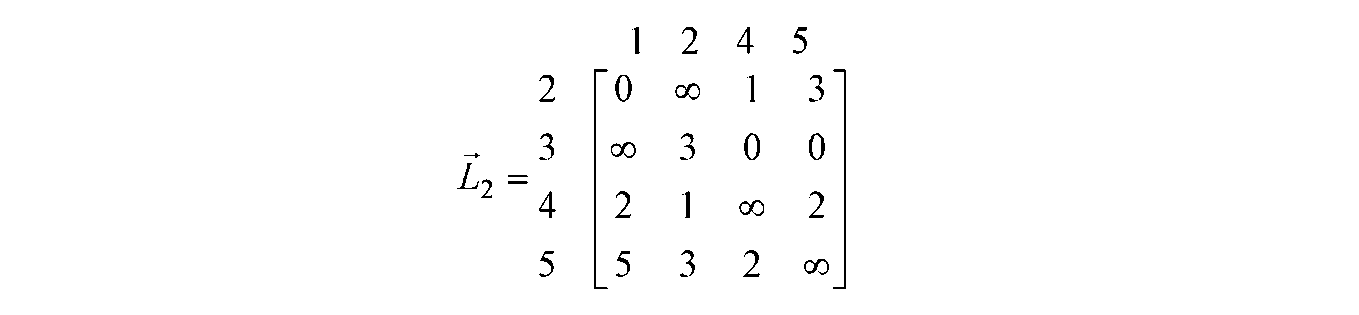
Рисунок Д.11 - Дерево рішень на 2-му кроці алгоритму

Рисунок Д.10 - Скорочена матриця відстаней на 2 -м кроці алгоритму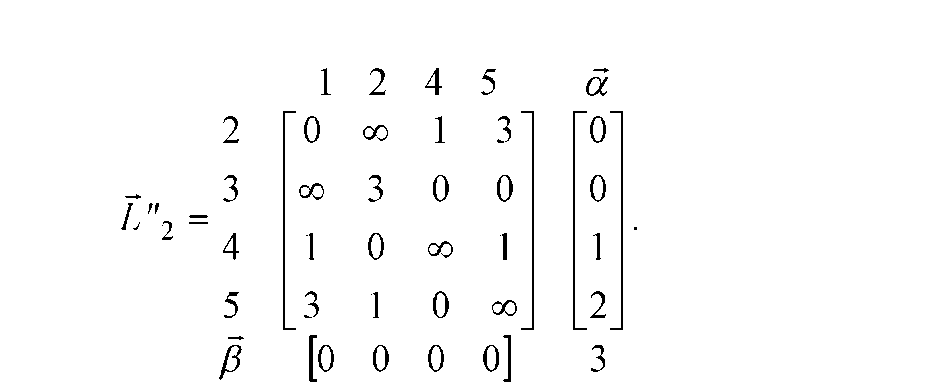

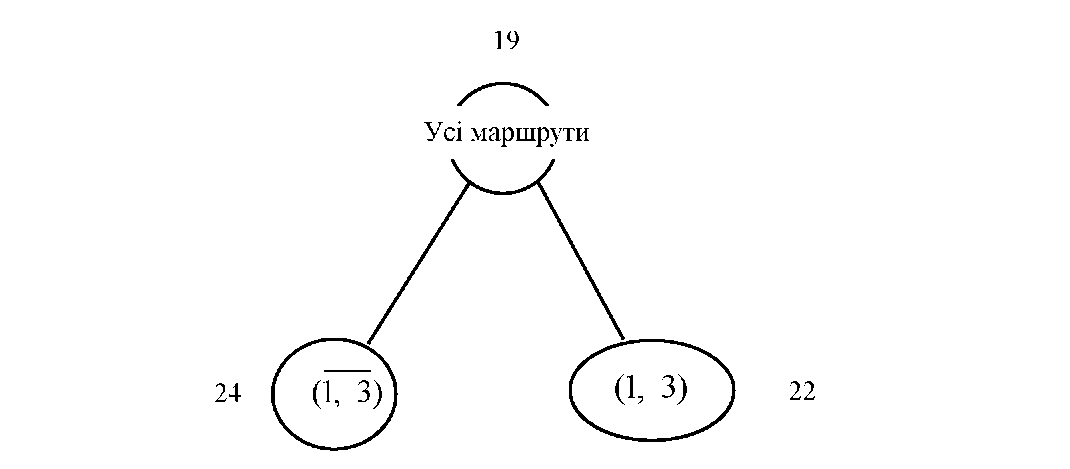
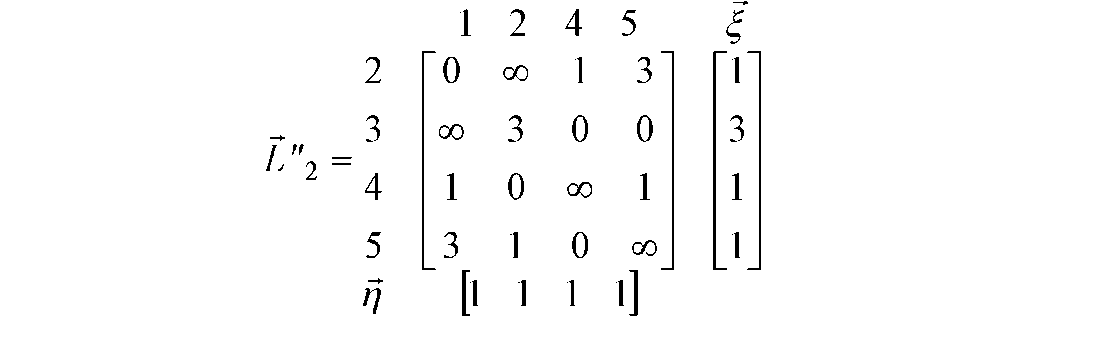
По скороченій матриці L "₂ відстаней далі визначаємо мінімальні ненульові значення її рядків і стовпців, що записуємо відповідно у виді вектора - стовпця ; і вектора - рядка f. Матриця L "₂ разом з цими векторами показана на рис. 1.12.

Рисунок Д.12 - Скорочена матриця і значення мінімальних ненульових елементів для 2-го кроку алгоритму

Відповідні елементам векторів ; і f значення вторинних штрафів j для різних ланок чи пар вершин (v, Vj) з нульовими значеннями відстаней між

ними приведені в табл. Д.2.

Таблиця Д.2 - Вторинні штрафи на 2-му кроці алгоритму (V,, Vj )	є, j
^ v1)	2
V4)	4
V5)	4
(v4,V2)	2
(v5,V4)	2

Як видно з табл. Д.2, максимальне значення s_i j дорівнює 4. Вибираючи ланку (v₃,v₅), можна одержати виграш у відстані, рівний 4, т, е. більший, ніж при виборі будь-якої іншої ланки, за винятком ланки (v₃, v₄). Отже, як базову ланку на 2 -м кроці розгілення вибирається ланка (v₃, v₅), а Y = (3, 4),

Y = (3, 4) Нижньою границею довжин маршрутів з підмножини Y на

наступному (3 -м кроці) є величина L₃(Y) = L₂(Y) + maxs_i j =26.

Модифікована матриця L₃ відстаней після викреслювання 3-го рядка і 5- го стовпця має вигляд, приведений на рис. Д.13.

Рисунок Д.13 - Поточна матриця відстаней для 3-го кроку алгоритму

3-й крок. Виконуємо спочатку редукцію рядків поточної матриці L₃ відстаней. Для цього в кожнім рядку визначаємо мінімальний елемент і знайдене значення віднімаємо з елементів відповідної рядка. Результати виконання редукції рядків у виді матриці L₃ приведені на рис. Д.14, де додатковий вектор - стовпець а містить від'ємники при редукції константи.

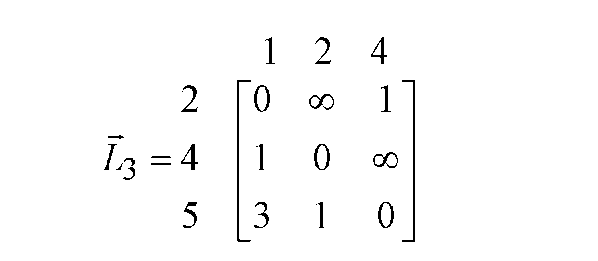
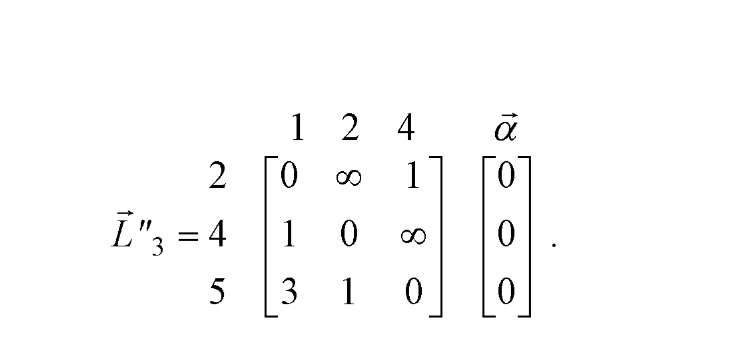
Рисунок Д.14 - Скорочена по рядках матриця відстаней на 3-му кроці

алгоритму

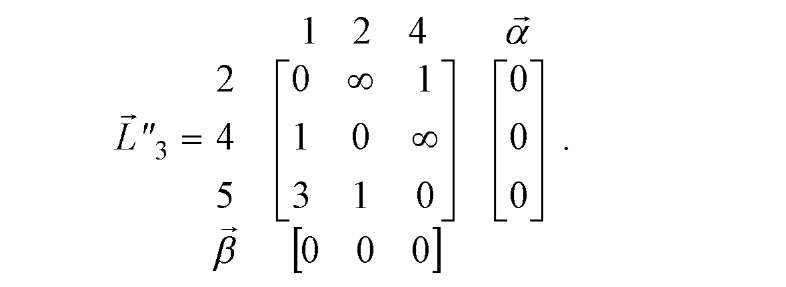
Потім виконуємо редукцію стовпців, результати якої у виді матриці L"₃

приведені на рис. Д.15, де додатковий вектор - рядок [ містить від'ємники при редукції константи. Значення у₃ елемента, розташованого на перетинанні

вектора - стовпця а і вектора - рядка [, дорівнює сумі всіх констант, що віднімаються у₃ =0. Це значення дозволяє визначити нову нижню границю L₃ (Y) довжин усіх маршрутів на даному кроці: L₃ (Y) = L₂ (Y) + у₃ = 22.

Дерево рішень тепер може бути зображене так, як це показано на рис.Д.16.

Рисунок Д.15 - Скорочена матриця відстаней на 3-му кроці алгоритму

Рисунок Д.16 - Дерево рішень на 3-му кроці алгоритму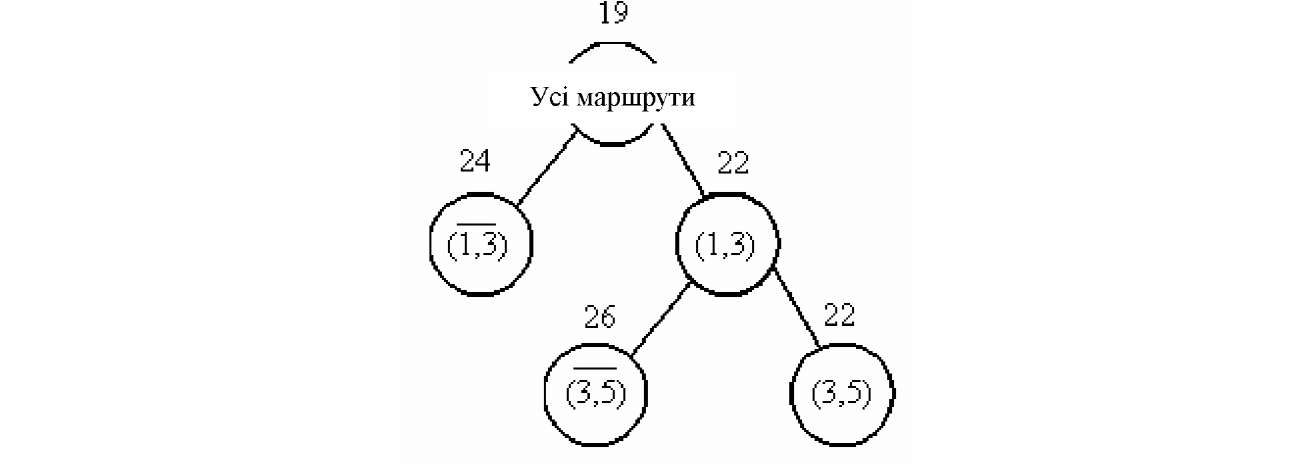

По скороченій матриці L "₃ відстаней далі визначаємо мінімальні ненульові значення її рядків і стовпців, що записуємо відповідно у виді вектора - стовпця % і вектора - рядка rj. Матриця L "3 разом з цими векторами показана на рис. Д.17.

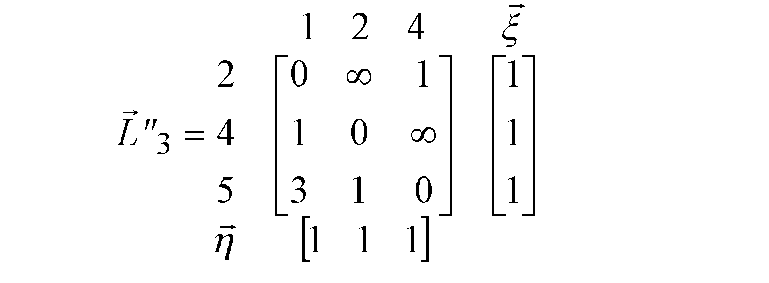
Рисунок Д.17 - Скорочена матриця і значення мінімальних ненульових елементів для 3-го кроку алгоритму

Відповідні елементам векторів % і jj значення вторинних штрафів s_j j для різних ланок чи пар вершин (v_j, Vj) з нульовими значеннями відстаней між ними приведені в табл. Д.3.

Таблиця 1.3 - Вторинні штрафи на 3-му кроці алгоритму (vj, vj)	S, j
(v2, v1)	2
(v4,v2)	2
(v5,v4)	2

Як видно з табл. Д.3, максимальне значення s_j j дорівнює 2 і однаково для всіх ланок. Вибираючи ланку (v₅, v₄), можна одержати виграш у відстані, рівний 2, т, е. Такий же, як і при виборі ланки (v₂, v_:) чи ланки (v₅, v₂). Як базову ланку на 3-му кроці розгілення вибирається ланка (v5, v4), а Y = (5, 4),

Y = (5, 4) Нижньою границею довжин маршрутів з підмножини Y на наступному (4 -м кроці) є величина L₄ (Y) = L₃ (Y) + max s_j j = 24.

Модифікована матриця L₄ відстаней після викреслювання 5-го рядка і 4- го стовпця має вид, приведений на рис. Д.18.

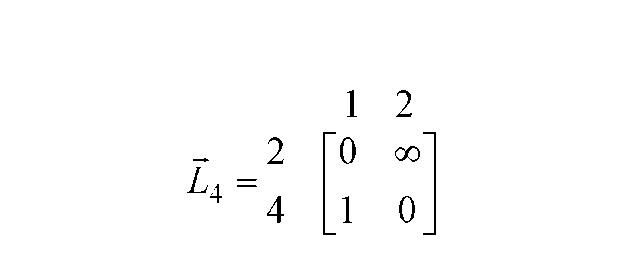
Рисунок Д.18 - Поточна матриця відстаней для 4-го кроку алгоритму

Рисунок Д.20 - Скорочена матриця відстаней на 4-му кроці алгоритму

4-й крок. Виконуємо спочатку редукцію рядків поточної матриці L₄ відстаней. Для цього в кожнім рядку визначаємо мінімальний елемент і знайдене значення віднімаємо з елементів відповідної рядка. Результати виконання редукції рядків у виді матриці L'₄ приведені на рис. Д.19, де додатковий вектор - стовпець а містить від'ємники при редукції константи.

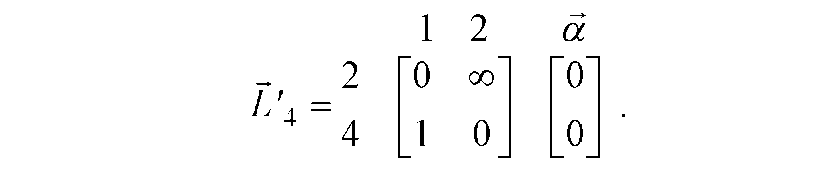
Рисунок Д.19 - Скорочена по рядках матриця відстаней на 4-му кроці

алгоритму

Потім виконуємо редукцію стовпців, результати якої у виді матриці L"₄

приведені на рис. Д.20, де додатковий вектор - рядок Р містить від'ємники при редукції константи. Значення у₄ елемента, розташованого на перетинанні

вектора - стовпця а і вектора - рядка Р, дорівнює сумі всіх констант, що віднімаються у₄ = 0. Це значення дозволяє визначити нову нижню границю L4 (Y) довжин усіх маршрутів на даному кроці: L₄ (Y) = L₃ (Y) + у₄ = 22.

Дерево рішень тепер може бути зображене так, як це показано на рис.

Д.21.

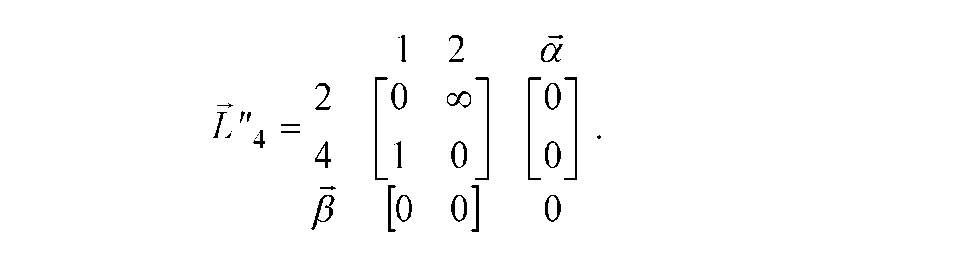
Рисунок Д.21 - Дерево рішень на 4-му кроці алгоритму

По скороченій матриці L "₄ відстаней далі визначаємо мінімальні ненульові значення її рядків і стовпців, що записуємо відповідно у виді вектора - стовпця % і вектора - рядка jj. Матриця L "₄ разом з цими векторами показана на рис. Д.22.

Рисунок Д.22 - Скорочена матриця і значення мінімальних ненульових елементів для 4-го кроку алгоритму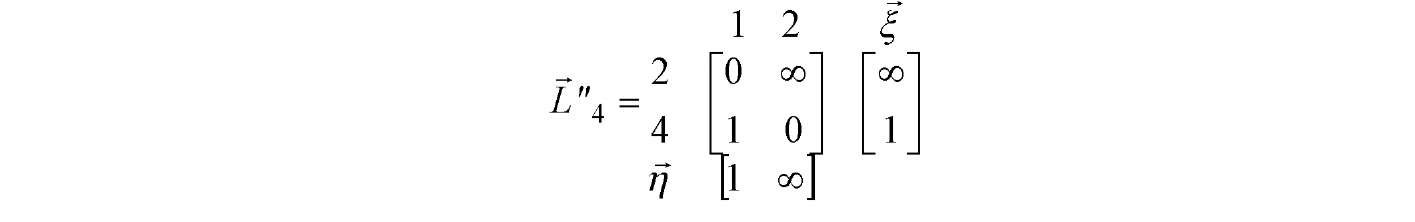

Відповідні елементам векторів % і j значення вторинних штрафів Sj для різних ланок чи пар вершин (v_i , v _j ) з нульовими значеннями відстаней між ними приведені в табл. Д.4.

Таблиця Д.4 - Вторинні штрафи на 4 - м кроці алгоритму (V, Vj)	^ j
(v2, V1)	да
(v4,V2)	да

Як видно з табл. Д.4, максимальне значення s_i j дорівнює да. Вибираючи ланку (v₄, v₂), можна одержати виграш у відстані, рівний да, т, е. більший, ніж при виборі будь-якої іншої ланки, за винятком ланки (v₂, v_:). Як базову ланку на 4-му кроці розгілення вибирається ланка (v₄, v₂), а Y = (4, 2), Y = (4, 2)

Нижньою границею довжин маршрутів з підмножини Y на наступному (5-му кроці) є величина L₅ (Y) = L₄ (Y) + max s_i j = да .

У модифікованій матриці L₅ відстаней після викреслювання 4 -й рядка і 2

-го стовпця залишається один нульовий елемент, що відповідає ланці (v₂, v_:)

(рис. Д.22).

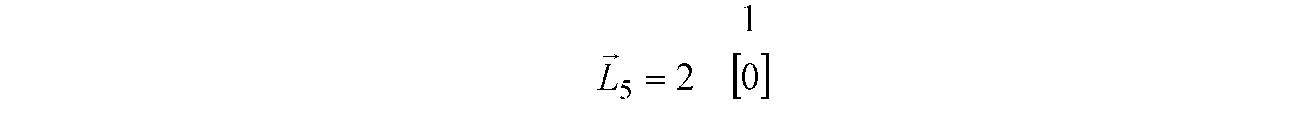
Рисунок Д.22 - Поточна матриця відстаней для 5-го кроку алгоритму

5-й крок. Оскільки в поточній матриці L₅ відстаней мається тільки один нульовий елемент, що відповідає ланці (v₂, v_:), те ця ланка є останнім в обумовленому маршруті довжиною L₅(Y) = L₄(Y )=24.

Дерево рішень тепер може бути зображене так, як це показано на рис.

Д.24.

Побудований повний маршрут є оптимальним, якщо його довжина не перевершує довжини будь-якого маршруту, що відповідає іншим ланкам дерева, що і має місце в даному прикладі. Він складається з наступних ланок чи пар вершин m_opt = {(v_b v₃), (v₃, v₅), (v₅, v₄), (v₄, v₂), (v₂, v_:)} і має сумарну довжину

L(m₀p_t) =22. Цей оптимальний маршрут є мінімальним гамильтоновим циклом,

що зображений на рис. Д. 25.

Рисунок Д.25 - Мінімальний гамильтонів цикл графа G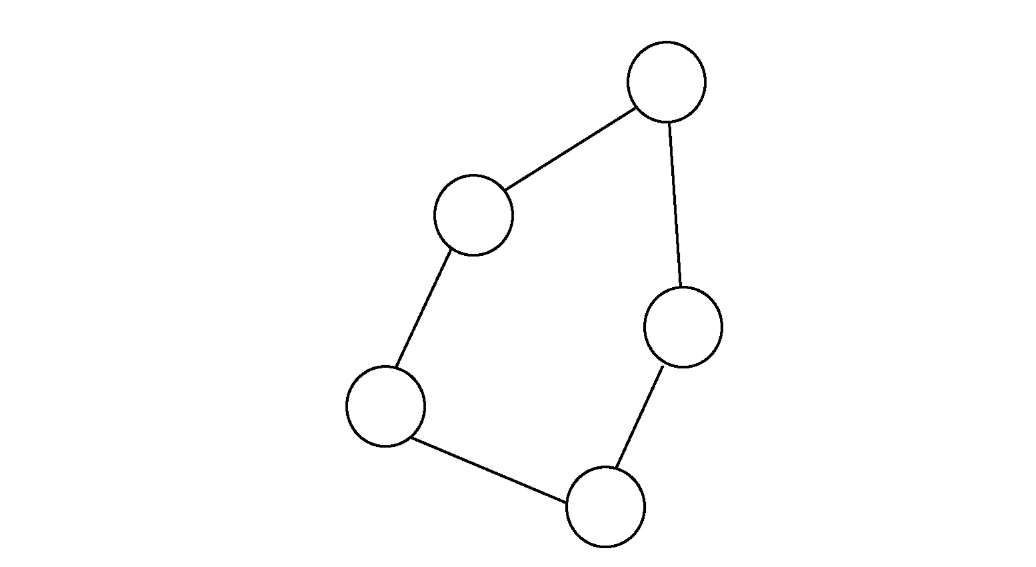

Додаток Е

ПРИКЛАД ВИКОРИСТАННЯ МЕТОДУ ПОБУДОВИ ДЕРЕВА ДЛЯ ВИЗНАЧЕННЯ МНОЖИНИ ШЛЯХІВ

V (u₁ A u2 A u₆ A u₄) V (u₁ A u₂ A u₆ A u₃).

Для графа (рис. Е.1) побудуємо дерево шляхів з вершини 1. Дана вершина є коренем дерева і розміщається на нульовому ярусі. Значення рангу шляху тут R = 0. На першому ярусі (R =1) розміщаються вершини 2, 4, 5, що мають безпосередній зв'язок з вершиною 1. Далі на другому ярусі від вершини 2 розміщаються вершини, що зв'язані з вершиною 2, а саме 3 і 5. Вершина 1 виключається з розгляду, оскільки шлях у вершину 2 пройшов через вершину 1. Від вершини 4 на другому ярусі записуються вершини 3 і 5, від вершини 5 — вершини 4 і 3. Аналогічно записуються вершини на інших ярусах дерева.

Рисунок Е.1 - Граф мережі Введемо позначення для ребер (дуг) змішаного графа мережі (рис. E.1):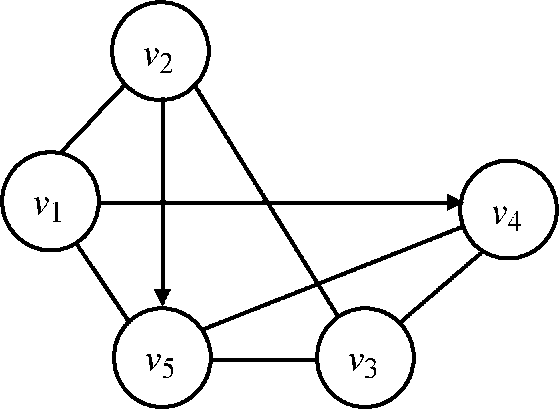

^u1 = ^(v1, ^v2 ⁾ ' ^u2 = ^(v2' ^v3⁾. ^u3 = ^(v3> ^v4 ⁾ ' ^u4 = ^(v4' ^v5⁾. ^u5 = ^(v1> ^v5⁾. ^u6 = ^(v3> ^v5⁾. ^u7 = ^(v2' ^v5 ⁾ ' ^u8 = ^(v1> ^v4⁾ .

Побудоване дерево для вершини-джерела 1 представлене на рис. Е.2. З цього дерева можна одержати множину шляхів з фіксованої вершини в будь-яку вершину графа послідовним переглядом ярусів дерева. Цю множину шляхів можна записати як диз'юнкцію кон'юнкцій символів ребер (дуг), що утворять кожний із шляхів розглянутої множини.

Наприклад, для пари вершин v₁, v₄ множина шляхів записується у вигляді

M_{1 4} = u₈ V (u₅ A u₄) V (u₁ A u2 A u₃) V (u₁ A u₇ A u₄) V (u₅ A u₆ A u₃) V

R = 0 R = 1 R = 2 R = 3 R = 4

Рисунок Е.2 - Дерево шляхів з вершини-джерела 1.

Додаток Є

ПРИКЛАДИ АНАЛІЗУ СТРУКТУРНОЇ НАДІЙНОСТІ МЕРЕЖІ

Визначимо надійність зв'язку к_г (M₁₃) між пунктами (вузлами) V₁ і V₃ мережі, граф якої зображений на рис. Є.1, використовуючи позначення к_гa, к_гь , к_гс, к_гd для коефіцієнтів готовності його ребер a, b, с, d, відповідно.

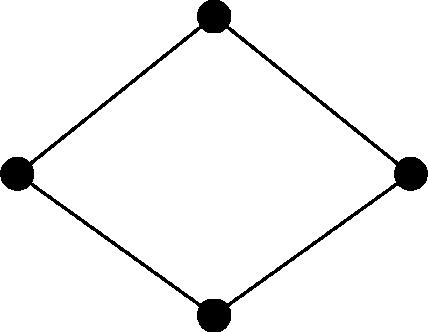
Рисунок Є.1 - Граф мережі з паралельними шляхами

В даному випадку множини паралельних шляхів, кожний з яких є послідовним з' єднанням його ребер:

При наявності перемички між шляхами - ребра e з коефіцієцієнтом готовності к_г буде мати місце містковий граф мережі (рис. Є.2, а), для якого

використовуємо метод послідовного розкладання топології мережі.

Відповідно до цього метода у випадку місткового графа мережі (рис. Є.2, а) при e =1 одержимо топологію, показану на рис. Є.2, б, а при e =0 - на рис. Є.2, в

.

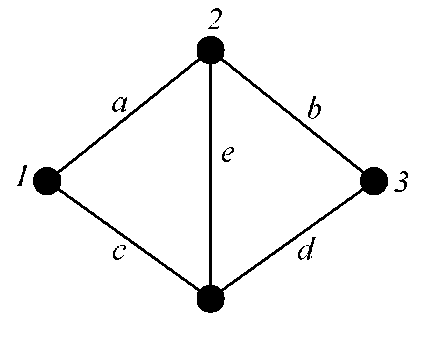
4

a) ^б)

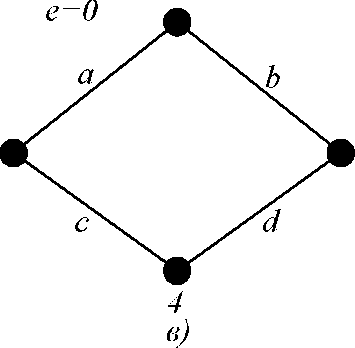
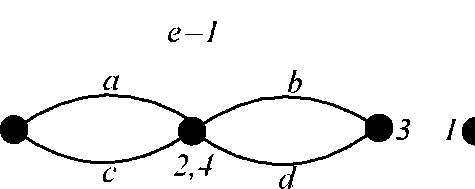
Рисунок Є. 2 - Перетворення місткового графа мережі

Для цих топологій ймовірність збереження зв'язності визначається за звичайними формулах додавання й множення ймовірностей (коефіцієнтів готовності):

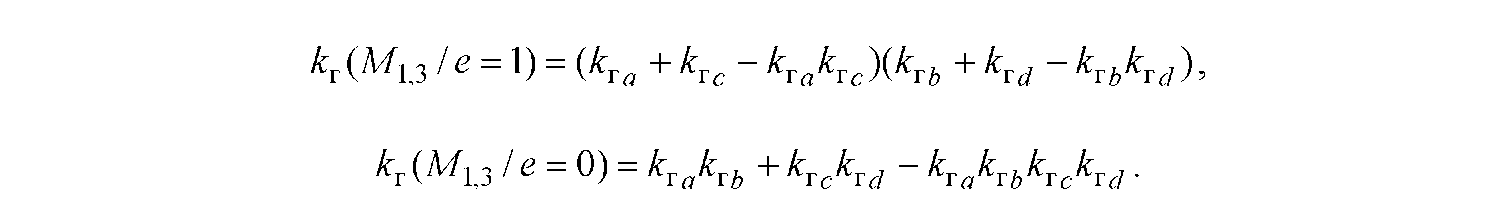
Результуюча надійність зв'язку (3.7) між пунктами v₁ та v₃:

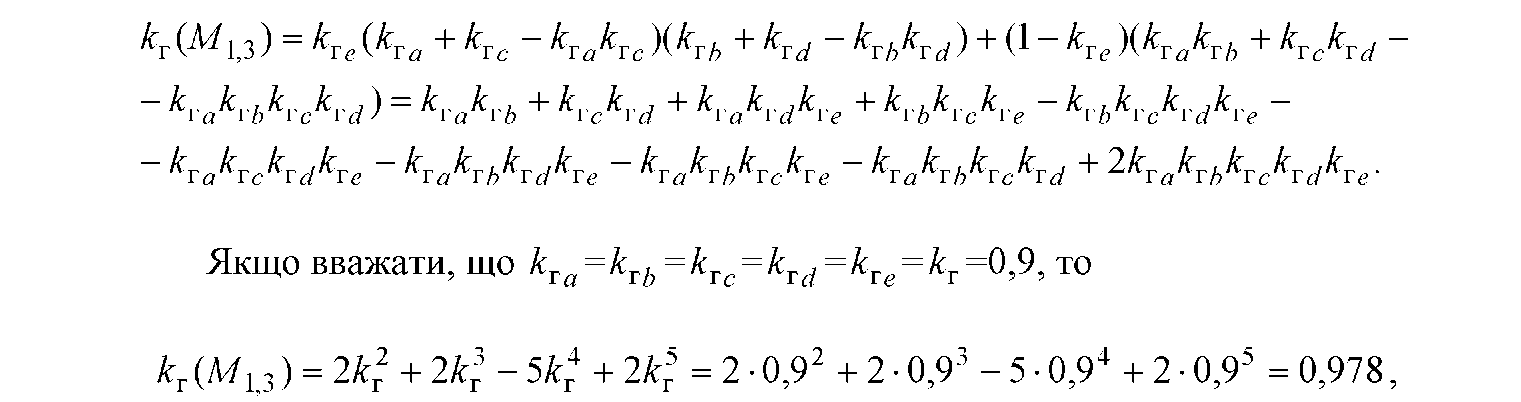
тобто надійність зв'язку при наявності перемички між шляхами вище, ніж при паралельних шляхах

.Додаток Ж

ПРИКЛАД ВИКОРИСТАННЯ АЛГОРИТМУ ДЕЙКСТРИ ДЛЯ ВИЗНАЧЕННЯ ОПТИМАЛЬНИХ ПО ДОВЖИНІ МАРШРУТІВ ВІД ЦЕНТРАЛЬНОГО

ВУЗЛА ДО ІНШИХ

Знайдемо з використанням алгоритму Дейкстри найкоротші шляхи від вершини - джерела v₀ до інших вершин орграфа мережі на рис. Ж. 1.

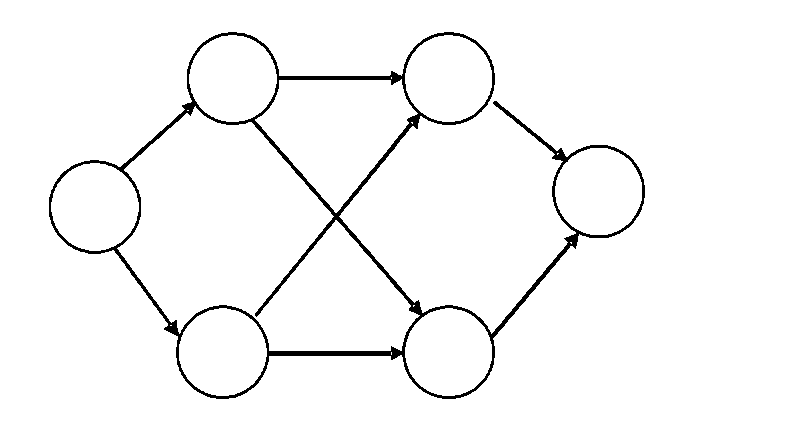
Рисунок Ж. 1 - Зважений орграф мережі

Розв'язання. Застосуємо алгоритм Дейкстри: Крок 1. w₀ = 0, wj = да для всіх j ф 0.

Крок 2. n = 0. Крок 3.

Крок 4. «Позначаємо» вершину vj та дугу (v0, vj). Крок 5. n = 1.

Крок 6. Визначаємо, що не всі вершини «позначені». Крок 3.

Крок 4. «Позначаємо» вершину V3 та дугу (vj,V3). Крок 5. n = 3.

Крок 6. Визначаємо, що не всі вершини «позначені»

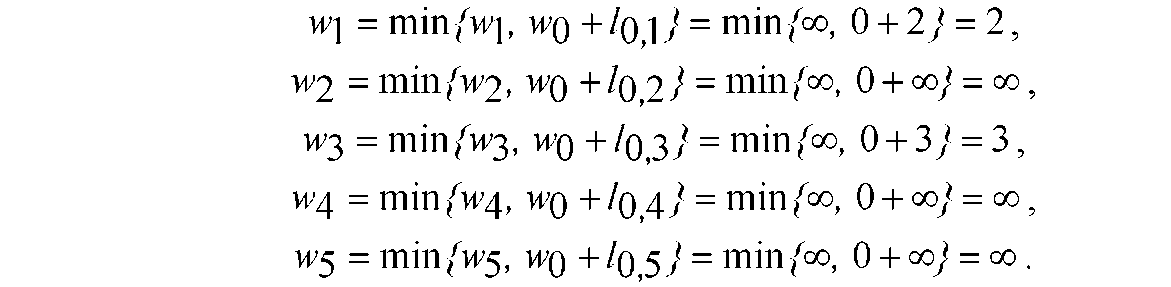
.Крок 3.

Крок 4. «Позначаємо» вершину v4 та дугу (vj, v4). Крок 5. n = 4.

Крок 6. Визначаємо, що не всі вершини «позначені». Крок 3.

Крок 4. «Позначаємо» вершину v₂ та дугу (v₁, v₂ ) . Крок 5. n = 2 .

Крок 6. Визначаємо, що не всі вершини «позначені». Крок 3.

W5 = min {W5, w2 +l2,5} = min {11, 7 +1} = 8 Крок 4. «Позначаємо» вершину v₂ та дугу (v₂ , v₅ ) . Крок 5. n = 5.

Крок 6. Визначаємо, що всі вершини «позначені».

«Позначені» вершини й дуги утворять орієнтоване дерево найкоротших шляхів, яке наведене на рис. Ж.2.

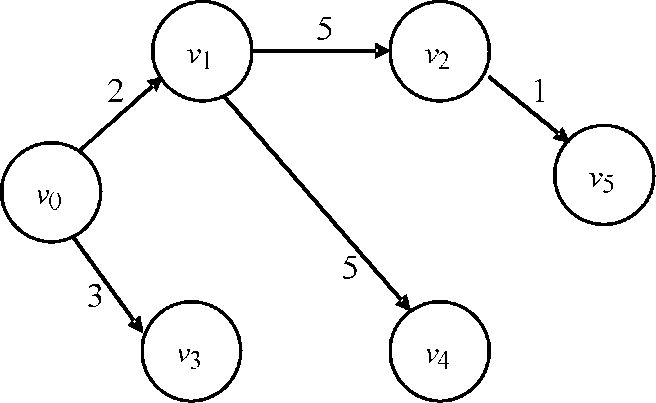
Рисунок Ж.2 - Дерево найкоротших шляхів від вершини - джерела v0 до інших

Крок 3.

вершин вихідного графа мережі

Додаток З

ПРИКЛАДИ ПОСТАНОВКИ ТА РОЗВ'ЯЗАННЯ ЗАДАЧ ВИБОРУ ПРОПУСКНИХ СПРОМОЖНОСТЕЙ (ВПС) КАНАЛІВ ЗОНОВИХ МЕРЕЖ

ЗВ'ЯЗКУ З КОМУТАЦІЄЮ ПАКЕТІВ

З.1 Постановка задач ВПС

Нехай повнозв'язний граф мережі з комутацією пакетів має вигляд, показаний на рис. З. 1.

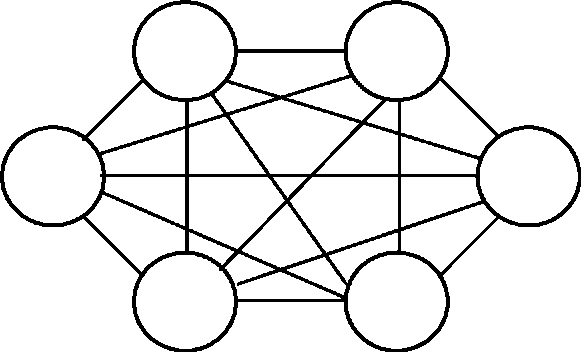
Рисунок З.1 - Повнозв'язний граф мережі з комутацією пакетів Задаємося вектором інтенсивностей зовнішніх потоків

матрицею відстаней між вузлами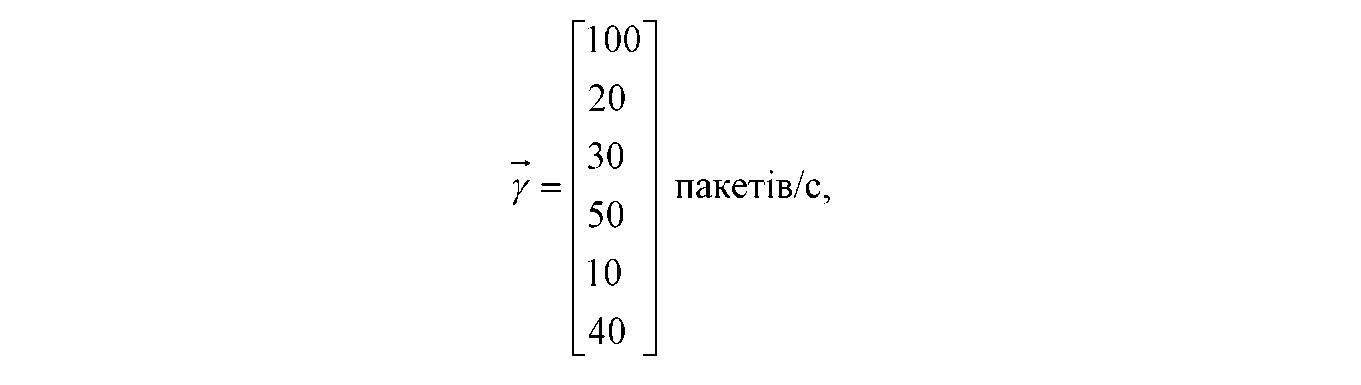

та середньою довжиною пакетів n =100 октетів.

В результаті використання метода М-структур можна отримати комірчасту топологію мережі, яка при з'єднаннях «точка - багатоточка» показана на рис. З.1, а дерево найкоротших шляхів від центрального вузла до інших вузлів мережі за алгоритом Дейкстри - на рис. 3.2.

Рисунок 3.1 - Комірчаста топологію мережі при з'єднаннях «точка -

багатоточка»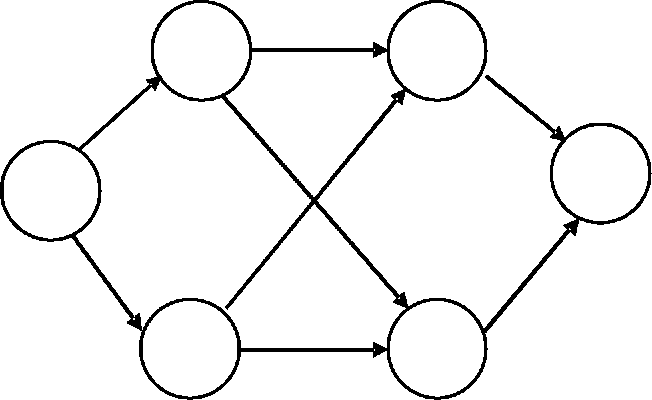

Рисунок 3.2 - Дерево найкоротших шляхів від центрального вузла до інших

вузлів мережі за алгоритом Дейкстри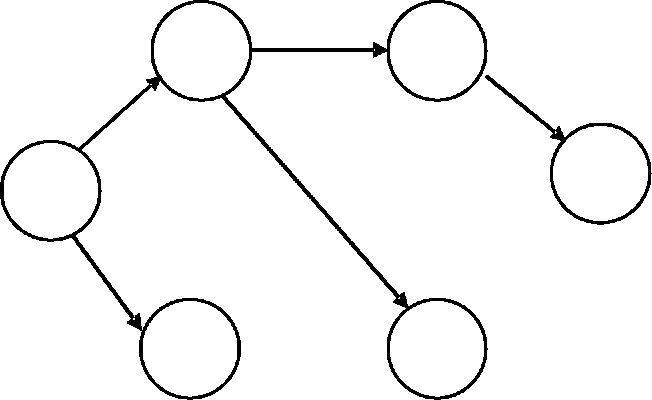

Розрахуємо характеристики інформаційного тяжіння між центральним та іншими вузлами.

Визначаємо коефіцієнти інформаційного тяжіння за навантаженням відповідно (3.11):

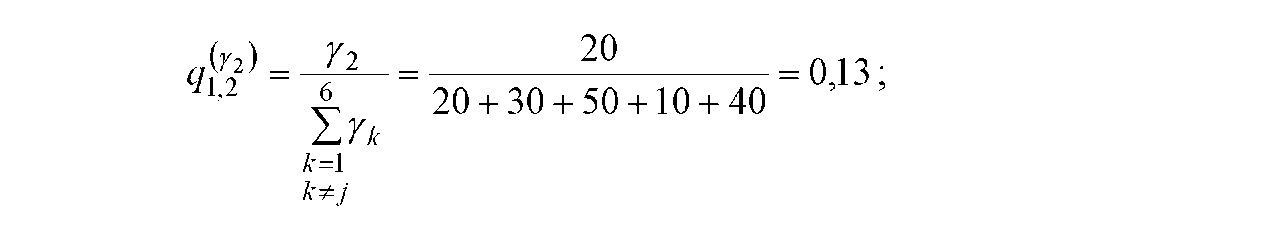
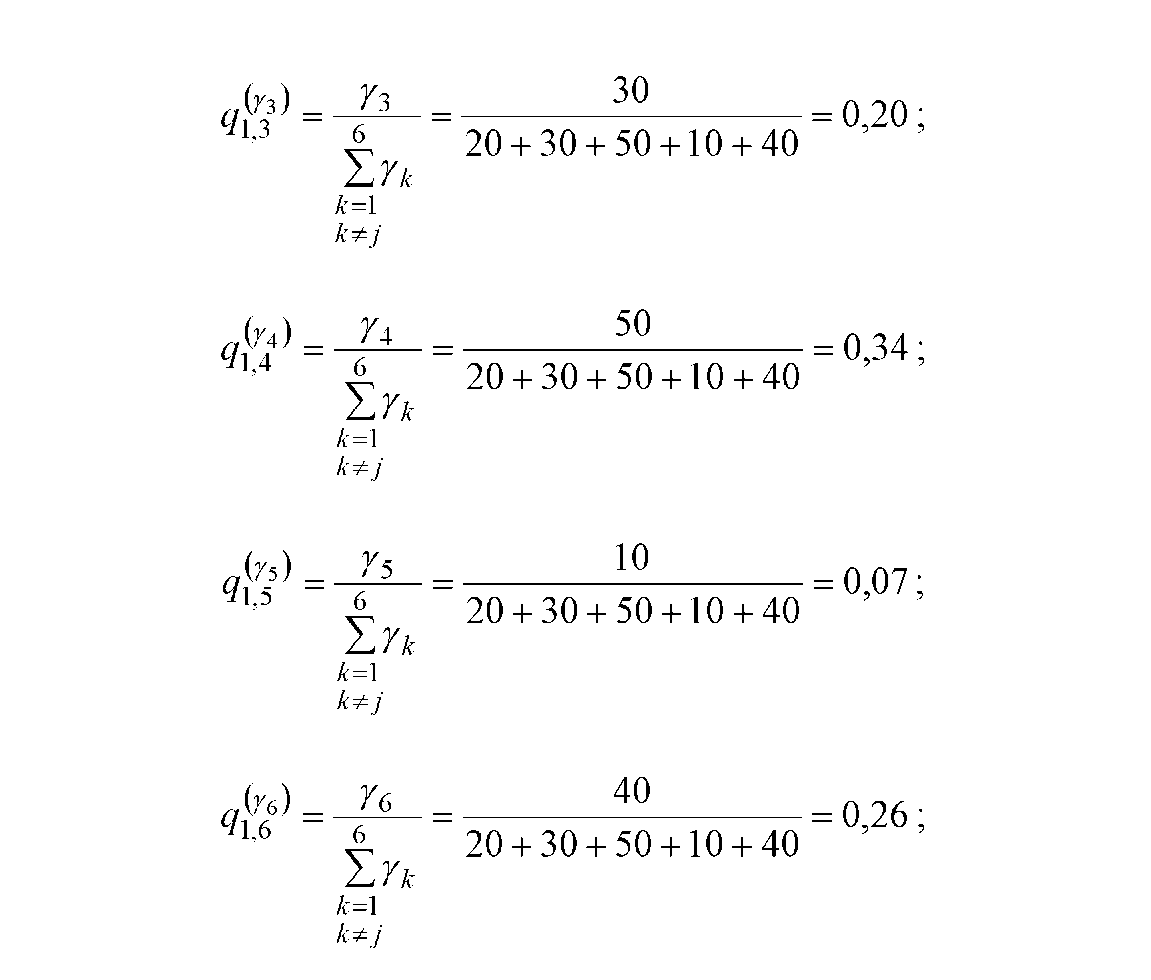
коефіцієнти інформаційного тяжіння за відстанню відповідно (3.12) при параметрі її впливу a =1:

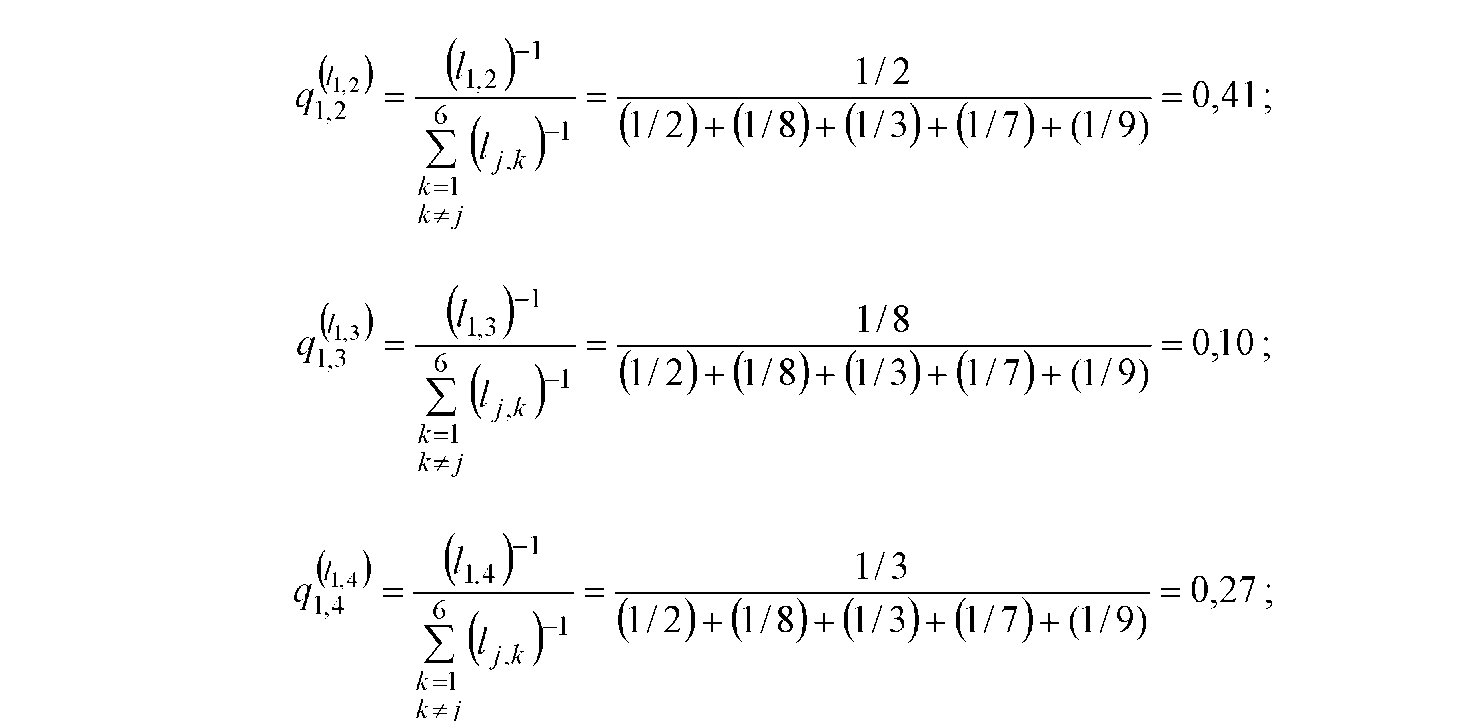
результуючі коефіцієнти інформаційного тяжіння відповідно (3.10):

к Ф j

Інтенсивністі зовнішніх (міжвузлових) потоків відповідно (3.9):

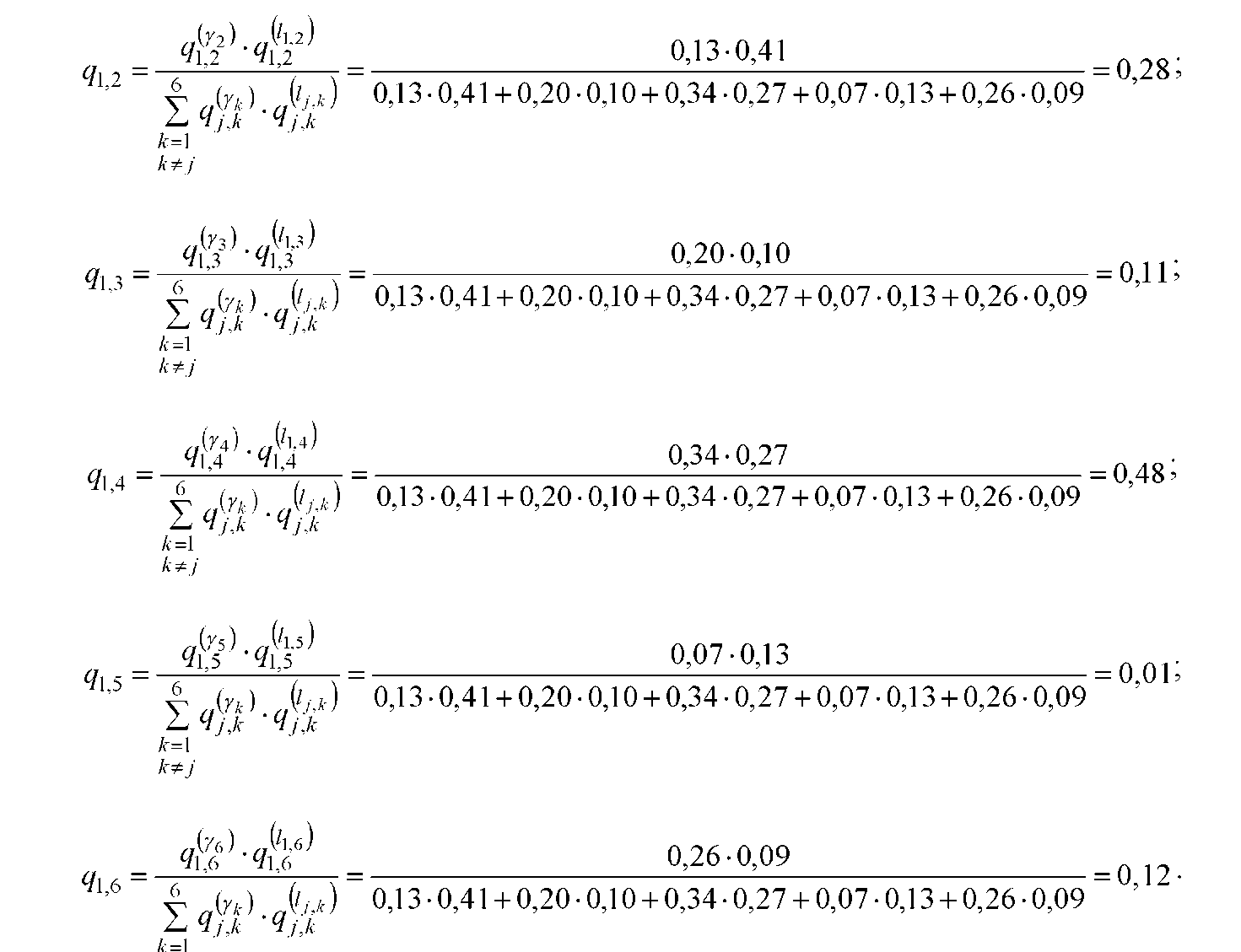
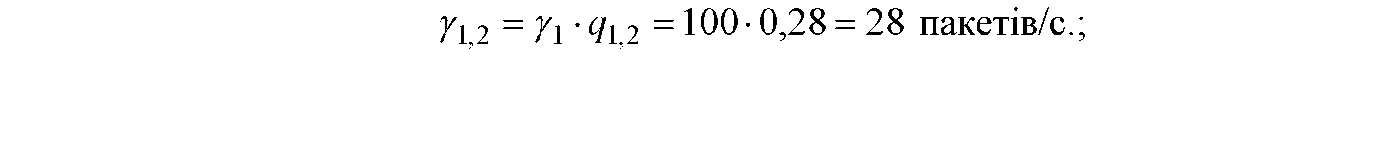
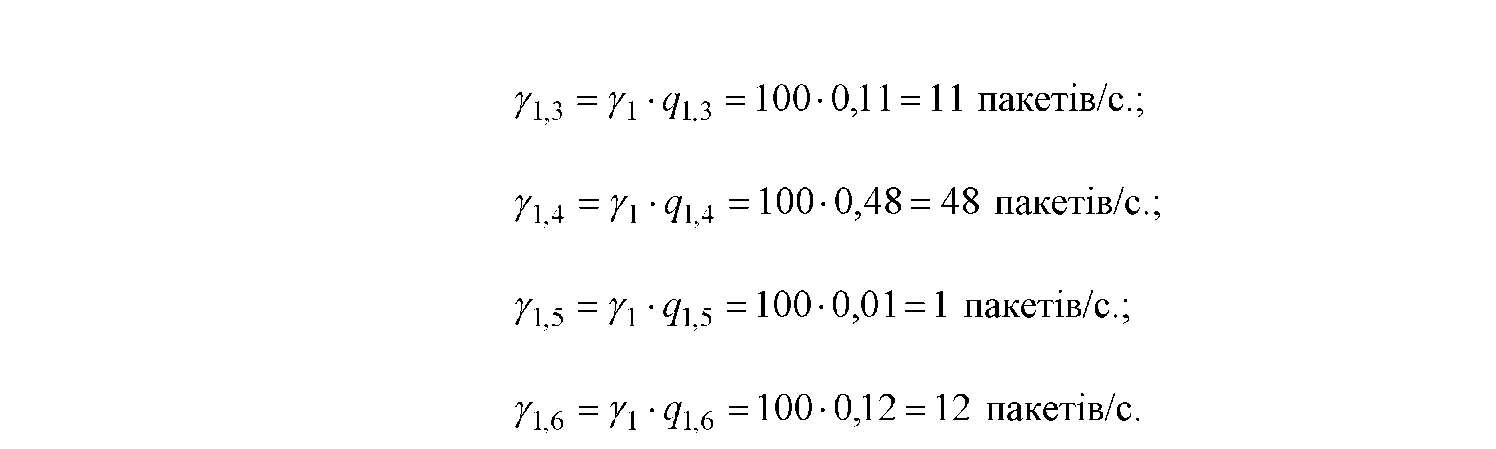
При цьому сумарна інтенсивність зовнішніх потоків пакетів від центрального до інших вузлів буде у =100 пакетів/с.

Використовуючи характеристики інформаційного тяжіння між центральним та іншими вузлами мережі, для дерева шляхів (рис. З. 2) одержимо наступні значення інтенсивностей внутрішніх потоків, що відповідають каналам:

Інтенсивність загального внутрішнього потоку пакетів в мережі при односпрямованому трафіку від центрального вузла до інших буде

3.2 Приклад розв'язання в системі математичного програмування Mathcad задачі ВПС за критерієм мінімуму середньої затримки пакетів при обмеженні на сумарну пропускну спроможність C <2048 кбіт/с

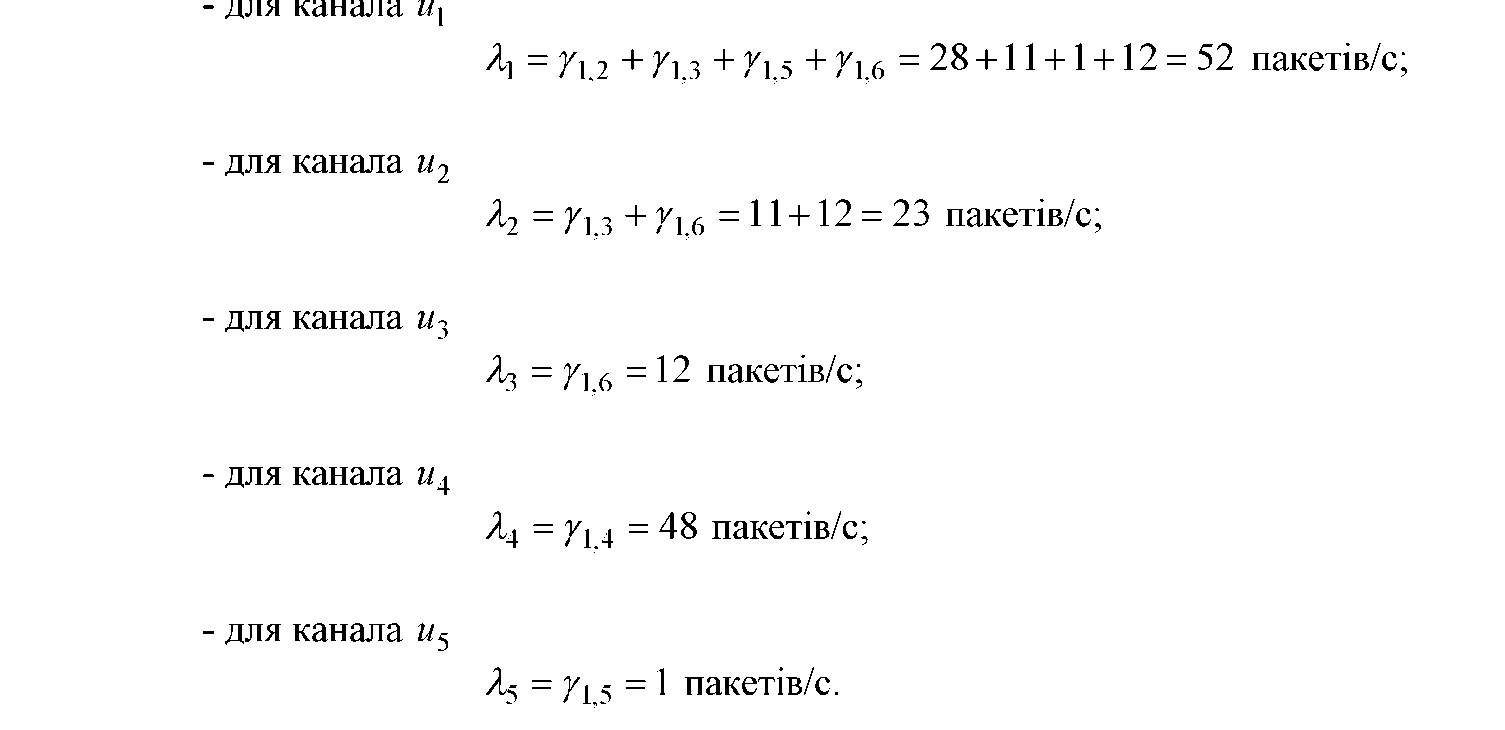
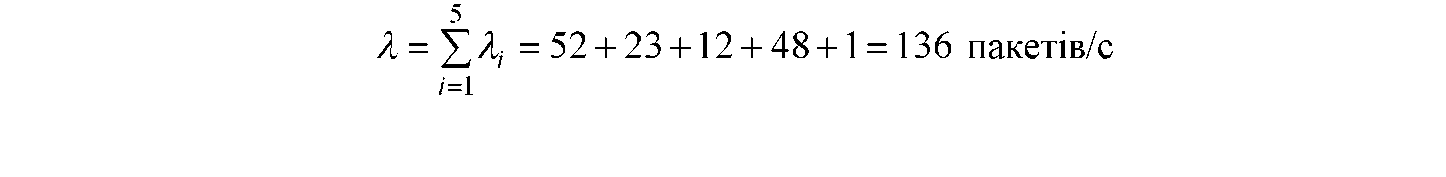
3.3 Приклад розв'язання в системі математичного програмування Mathcad задачі ВПС за критерієм мінімуму сумарної пропускної спроможності при обмеженні на середню затримку пакетів T < 3 мс

Навчальне видання

МЕТОДИЧНІ ВКАЗІВКИ ДО КУРСОВОГО ПРОЕКТУВАННЯ З ДИСЦИПЛІНИ "ТЕЛЕКОМУНІКАЦІЙНІ ТА ІНФОРМАЦІЙНІ МЕРЕЖІ"

для студентів усіх форм навчання напряму 6.050903 "Телекомунікації"

Упорядники: БІДНИЙ Юрій Михайлович

БУХАНЬКО Олександр Миколайович

Відповідальний випусковий В.М. Безрук Редактор

Комп'ютерна верстка

План 2011 поз. Формат 60Х84 1/16 Спосіб друку - ризографія

Підп. до друку Облік. вид. арк. Тираж 100 примір.

Умов. друк. арк.

Замов. № Ціна договірна