
6.1.3.Формула Симпсона
Применяя интерполяционную формулу Лагранжа при n = 2, получим значения коэффициентов:
![]()
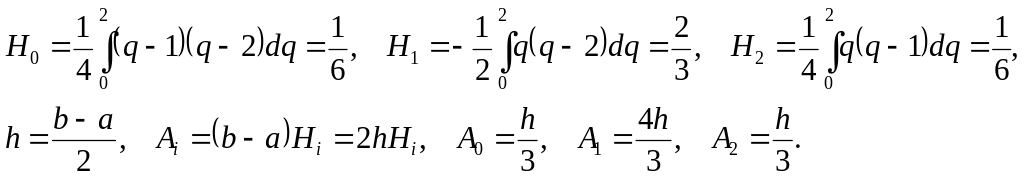 .
.
![]() (6.15)
(6.15)
Геометрический смысл формулы Симпсона (6.15) заключается в том, что кривая y = y(x) заменяется частью параболы, проходящей через три точки (x0, y0), (x1, y1) и (x2, y2).
Формула Симпсона точна не только для полинома второй степени, но и для полинома третьей степени в силу симметрии, показанной на рис. 6.4б.
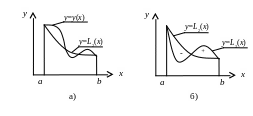
Рис.6.4
Остаточный член формулы (6.15) имеет порядок O(h5).
Общая формула Симпсона строится для четного n = 2m; при этом формула (6.15) применяется для каждого из отрезков [x0, x2], [x2, x4], …, [xn–2, xn]:
![]() .
(6.16)
.
(6.16)
Поменять местами второе и третье; h/3 вынести за знак суммы
Остаточный член общей формулы Симпсона (6.16) имеет порядок O(h4).
Пример 6.2. Вычислить по формуле Симпсона (6.16) интеграл
,
используя разбиение отрезка на n = 10 частей.
Решение. Проведем вычисления в программе Excel. В столбце A и B запишем значения индекса i и переменной x. В ячейку B2 вводим формулу =sin(B2)/B2 и маркером заполнения копируем в ячейки B3:B12. В ячейках D2:D12 вводим коэффициенты при yi общей формулы Симпсона (6.16). В ячейку D13 вводим формулу =СУММПРОИЗВ(C2:C12;D2:D12)*0,1/3. Результаты вычислений приведены в таблице 6.2.
Табл. 6.2
|
A |
B |
C |
D |
1 |
i |
xi |
yi |
Коэффициенты |
2 |
0 |
1 |
1 |
1 |
3 |
1 |
1,1 |
0,909091 |
4 |
4 |
2 |
1,2 |
0,833333 |
2 |
5 |
3 |
1,3 |
0,769231 |
4 |
6 |
4 |
1,4 |
0,714286 |
2 |
7 |
5 |
1,5 |
0,666667 |
4 |
8 |
6 |
1,6 |
0,625 |
2 |
9 |
7 |
1,7 |
0,588235 |
4 |
10 |
8 |
1,8 |
0,555556 |
2 |
11 |
9 |
1,9 |
0,526316 |
4 |
12 |
10 |
2 |
0,5 |
1 |
13 |
|
Интеграл= |
|
0,693150231 |
Найдем относительную погрешность
![]()
Как видим, формула Симпсона дает более высокую точность по сравнению с методом трапеций.
Создадим в файле программы Excel для решения примера 6.2 макрос — функцию для вычисления интеграла по формуле Симпсона (6.16).
С помощью меню «Сервис — Макроc — Редактор Visual Basic» откроем окно редактора, выполним команду «Insert — Module» и введем программы
Function f(x): f = 1 / x: End Function
Function Int_Simpson(a, b, n)
s = 0: h = (b - a) / n: h2 = h * 2: x = a
For i = 0 To n - 2 Step 2
s = s + f(x) + 4 * f(x + h) + f(x + h2): x = x + h2
Next i
Int_Simpson = h * s / 3: End Function
Теперь, если в ячейку D14 введем формулу =Int_Simpson(1;2;10), получим приближенное значение 0,693150231.
