6. Система координат графика и её положение на канве

Пусть координаты некоторой точки в системе координат графика (x,y), а в системе канвы (в пикселях) – (X, Y).

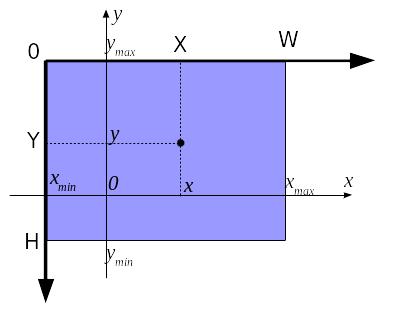
Так как оси системы графика параллельны соответствующим осям системы координат канвы, X в пикселях будет зависеть только от x, а Y – только от y.

Рассмотрим преобразование абсцисс:

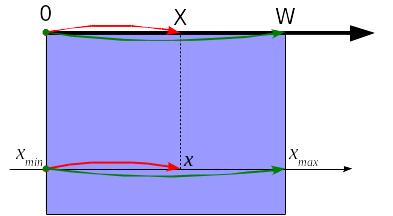
7. Оси абсцисс графика (0x) и канвы (0x)

Рассмотрим отрезки, имеющие в системе графика координаты [x_min, x] и [x_min, x_max]. Очевидно, что в системе канвы они должны выглядеть как [0, X] и [0, W], т.е. можно записать:

откуда можно выразить X через x:

или наоборот, x через X:

Аналогично, для ординат можем записать:

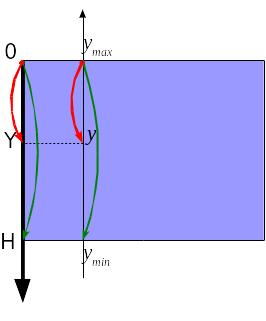
8. Оси ординат графика и канвы

откуда получаем:

и

Рассмотрев вместо [0, Y] и [y_max, y] отрезки [Y, H] и [y, y_min], получим и . Как можно убедиться, эти формулы эквивалентны приведенным выше.

Пример 5. Рисование по пикселям.

float X, Y; //координаты точек изображаемой функции

int PX, PY; //координаты соответствующих им пикселей

float Xmax, Xmin, Ymax, Ymin; //координаты максимальных и //минимальных значений X и Y для данного отрезка функции,

//необходимые для масштабирования графика и его равномерного

//расположения на экране

for(PX = 0; PX <= Image1->Width; PX++)

{

X = Xmin + PX*(Xmax - Xmin) / Image1->Width;

Y = F(X); //F(X) – функция, график которой мы хотим //построить

PY = Image1->Height - (Y - Ymin)*Image1->Height / (Ymax - Ymin);

//Будем рисовать красным цветом:

Image1->Canvas->Pixels[PX][PY] = clRed;

}

Здесь Image1Height и Image1Width - высота и ширина экрана (в пикселях).

Пример 13.6. Рисование функции y = cos(x) на отрезке x[0, 2].

Для данной функции X изменяется на отрезке от 0 до 2, Y – от -1 до 1, поэтому Ymin = -1, Ymax = 1.

Создаем форму и помещаем на нее компонент Image и кнопку с надписью y = cos(x).

Обработчик события OnDblClick (двойной щелчок левой кнопкой мыши) будет иметь вид:

#define PI 3.14159 //или const float Pi = 3.14159;

float X, Y, Xmax=2*Pi, Xmin=0, Ymax=1,Ymin=-1;

int PX, PY;

for(PX=0; PX<=Image1->Width; PX++)

{

X = Xmin + PX*(Xmax-Xmin) / Image1->Width;

Y = cos(X);

PY = Image1->Height - (Y-Ymin)* Image1->Height / (Ymax-Ymin);

Image1->Canvas->Pixels[PX][PY] = 0x00080808;

}

Если нужен непрерывный рисунок, используют свойство Pen – перо, которое в свою очередь, тоже имеет ряд свойств: Color –цвет, Width – ширина линии в пикселях (по умолчанию – 1), Style – вид линии.

Свойство канвы PenPos определяет текущую позицию пера. Перемещение пера без прорисовки линии осуществляется методом канвы MoveTo(X, Y). Метод LineTo(X, Y) рисует линию от текущего положения пера к точке с координатами (X, Y).

Пример 13.7. Рисование графика из примера 13.6 с помощью пера. Для использования константы M_PI следует подключить заголовочный файл math.h.

float X, Y, Xmax=2*M_PI, Xmin=0, Ymax=1, Ymin=-1;

int PX, PY;

PX = 0;

X = Xmin + PX*(Xmax-Xmin) / Image1->Width;

Y = Cos(X);

PY = (Ymax - Y)* Image1->Height / (Ymax-Ymin);

Image1->Canvas->MoveTo(PX, PY);

for(PX=1; PX<=Image1->Width; PX++)

{

X = Xmin+PX*(Xmax-Xmin) / Image1->Width;

Y = Cos(X);

PY = (Ymax - Y)* Image1->Height / (Ymax-Ymin);

Image1->Canvas->LineTo(PX, PY);

}

С помощью пера можно рисовать не только линии, но и фигуры, как показано в табл.1.

Таблица 1

Методы объекта Canvas

Arc		Дуга
Chord		Дуга + хорда
Ellipse		Эллипс или окружность
Pie		Сектор
Polygon		Замкнутый полигон
Polyline		Разомкнутый полигон
Rectangle		Прямоугольник или квадрат
RoundRect		Прямоугольник или квадрат со скругленными углами

Пример 8. Изобразить бирюзовый эллипс, ограниченный желтым контуром

void __fastcall TForm1::FormPaint(TObject *Sender)

{

Canvas->Pen->Color=clYellow; //цвет контура

Canvas->Brush->Color=clAqua; //цвет заливки

Canvas->Ellipse(15, 15, 60, 60); //эллипс

}

Пример 9. Изобразить и

Polygon Polyline

void __fastcall TForm1::FormPaint(TObject *Sender)

{

TPoint points[5]; //задаем массив точек многоугольника

points[0]=Point(30, 150);

points[1]=Point(40, 130);

points[2]=Point(50, 140);

points[3]=Point(60, 130);

points[4]=Point(70, 150);

PaintBox1->Canvas->Polygon(points, 4);

PaintBox1->Canvas->TextOut(30, 170, "Polygon");

points[0].x+=100;

points[1].x+=100;

points[2].x+=100;

points[3].x+=100;

points[4].x+=100;

PaintBox1->Canvas->Polyline(points, 4);

PaintBox1->Canvas->TextOut(130, 170, "Polyline");

}

или

void __fastcall TForm1::FormPaint(TObject *Sender)

{

TPoint points[3] = {Point(10,10), Point(10,100), Point(100,10)};

Canvas->Polyline(points, 2);

}

В данных примерах мы рисуем на канве формы и на на канве компонента TPaintBox с вкладки System, но не на более удобном TImage. Так сделано потому, что компонент TImage имеет собственный механизм прорисовки, и его изменение снова вызывает перерисовку. Помещение подобных действий в обработчик события OnPaint формы (перерисовки окна) может привести к некорректной отрисовке некоторых дочерних элементов формы.