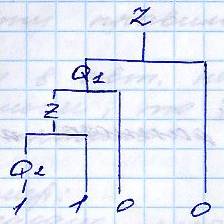
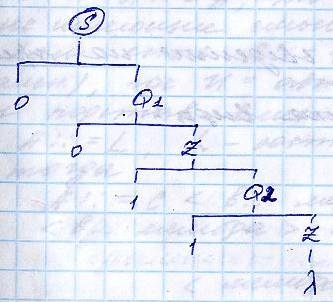
Правостороняя, левосторонняя и т.Д.
Разбираем цепочки из пары един. символов
α = 00110011110000.
Представление разбора в данном виде есть не что иное как синтаксическое дерево.
|
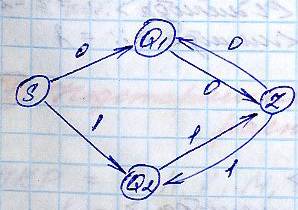
Q1::= 0 | Z 0 Q2 ::= 1 | Z 1 Z ::=Q1 0 | Q2 1 → получили грамматику
|
Грамматика порождает язык, автомат разбирает язык.
Грамматика, у которой правила представлены в виде Q::=T или Q::=UT носит название автоматной грамматики (в данном случае левосторонняя)
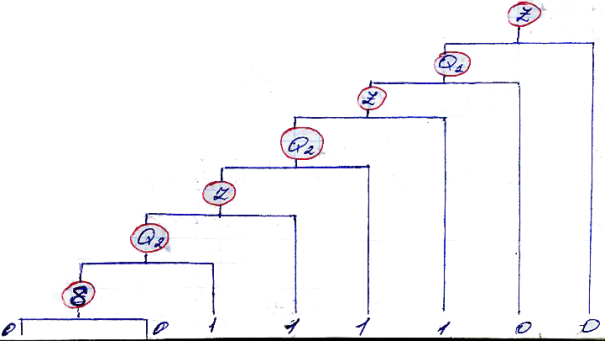
Z → Q21 → Z11 → Q1 011 → 0011
Правосторонняя автоматная гр-ка имеет правила вывода U::=TQ. Она обычно используется для автомат. описания к грамматике. Переход заключается в следующем:
1) Словарем термин. слов грамматики сделать все входные символы автомата. 2) Мн-во состояний автомата сделать словарем нетермин. символов При этом начальным символом грамматики считается начальное состояние автомата. 3) Если в автомате имеется переход из состояния А в состояние В по условию Т, то вводится правило А ::=TB. Если в автомате некоторое состояние Z является конечным, для этого состояния надо завести правило Z::=λ
|
S::=0 Q1 | 1 Q2 Q1 ::= 0 Z Q2 :: = 1 Z Z::= 0 Q1 | 1 Q2 | λ
|
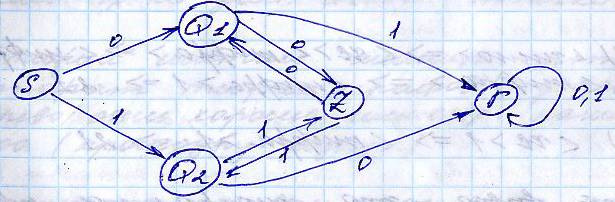
Переход от грамматики к автомату
Дана некоторая ( например левосторонняя) автоматная грамматика A [Z]
1) Чтоб построить эквивал. конеч. автомат, необх. завести начальное сосотояние S. 2) если в гр-ке есть правила вида Qn::=Tn, n=1,2,3...,то в данном случае надо построить следующее
3)
Если в автомате есть правила вида U
::= TQ
то необходимо построить
п
ри
построении каждое правило отождествляется
с состоянием данного автомата.
Правосторонние грамматики тоже довольно легко свести к автомату.
НКА и ДКА должны обрабатывать один и тот же входной язык.
НКА → {KVMSZ} ДКА → { K’V’M’S’Z’ }
Алгоритм преобразования
1) Ввести в ДКА столько состояний, сколько подмножеств можно построить из состояний НКА.
2) Всем состояниям ДКА присвоить имя по правилу (см. ниже)
3) Ввести начальное состояние ДКА
4) Ввести мн-во заключительных состояний ДКА
5) Построить все частичные ф-ции переходов в ДКА (по правилу)
правило
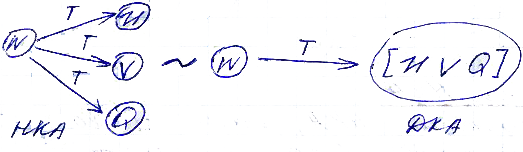
Имя [U V Q] эквивалентно всему левому подмножеству.
В ДКА вводится столько состояний, сколько существует подмножеств состояний в НКА и каждому состоянию в ДКА присваивается имя в [] и в [] записываются все имена из НКА.
В НКА S = {S1,S2,S3} в ДКА [S1 S2 S3]
V – входной алфавит НКА V=V’
В экв. ДКА состояние, в имени которого встречается хотя бы одно Zi,тоже надо обозначить как заключительное состояние.
Регулярное выражение – это ǿ, λ, S1, S2....
Если е – рег.врж. тогда (е) и {e} тоже регуляр. врж-я
Если е1 и е2 – рег. врж-я, то е1е2 и е1/е2 тоже являются регулярными выражениями.
Значение Р.В. - | е |
Если | ǿ |, то | ǿ | = ǿ, |λ| = λ, |S| = S
Если |e1/e2|, то |e1/e2| = |e1| U |e2|, |e1e2| = |e1||e2| - конкатенация
|{е}| = | e | *
A*={λ}UA1UA2
В модифицированной нотации Бэкуса-Наура правая часть правил представляет собой регулярное врж-е. Исключение – отсутствие в грамматиках вывода ǿ и λ.
Система переходов – специфическая диаграмма состояний, строящаяся на основе регулярных выражений. Имеет всегда одно начальное и одно конечное состояние. Она допускает все цепочки, описываемые регулярным выражением. В общем виде
Существуют базовые конструкции сис-мы переходов
Р.В. |
Система переходов |
ǿ |
|
λ |
|
Si |
|
e1/e2 |
|
e1e2 |
|
{e} |
|
Регулярное врж. можно представить в виде композиции элементарных регулярных врж-й => систему переходов можно построить как систему регулярных конструкций.