1)ДКА – это пятерка вида (К V M S Z), где

К – алфавит состояний распознавателя

V – входной алфавит

M – функция перехода M=K x V →K

S – начальное состояние S Є K

Z – множество заключительных состояний

Принцип работы распознавателя:

На его вход поступает буква за буквой цепочка символов и в соответствии с тем, этот ли класс цепочек надо распознать, формируется выход распознавателя. Входная цепочка символов – некоторая последовательность букв входного алфавита. Например, А = {a,b,c}= aabca,  - пустая цеп.

Автомат начинает работу с состояния S. Если работа автомата заканчивается в одном из состояний Z, то цепочка считается распознанной. Если в каком-либо другом состоянии – нераспознанной. Автомат можно представить в виде графа, где вершины – состояния, а дуги взвешены символами входного алфавита. Либо можно задать таблицей, где по горизонтали – символы вход. алф., а по вертикали – симв. алфавита ДКА. На пересечении их – возможный переход в данное состояние по данному условию.

K = M (K,V) – функция перехода

2) Синтез автомата – построение его описания в виде таблицы переходов. Как правило в нач. синтеза задается некот. алгоритм функц-я устройства.

3) Рассмотрим метод ролей на примере задачи построения конечного автомата для распознавания веществ. чисел в языке Basic. Для начала выпишем несколько типовых способов записи веществ. чисел в Basic. Например:

12Е+08, 12Е08, 12Е-08, 12, .12, 12.5

Разобьем литеры на классы {Ц , знак, Е, . }, где

Ц = {1,2,3….9}, знак = {+,-}, Е=Е, . = .

Выпишем след. числа

1123 4 5 6 733 4 6 6 - № роли

12.5Е+5 .12Е12 12.Е

Теперь распишем все роли:

1 – цифра, стоящая до десятич. точки, 2 - десятичная необязательная точка, 3 - цифра, стоящая после десятич. точки, 4 – символ порядка, 5 – знак порядка,

6 – цифра порядка, 7 – обязательная десятичная точка

После того как над посл-ю сформир. роли всех символов, каждая роль отождествляется с состоянием конечного автомата и строится таблица переходов. (F-ошибка)

	Ц	Е	.	знак	y/n
S	1	F	7	F	n
1	1	4	2	F	y
2	3	4	F	F	y
3	3	4	F	F	y
4	6	F	F	5	n
5	6	F	F	F	n
6	6	F	F	F	y
7	3	F	F	F	n

4) Минимизация автоматов

С уть её заключается в том, что бы постролить такой автомат, который имел бы тmin количество состояний. Используя понятие эквивалентности. На множестве состояний нужно построить классы эквивалентностей. Пример: Пусть задан следующий конечный распознаватель.

Минимизация автомата начинается с удаления всех недостижимых состояний (вершин). Недостижимое – это такое состояние, в которое нельзя попасть из начального состояния S (в нашем примере B3, B4, Z). Удаляем эти состояния вместе со связями (дугами) Выполним эти действия.

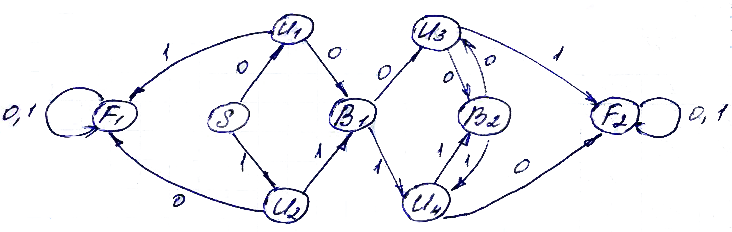
Эквивалентные состояния. Рассмотрим ниже понятие эквивалентности. Состояние является в полном смысле математическим понятием отношения эквивалентности на множестве состояний. Два состояния А и В являются эквивалентными , если для них выполняются:

- Условие подобия. Очевидно, что А и В, если они эквивалентны, должны быть либо допускающие, либо отвергающие.

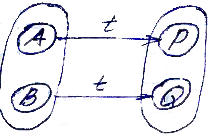- Условие преемственности. Любая цепочка Т из входного алфавита переводит эту пару так же в другую пару состояний, которые эквивалентны.

P = M(A, t) Q = M(B, t) P~Q

Тривиальный алгоритм поиска эквивалентных состояний основан на методе таблиц эквивалентности.

Метод эквивалентных таблиц основан на пр-ке функций переходов – на исследовании формулы M(A, t) ~ M(B, t). Выбирается пара, для неё строиться пустая таблица эквивалентности. На каждый входной символ заполняется новая пара состояний. Если во вновь полученных парах присутствует пара, в которой условие подобия не совпадает => исходная пара не эквивалентна. Если во вновь полученной паре подобие соблюдается, но условие соблюдается преемственности неявно, то эта пара записывается в 1й столбец таблицы и выч. для неё произв. след. обр.

Так выделяется множество эквивалентных состояний. Трудоёмкость метода < n^2., т.к. при исследовании пар эквивалентности состояний сразу выясняются эквивалентные множества других пар.

Проделав эту процедуру на нашем примере:

=> Эквивалентные состояния: (U1, U3) (U2, U4) (B1, B2) (F1, F2)

Полное выявление всех состояний нужно каждому эквивалентному подмножеству состояний дать некоторое имя.

(U1, U3) -> U1

(U2, U4) -> U2

(B1, B2) -> B

(F1, F2) -> F

В таблице переходов имя каждого эквивалентного состояния заменяется на имя подмножества

И щем одинаковые строки и вычёркиваем их. Получим новую таблицу:

В соответствии с новой таблицей переходов нужно нарисовать автомат:

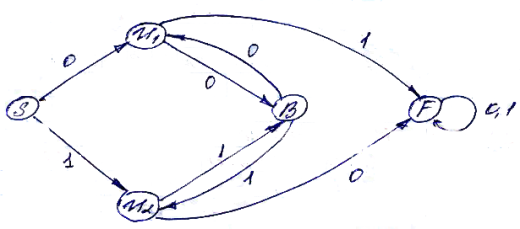
Минимизация автомата выполнена в 2 приёма:

1. Удаление недостижимых состояний

2. Поиск эквивалентных состояний.

Минимизация методом разбиения на блоки

Суть разберём на нашем примере (вопрос №9).

1. Все исходные состояния разбиваются на 2 блока по эквивалентности: допускающие и не допускающие.

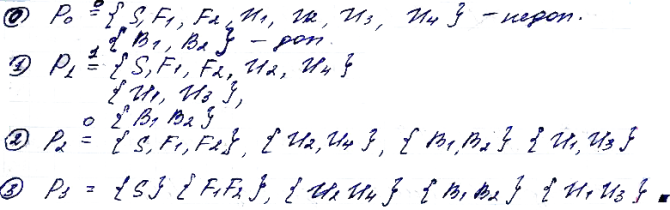
На последних шагах разбивают состояния на блоки по преемственности: если преемник находиться в том же блоке, что и данное состояние.

Смысл заключается в исследовании всех символов сразу. На 1 шаге разбиваем по принципу подобия (да/нет) На 2 и остальных происходит испытание всех блоков по одному входному символу (0,1) и их расщепление по признаку, где находиться преемник: в 1 и то же расщепление попадают состояния, имеющиеся в 1 и том же блоке => пока не прекращается расщепление блоков. Пр-е надо остановиться. И каждый из блоков будет содержать эквивалентные состояния.