Задание №4 Тема: Интерполирование математических таблиц.

Дана таблица значений функции с верными цифрами:

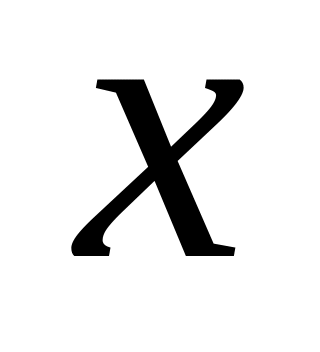
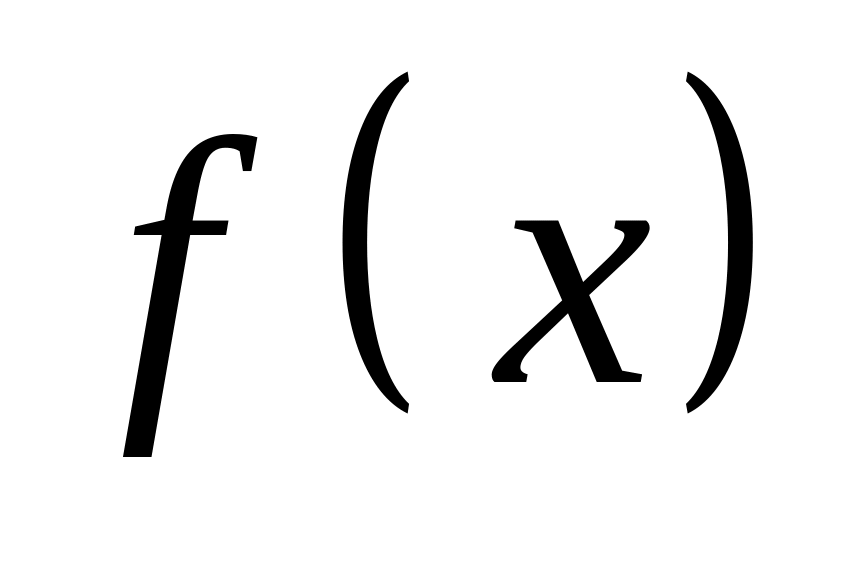
0	1	0,4	1,1024	0,8	1,5082	1,2	2,3881	1,6	3,9536
0,1	1,0053	0,5	1,1693	0,9	1,6763	1,3	2,7057	1,7	4,4823
0,2	1,0227	0,6	1,2575	1,0	1,8768	1,4	3,0696	1,8	5,0758
0,3	1,0543	0,7	1,3695	1,1	2,1130	1,5	3,4842	1,9	5,7396

1. Составьте программу, для вычисления приближенного значения функции в точках 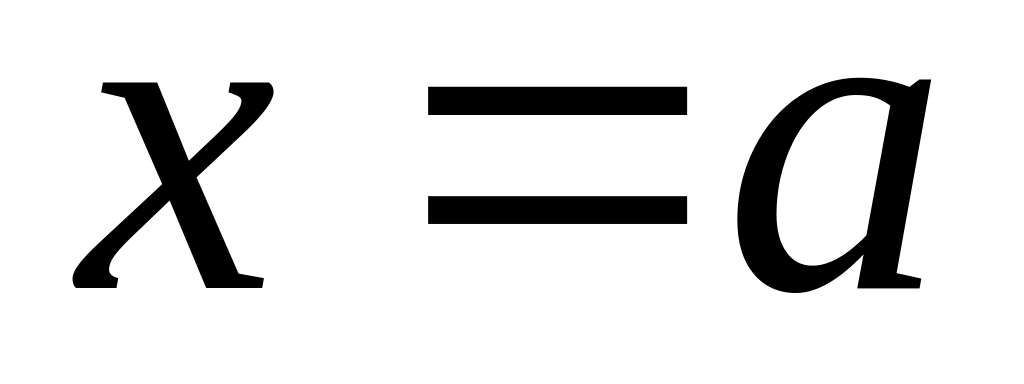, с помощью интерполяционного многочлена Лагранжа 5 степени. (Для достижения наилучшей точности выберите узлы, расположенные симметрично относительно заданного значения ).

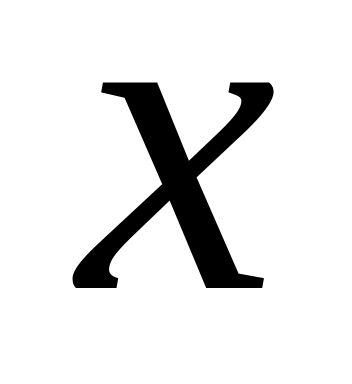2. Сравните полученное значение со значением функции, вычисленным по ее аналитическому выражению, заданному в таблице.

3. Определите абсолютную погрешность вычислений. Все исходные данные и числа считаются точными числами.

Данные по вариантам.

Вариант	1	2	3	4	5	6	7	8	9	10	11	12	13	14	15
	0,38	1,02	1,15	1,22	1,36	0,59	0,63	0,71	0,85	0,96	0,12	0,23	1,58	0,44	0,06
	0,35	1,07	1,18	1,24	1,31	0,54	0,68	0,75	0,83	0,92	0,18	0,26	1,55	0,47	0,02

Необходимые сведения из теории.

1. Табличная функция.

2. Задача интерполирования табличной функции.

3. Теорема о единственности задачи полиномиального интерполирования.

4. Интерполяционный многочлен Лагранжа.

5. Конечные разности таблиц.

6. Первый и второй интерполяционные многочлены Ньютона. Оценка погрешностей интерполяционных формул Ньютона.

Задание №5 Тема: Квадратичное приближение табличных функций по методу наименьших квадратов

По данной таблице постройте с помощью Excel точечный график и его линию тренда. Определите вид аппроксимирующей функции и найдите ее аналитическое выражение методом наименьших квадратов. Добавьте на исходный график полученной функции. Проанализируйте качество приближения. Найдите все уклонения от табличных значений и среднеквадратическое уклонение.

Вариант	Таблица
1	x 0,10 0,30 0,40 0,60 0,70 0,80 y 0,25 0,50 0,65 0,55 0,42 0,30
2	x -2,00 -1,80 -1,70 -1,60 -1,40 -1,30 y 5,10 4,00 3,20 3,90 4,80 6,10
3	x 1,30 1,40 1,60 1,70 2,00 2,10 y 2,40 1,80 1,20 1,40 2,30 2,90
4	x 0,40 0,70 0,90 1,10 1,40 1,60 y 0,15 0,83 1,65 1,52 0,90 0,31
5	x 2,00 2,50 2,70 2,90 3,20 3,40 y -0,11 -0,81 -1,05 -0,90 -0,23 -0,05
6	x -0,50 -0,30 -0,20 0,10 0,40 0,80 y 2,30 1,20 1,05 0,90 1,20 2,10
7	x 1,10 2,00 2,50 2,90 3,50 4,00 y 0,32 0,05 -0,10 -0,12 0,12 0,27
8	x 0,30 0,50 0,80 0,90 1,20 1,40 y 1,10 0,60 0,40 0,38 0,65 0,90
9	x -0,40 -0,10 0,10 0,20 0,50 0,70 y 1,30 3,50 4,20 4,00 2,80 1,60
10	x 1,20 1,40 1,50 1,60 1,80 2,10 y 0,90 3,30 4,10 3,90 2,80 1,10
11	x -0,90 -0,80 -0,50 -0,40 -0,20 -0,10 y 0,15 0,61 1,20 1,10 0,70 0,22
12	x -1,00 -0,80 -0,70 -0,40 -0,30 -0,20 y 1,40 0,90 0,65 0,51 0,78 1,30
13	x 0,20 0,30 0,50 0,70 0,90 1,20 y -2,10 -0,50 1,15 1,30 -0,60 -2,70
14	x 2,20 2,50 2,60 2,80 3,10 3,20 y 1,70 0,80 0,52 0,30 0,91 1,50
15	x -0,30 -0,10 0,20 0,30 0,70 0,90 y -2,10 1,30 3,00 2,40 -2,30 -8,00

Порядок выполнения работы

1. С помощью Excel на координатной плоскости постройте точки таблицы. Постройте линию тренда дающую наилучшее приближение.

2. Напишите в общем виде систему уравнений для определения коэффициентов аппроксимирующего многочлена и выражения для коэффициентов системы.

3. Составьте программу для нахождения аппроксимирующих функций (для вычисления коэффициентов решение системы необходимо определить по правилу Крамера).

4. Постройте график найденной функции на той же координатной плоскости, где отмечены точки таблицы.

5. Найдите все уклонения и среднеквадратическое уклонение от табличной функции.

Необходимые сведения из теории.

1. Задача аналитического приближения табличных функций.

2. Задача приближения по методу наименьших квадратов.

3. Алгоритм построения наилучшего многочлена по данному методу.

4. Уклонения, среднеквадратическое уклонение.