Свободные и связанные заряды.

При рассмотрении электростатического поля, в случае наличия в нем диэлектриков, нужно различать два рода электрических зарядов: свободные и связанные. Под свободными зарядами мы будем понимать, во-первых, все электрические заряды, которые под влиянием электрического поля могут перемещаться на макроскопические расстояния (электроны в металлах и вакууме, ионы в газах и электролитах и т. п.), и, во-вторых, заряды, нанесенные извне на поверхность диэлектриков и нарушающие их нейтральность ). Заряды же, входящие в состав нейтральных молекул диэлектриков, равно как и ионы, закрепленные в твердых диэлектриках вблизи определенных положений равновесия, мы будем называть зарядами связанными.

Потенциал ф электростатического поля при наличии в нем диэлектриков равен, очевидно, сумме потенциала (фо, возбуждаемого свободными зарядами, и потенциала (р', возбуждаемого связанными электрическими зарядами в диэлектриках:

Потенциал свободных зарядов определяется формулой (12.11):

где под р и а надо понимать объемную и поверхностную плотность свободных зарядов.

14

ПОЛЯРИЗАЦИИ ВЕКТОР (поляризация) - плотность электрич. дипольного момента среды, усреднённого по физически малому объёму. Причины возникновения поляризации сред разнообразны, напр. внеш. электрпч. поле (см. Поляризация среды), деформация (см. Пьезоэлектрики)и нагрев (см. Пироэлектрики ).Пространственное распределение П. в. однозначным образом определяет плотность связанного электрич. заряда В случае процессов, переменных во времени, наряду с П. в. вводится понятие тока поляризации Вектор поляризованности

Связь с электрическим полем

В основном зависимость между вектором поляризации и электрическим полем, которое обусловило поляризацию, линейна и задается тензором поляризуемости.

.

Определённые вещества могут быть поляризованными при отсутствии электрического поля. К таким веществам относятся пироэлектрики — кристаллические вещества со спонтанной поляризацией и электреты — аморфные вещества, в которых наведённая полем поляризация может сохраняться на протяжении длительного времени.

В случае переменного электрического поля среда может реагировать на изменение поля с некоторым запозданием. В этом случае вектор поляризации в данный момент зависит от напряжённости приложенного электрического поля в предыдущие моменты времени. В таких случаях говорят о временной дисперсии и соотношения между вектором поляризации и электромагнитным полем выглядят как

.

Фурье-образы вектора поляризации и напряжённости электрического поля в таком случае связаны линейным соотношением: , где

.

Если электромагнитное поле неоднородно в пространстве, как, например, в случае распространения электромагнитных волн, и взаимодействует с возбуждениями в веществе, которые имеют длину волны порядка длины электромагнитной волны, то значение поляризации в определенной точке пространства зависит от значения напряжённости электрического поля в соседних точках пространства. В таких случаях говорят о пространственной дисперсии (укр.)русск..

.

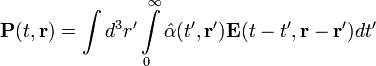В сильных электрических полях зависимость между поляризацией и электрическим полем может отличаться от линейной. Явления, которые при этом возникают изучаются, например, в нелинейной оптике.

15

Электрическое поле в диэлектрике. Рассмотрим плоский однородный диэлектрический слой, расположенный между двумя разноименно заряженными плоскостями (рис. 2.5). Пусть напряженность электрического поля, которое создается этими плоскостями в вакууме, равна ,

где - поверхностная плотность зарядов на пластинах (эти заряды называют свободными). Под действием поля диэлектрик поляризуется, и на его гранях появляются поляризационные или связанные заряды. Эти заряды создают в диэлектрике электрическое поле , которое направлено против внешнего поля .

,

где - поверхностная плотность связанных зарядов. Результирующее поле внутри диэлектрика

.

Поверхностная плотность связанных зарядов меньше плотности свободных зарядов, и не все поле E₀ компенсируется полем диэлектрика: часть линий напряженности проходит сквозь диэлектрик, другая часть обрывается на связанных зарядах (рис. 2.5). Вне диэлектрика . Следовательно, в результате поляризации поле внутри диэлектрика оказывается слабее, чем внешнее . Таким образом,

,

где - диэлектрическая проницаемость среды. Из формулы видно, что диэлектрическая проницаемость показывает, во сколько раз напряженность поля в вакууме больше напряженности поля в диэлектрике. Для вакуума , для диэлектриков .

16

Перейти к: навигация, поиск

Диэлектри́ческая восприи́мчивость (или поляризу́емость) вещества — физическая величина, мера способности вещества поляризоваться под действием электрического поля. Диэлектрическая восприимчивость  — коэффициент линейной связи между поляризацией диэлектрика P и внешним электрическим полем E в достаточно малых полях:

В системе СИ:

где  — электрическая постоянная; произведение называется в системе СИ абсолютной диэлектрической восприимчивостью.

В случае вакуума

У диэлектриков, как правило, диэлектрическая восприимчивость положительна. Диэлектрическая восприимчивость является безразмерной величиной.

Поляризуемость связана с диэлектрической проницаемостью ε соотношением:^[1]

(СГС)

(СИ)

ДИЭЛЕКТРИ́ЧЕСКАЯ ПРОНИЦА́ЕМОСТЬ, безразмерная величина , показывающая, во сколько раз сила взаимодействия F между электрическими зарядами в данной среде меньше их силы взаимодействия F_o в вакууме:

 F_о/F.

Диэлектрическая проницаемость показывает, во сколько раз поле ослабляется диэлектриком, количественно характеризуя свойство диэлектрика поляризоваться в электрическом поле.

Значение относительной диэлектрической проницаемости вещества, характеризующее степень его поляризуемости, определяется механизмами поляризации. Однако величина в большой мере зависит и от агрегатного состояния вещества, так как при переходах из одного состояния в другое существенно меняется плотность вещества, его вязкость и изотропность.

17

Имеем границу раздела двух сред с  и , так что,  (рис. 4.10, а).

а                                                      б

Рис. 4.10

      Как мы уже показали, в соответствии с (4.1.10),

 или ,

т.е.,  напряженность электростатического поля E изменяется скачком при переходе из одной среды в другую.

      Главная задача электростатики – расчет электрических полей, то есть  в различных электрических аппаратах, кабелях, конденсаторах, и т.д. Эти расчеты сами по себе не просты, да еще наличие разного сорта диэлектриков и проводников еще более усложняют задачу.

      Для упрощения расчетов была введена новая векторная величина – вектор электрического смещения (электрическая индукция):

(4.3.1)

      Из предыдущих рассуждений , тогда , отсюда

(4.3.2)

      Таким образом, вектор  остается неизменным при переходе из одной среды в другую (рис. 4.10, б), и это облегчает расчет . Зная  и ε, легко рассчитывать

, отсюда можно записать:

(4.3.3)

где  – вектор поляризации, χ – диэлектрическая восприимчивость среды, характеризующая поляризацию единичного объема среды.

      Таким образом, вектор  – есть сумма (линейная комбинация) двух векторов различной природы:  – главной характеристики поля и  – поляризации среды.

      В СГС:  поэтому в вакууме  и размерность у  и  одинакова.

      В СИ: , т. е. это заряд, протекающий через единицу поверхности.

      Для точечного заряда в вакууме

      Для  имеет место принцип суперпозиции, как и для , т.е.