Лабораторная работа № 5 Корреляционный анализ показателей эффективности работы предприятий

1. Цель работы

Получить практические навыки по применению корреляционного анализа показателей эффективности работы предприятий.

2. Общие сведения

2.1. Трехмерная модель. Основные параметры модели

Для изучения основных задач и особенностей корреляционного анализа удобно рассматривать генеральную совокупность трех при­знаков х, у и z.

Трехмерная нормально распределенная случайная вe­личина определяется девятью параметрами:

1. тремя математическими ожиданиями;

2. тремя дисперсиями (или средними квадратическими отклонениями);

3. тремя парными коэффициентами корреляции.

­Для трехмерной (и других многомерных) корреляционной модели важную­ роль играют частные и множественные коэффициенты корреляции или детерминации коэффициент детерминации равен квадрату соответствующего коэффициента корреляции).

Частным коэффициентом корреляции между х и у при фиксированных остальных компонентах (т,е. z) является выражение

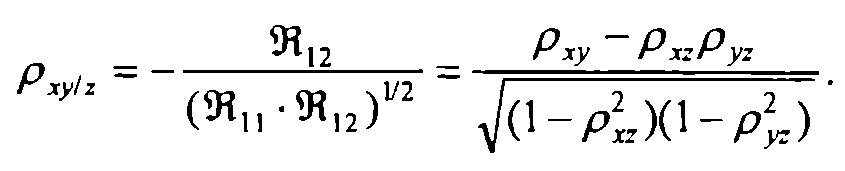
Остальные частные коэффициенты корреляции ρ_xz/y и ρ_yz/x определяют путем замены соответствующих индексов в приведенных формулах.

­Частный коэффициент корреляции обладает всеми свойствами парного коэффициента корреляции. Он служит показателем линейной связи между двумя переменными случайными величинами независимо от влияния остальных случайных переменных. Если частный коэффициент детерминации меньше, чем соответствующий парный коэффициент детерминации, то взаимоза­висимость между двумя величинами обусловлена частично (или цели­ком при равенстве нулю частного коэффициента детерминации) воз­действием на эту пару остальных, фиксируемых, случайных величин.

Множественный коэффициент корреляции между одной величиной z и двумя другими величинами (х,у) определяется по формуле:

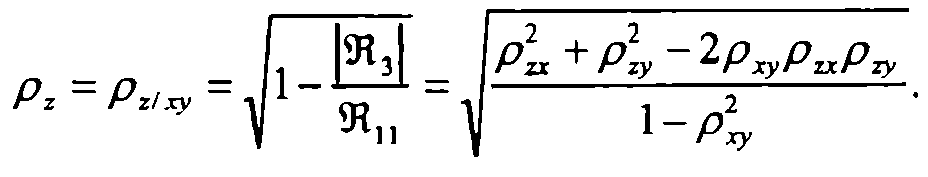
­Для трехмерной нормально распределенной случайной величины (x,y,z) множественный коэффициент корреляции является мерой связи между одной случайной величиной и двумя остальными. Он заключен между нулем и единицей.

При ρ_z= 1 связь между величинами z и (х,у) является функциональной, линейной: точки (x,y,z) расположены в плоскости регрессии z на (х,у). При ρ_z =0 одномерная случайная вели­чина z и двумерная случайная величина (х,у) являются независимыми (в силу нормальности распределения). Множественный коэффициент детерминации (ρ_z)² показывает долю дисперсии случайной величины z, обусловленную изменением случайных величин (х,у).

Проверка значимости множественного коэффициента детерминации (ρ_M)², (следовательно, и ρ_M) осуществляется с помощью F­-распределения.

2.2. Пример корреляционного анализа показателей эффективности работы предприятий

С целью анализа взаимосвязи показателей эффективности производства продукции: производительности труда, фондоотдачи и материалоемко­сти продукции была отобрана группа 25 однотипных машиностроительных предприятий.

На основании годовых отчетов предприятий были получены следую­щие данные (табл.5.1):

х - выработка валовой продукции в неизменных ценах на одного работающего средней списочной численности ППП (млн руб.);

у - выпуск валовой продукции на один рубль среднегодовой стоимости основных промышленно­производcтвенныx фондов (руб.);

z - материалоемкость в стоимостном выражении: стоимость материалов в валовой продукции в неизменных ценах (%).

Предположим, что рассматриваемые признаки х, у и z в rенераль­ной совокупности подчиняются нормальному закону распределения и указанные данные представляют выборку из этой совокупности.

Таблица 5.1 – Исходные данные

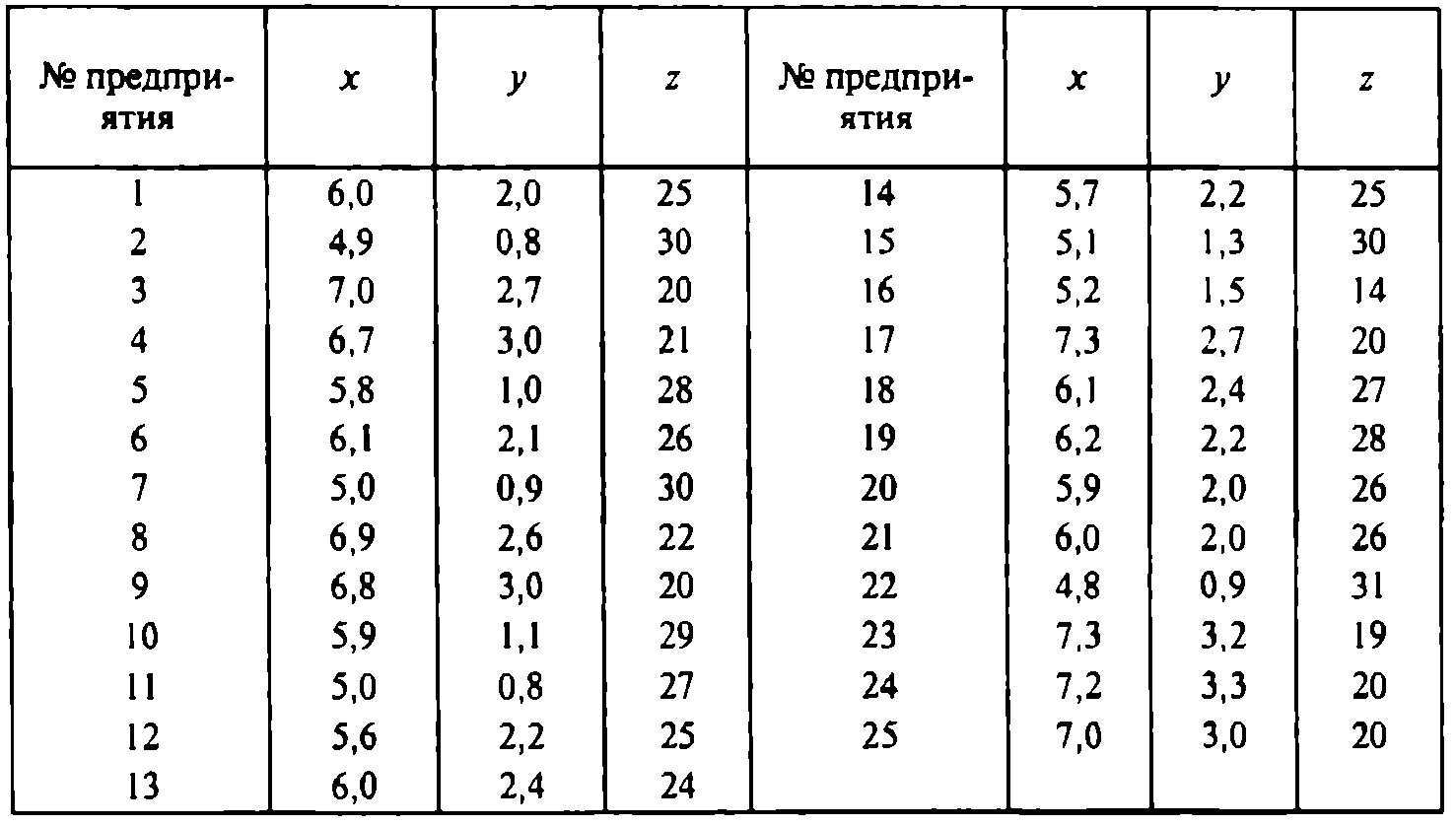
Для получения точечных оценок генеральных cpeдних, дисперсий средних квадратических отклонений и парных коэффициентов кoppeляции результаты промежуточных вычислений удобно поместить в расчетную таблицу (табл.5.2). С целью контроля вычислений данные разбиты на пятерки. Для каждой пятерки в итоговой (выделенной) строке приведены суммы элементов каждого столбца. В последнем контрольном столбце приводятся суммы элементов соответствующих строк. Сумма пяти элементов контрольного столбца должна совпадать с суммой элементов итоговой строки.

Таблица 5.2 – Расчетная таблица

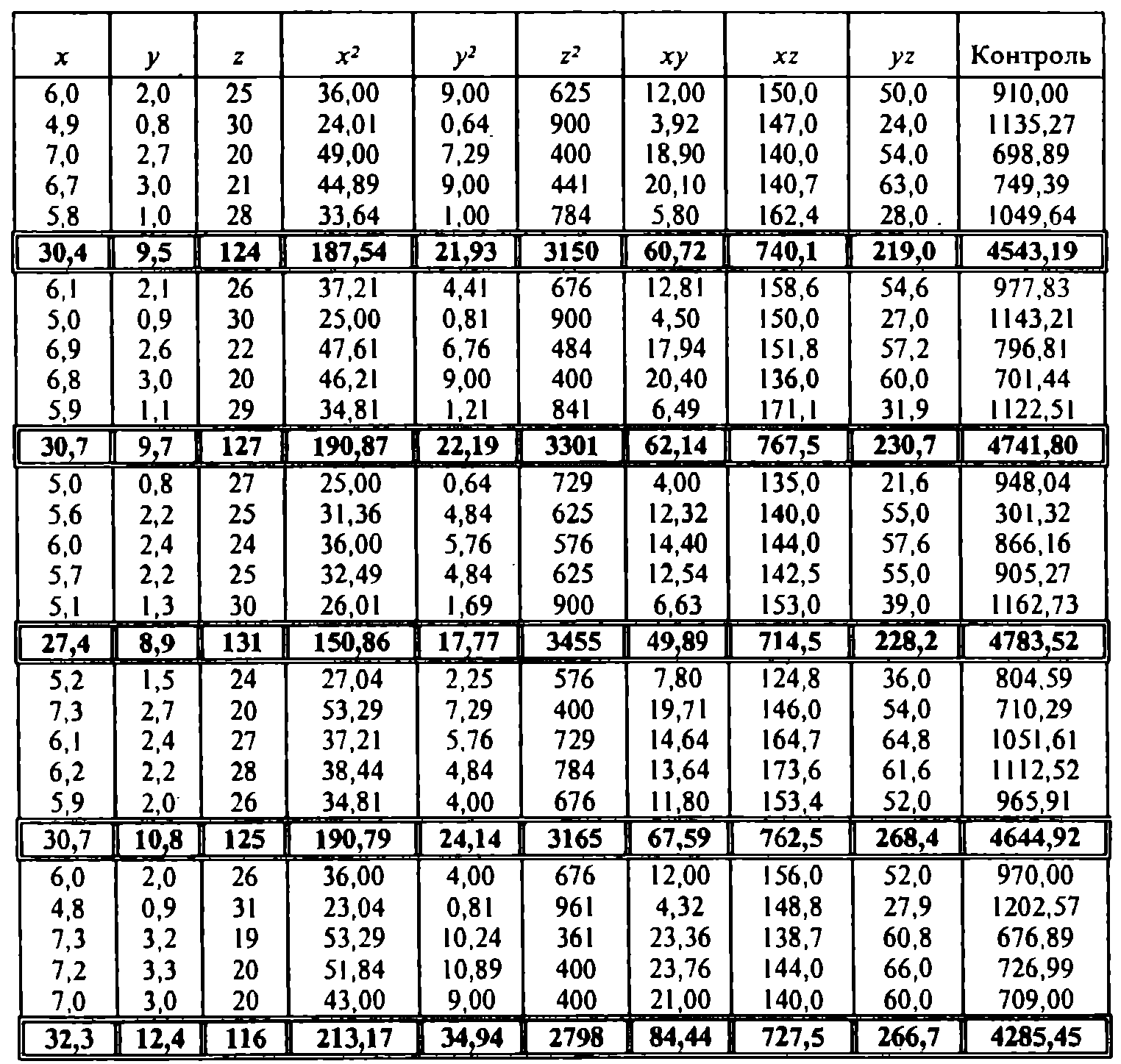
Например,

6,0+4,9+7,0+6,7+5,8=30,4;

6,0+2,0+25+ 36,0+9,0+625+ 12,0+ 150+50=91 0,0.

Контроль:

30,4+9,5+ 124+ 187.54+21,93+3150+60,72+740,1 +219,0=910,00+

+ 11,3527+698,89+749,39+ 1049,64=4543,19.

Далее получаем таблицу итоговых строк (табл. 5.3).

Таблица 5.3 – Итоговая таблица

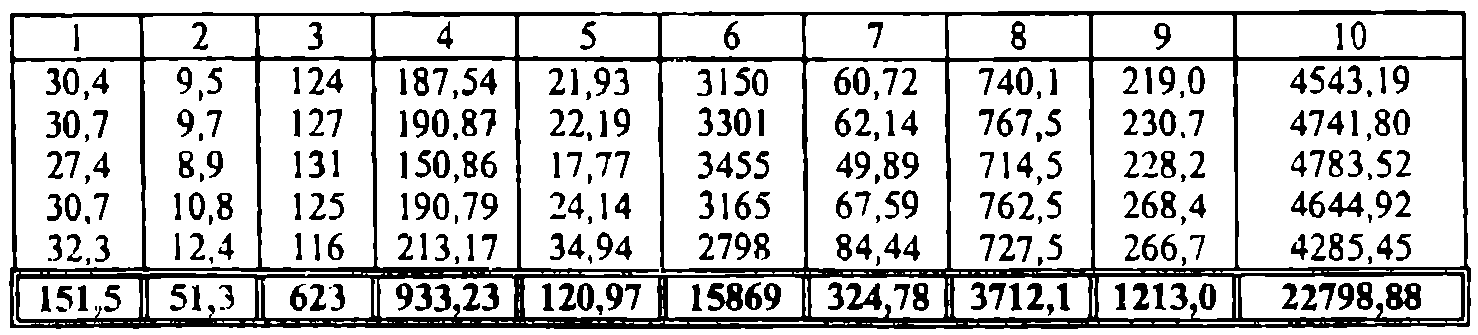
Из последней строки итоговой таблицы получаем

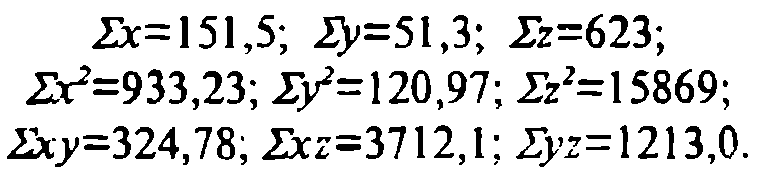
Следовательно,

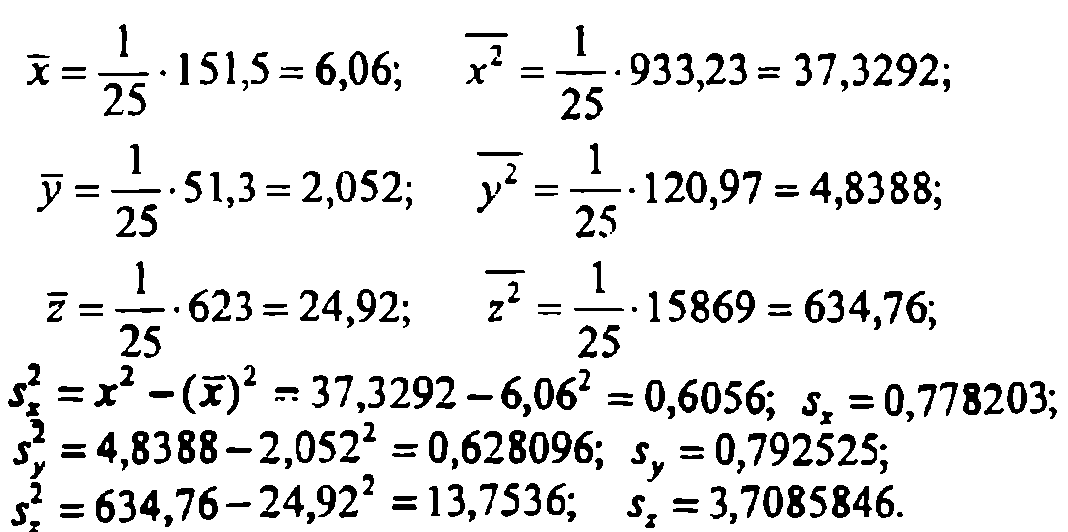
Для вычисления точечных оценок парных коэффициентов корреляции используем формулу

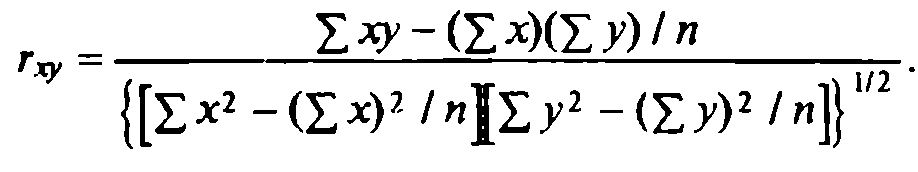
Получаем

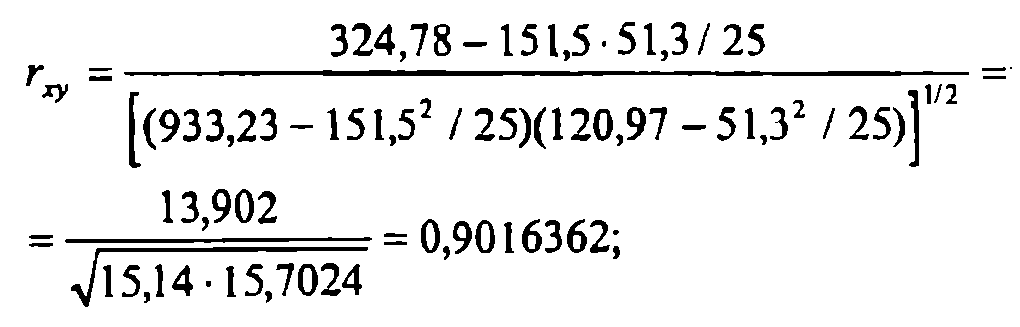
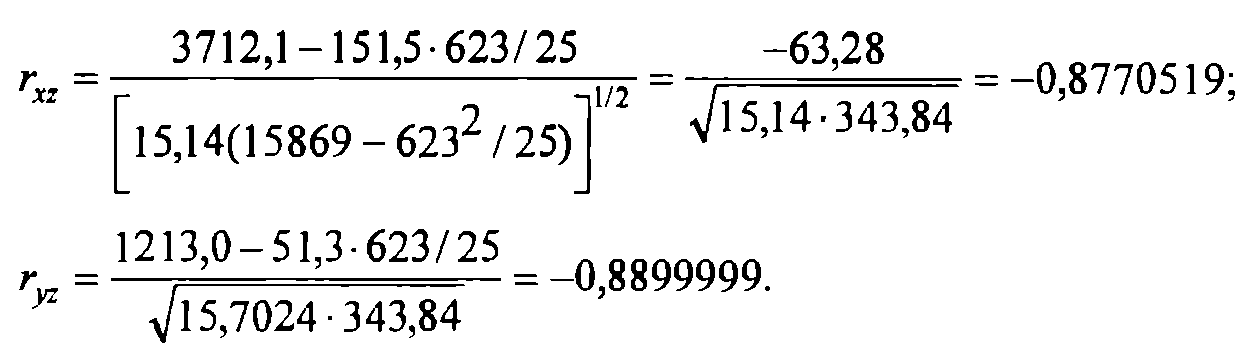
Вычисляем точечные оценки условных средних квадратических откло­нений (при фиксировании одной переменной):

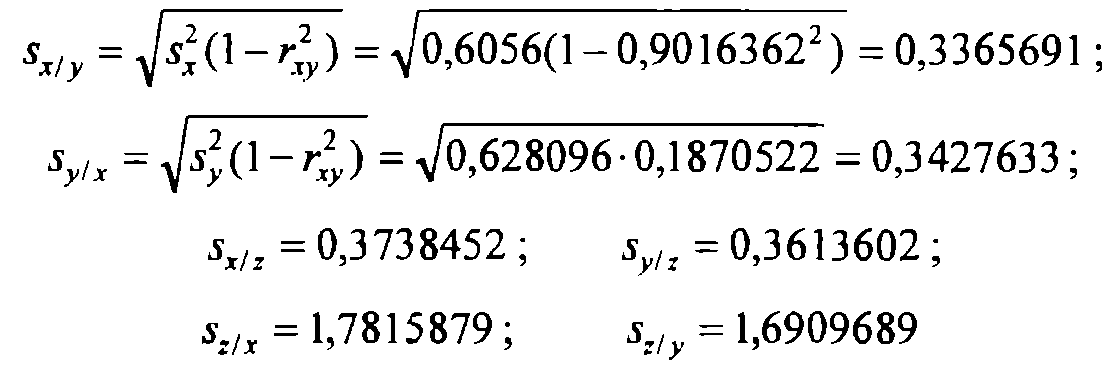
Получаем точечные оценки частных коэффициентов корреляции:

­

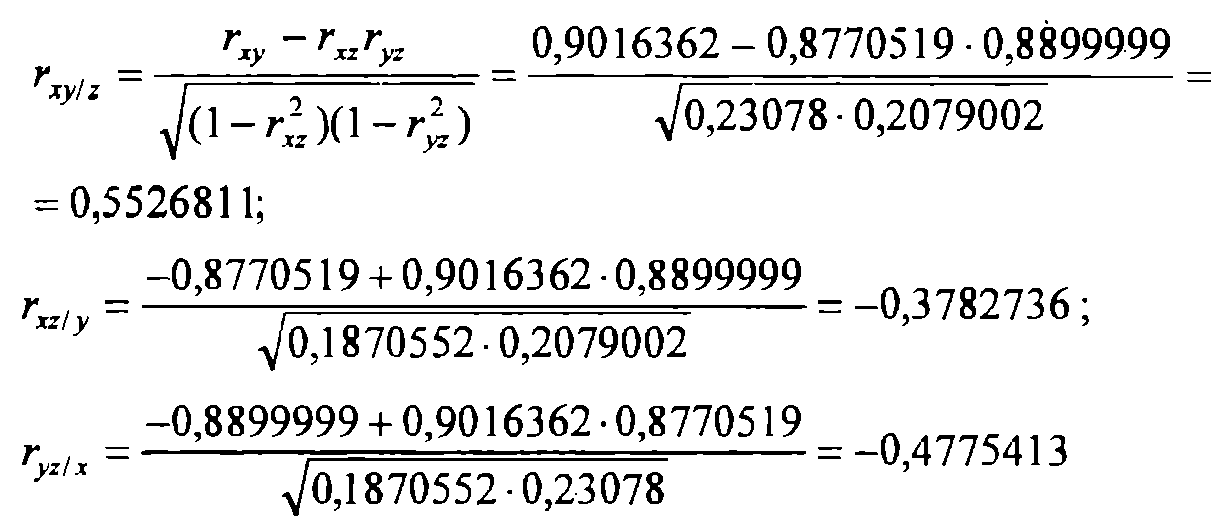
Вычисляем точечные оценки остаточных дисперсий (при фиксирова­нии двух переменных):

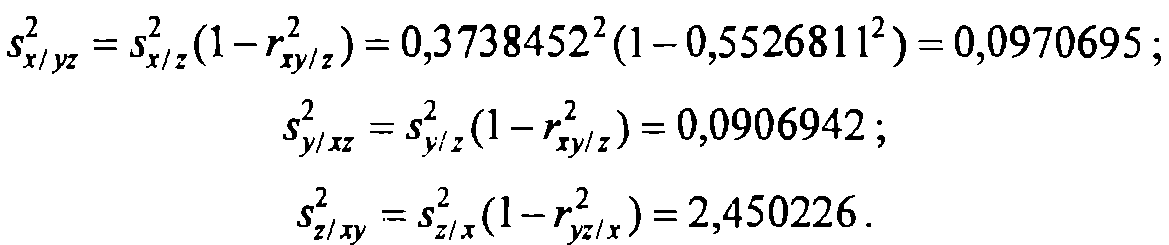
Получаем оценки множественных коэффициентов детерминации и корреляции:

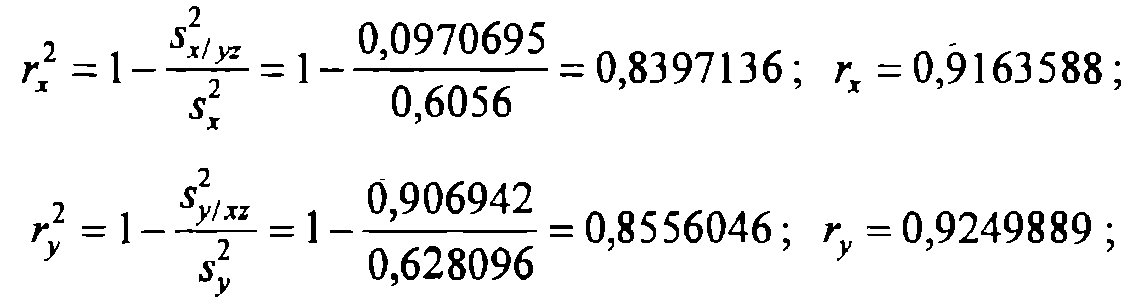
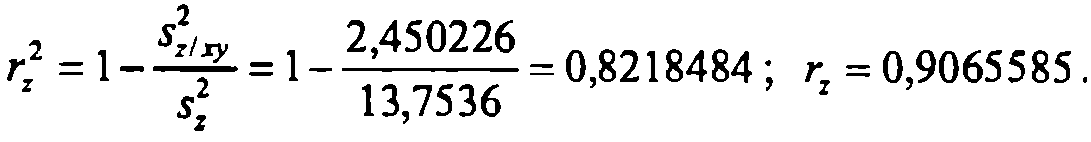
Для контроля вычислений полезно воспользоваться другими форму­лами точечных оценок множественных коэффициентов корреляции, нa­пример,

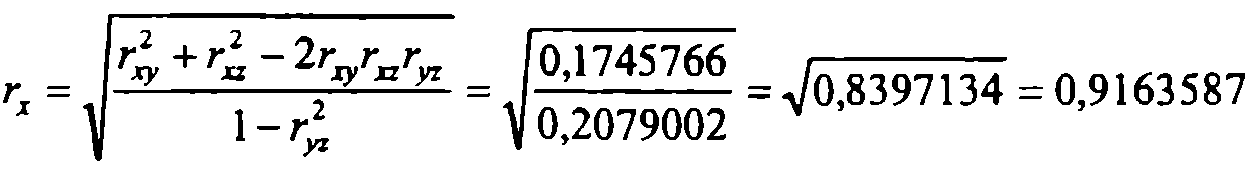
Ошибка в последнем разряде на единицу является допустимой. Проверим с уровнем α=0,05 значимость множественных коэффициен­тов корреляции. Вычислим наблюдаемые значения F­-критерия:

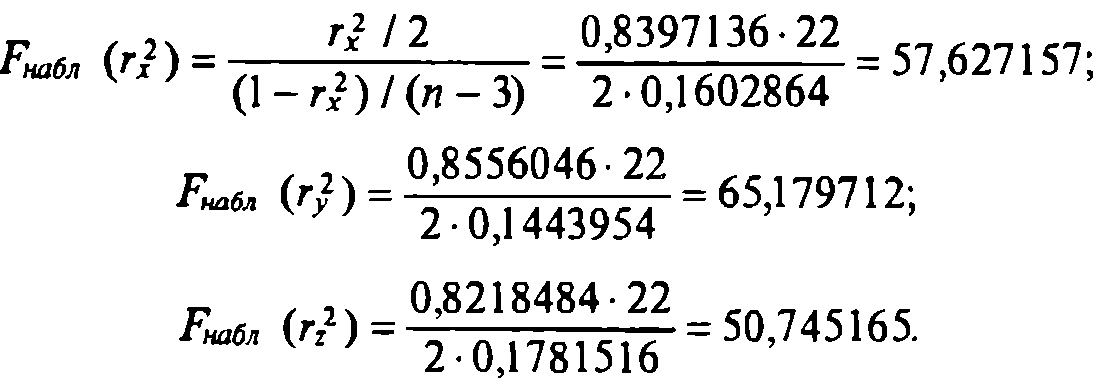
Находим, по таблице F­-распределения критическое значение F-статистик для уровня значимости α=0,05, числа степеней свободы числителя v1=2 и знаменателя v2=n­-3=22:

Так как все наблюдаемые значения F­-статистики превосходят ее критическое значение, то гипотеза о равенстве нулю каждого множественного коэффициента корреляции генеральной совокупности отвергается с вepo­ятностью ошибки, равной 0,05. Следовательно, эти коэффициенты значимо отличаются от нуля.

Проверим значимость частных коэффициентов корреляции с уровнем значимости α=0,05. По таблице распределения r-статистики для числа степеней свободы v=n­-3=22 и α=0,05 находим:

Или

Так как наблюдаемые значения больше 0,423, то они будут превосходить и Следовательно, гипотеза о равенстве нулю генеральных частных коэффициентов корреляции отвергается с вероятностью ошибки 0,05. Наблюдаемое значение r-статистики для частного коэффициента корреляции между х и у меньше 0,381, Т.е. и подавно меньше, чем . Следовательно, гипотеза не отвергается. Примем эту гипотезу, т.е. будем считать, что генеральный частный коэффициент корреляции между х и z равен нулю, т.е. незначим.

Итак, значимыми оказались только два частных коэффициента кoppe­ляции Заметим, что в случае необходимости можно было бы вычислить , например, с помощью линейной интерполяции:

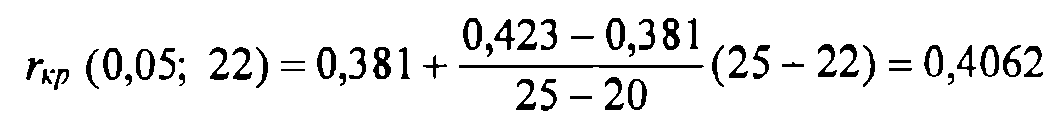
С надежностью γ=1­-α =0,95 найдем интервальные оценки значимых частных коэффициентов корреляции.

Для получаем по таблице функции ­ значение Z_0,55=0,6184. Затем вычисляем точность интервальной оценки для МZ:

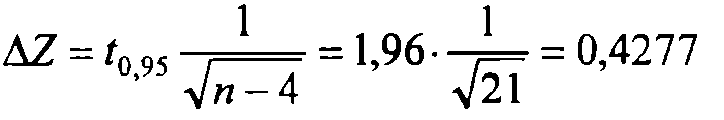
(t_0,95 находится по таблице интеграла Лаплaса). Интервальная оценка для МZ есть:

Или

Чтобы получить интервальную оценку для по таблицам Z_r нaxoдим числа, ближайшие к 0,1907 и к 1,0461. Это будут числа Z_rmin= 0,1923 и Z_rmax = 1,0454. Переходя к apгyмeнтy r, получим

Для будем иметь Z­_-0,48=-Z_0,48=­-0,5230. Тогда

­

или

­

Ближайшими к числам 0,0953 и 0,9507 будут 0,1003 и 0,9505. Следова­тельно, интервальная оценка для есть

Для изучаемых трех признаков нет односторонней причинно­-следственной связи. Поэтому выберем в качестве модели взаимозависимости статистически наиболее надежную в условиях данной выборки. Значимым множественным коэффициентом детерминации, имеющим наибольшую оценку является . Ему соответствуют оба значимых частных коэффициента детерминации (имеющих и оценки больше, чем oцeнка ).

­Оценка соответствующе его уравнения регрессии имеет вид

Вычислим коэффициенты множественной (частной) регрессии:

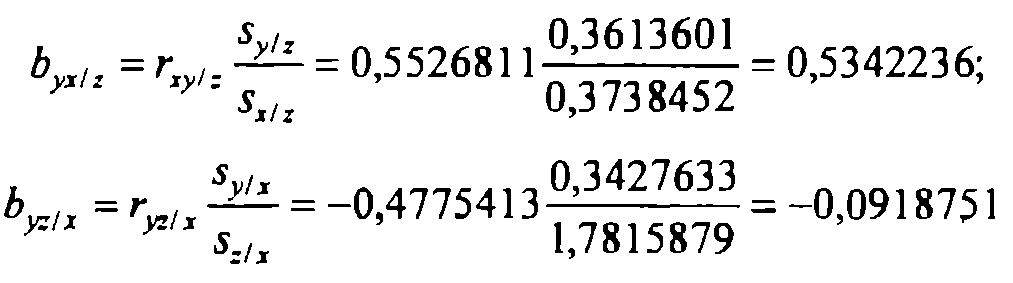
Таким образом, получаем

­

­Найдем с надежностью γ=1­-α =0,95 интервальные оценки для множественных коэффициентов регрессии. По таблице распределения Стьюдента находим t(α,n­-3)=t(0,05; 22)=2,074 и решим относительно β неравенства

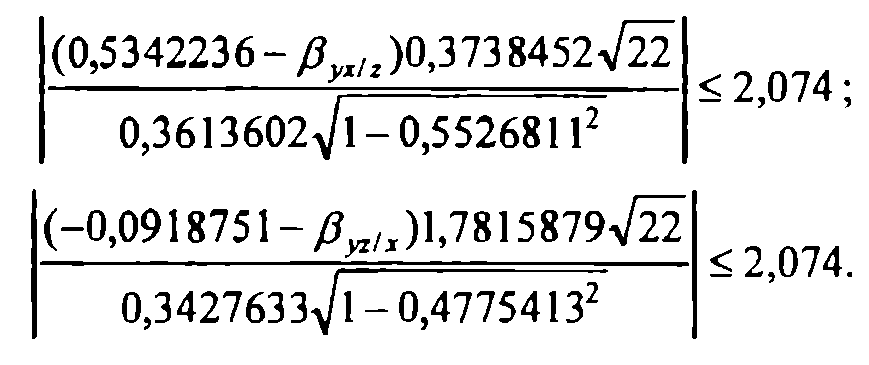
Вычислим точности интервальных оценок:

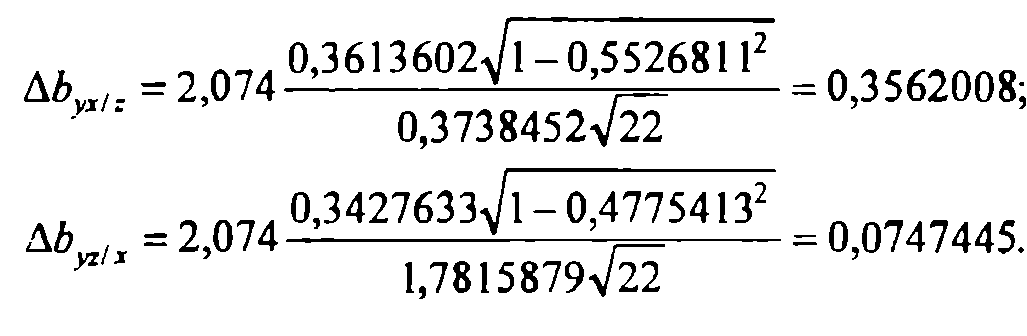
Откуда

­

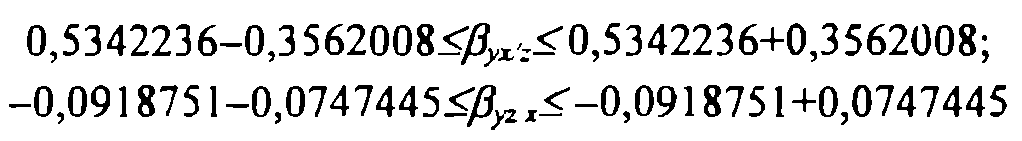
или

­

Получим предпочтительные точечные оценки изучаемых коэффици­ентов детерминации:

На основании полученных расчетов можно сделать следующие вы­воды.

Доказана тесная взаимосвязь каждого из исследуемых показателей эффективности работы предприятия с другими (все множественные коэффициенты детерминации значимы и превышают 0,8).

Особенно тесная связь существует между фондоотдачей и двумя oc­тальными показателями ­ производительностью труда и материалоем­костью. Изменение фондоотдачи в среднем на 84,25% объясняется изме­нением производительности труда и материалоемкости (изменение фон­доотдачи в среднем на 15,75% объясняется влиянием неконтролируемых факторов, признаков). При этом при увеличении производительности труда на 1 млн руб. фондоотдача увеличивается в среднем на 0,55 руб. на рубль основных производственных фондов. При уменьшении материало­емкости на 1 % фондоотдача увеличивается в среднем на 0,48%. Указанные нормативы относительно стабильны при условии, что изучаемые показа­тели отклоняются на небольшие величины от своих средних уровней (стабильность указывается доверительными интервалами и вероятностью 0,95). Взаимозависимость между материалоемкостью и производительностью труда (без учета фондоотдачи) не доказана (частный коэффициент корреляции незначим) при данных условиях. Для более надежной проверки такой зависимости необходим большой объем выборки.